我们知道。一个正方形可以剪成4个小正方形，那么一个正方形能否剪成9个正方形，能否剪成11个正方形(大小不一定要相同)?( )A．前者能、后者不能B．前者不能、后者能C．两者都不能D．两者都能

第1题：

劳动技能课上老师给出一道手工题：一张正方形纸片，在一对对角处各减去一个边长为1厘米的小正方形（如右图所示），想办法把这个缺角的正方形恰好剪成一些长2厘米、宽1厘米的小矩形，问初始的大正方形边长要多大时，任务才有可能完成

A.8厘米
B.15厘米
C.32厘米
D.以上答案都不对

答案：D

解析：

第一步，本题考查几何问题中的几何构造。第二步，首先排除B选项15，15×15＝225，去除两个角为223，不能被2整除，所以排除；再验证剩余偶数选项，以4×4为例，标数如下图，发现被拿掉的为1和13，不管n×n，拿去的两个位置奇偶性一定相同，所以拿去的数字之和为偶数，再看剩余，要2×1的长方形，一定是挨着的两个正方形组成，挨着的两个正方形奇偶性不同，加和为奇数，验证8×8，总共64个格，去除两个角还剩62个，可组成31个2×1的长方形，每个和都是奇数，所以奇数×31还是奇数，加上两个角的偶数应该为奇数，但是1＋2＋3＋……＋63＋64为偶数，不满足，同理32×32也不满足。



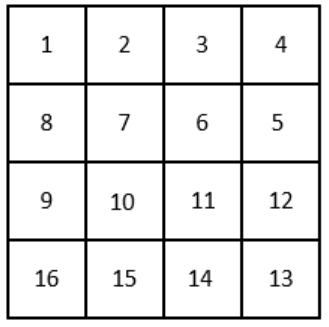
第三步，A、B、C选项都不满足，因此以上答案都不对。因此，选择D选项。

第2题：

第3题：

【单选题】下列程序运行后得到的图形是（）。 [x,y]=meshgrid（-2:2); z=x+y; i=find（abs（x)＜1 & abs（y)＜1); z（i)=NaN; surf（x,y,z);shading interp

A．在一个正方形的正中心挖掉了一个小的正方形

B．在一个正方形的正中心挖掉了一个小的长方形

C．在一个正方形的上端挖掉了一个小的正方形

D．在一个正方形的下端挖掉了一个小的正方形

第4题：

劳动技能课上老师给出一道手工题：一张正方形纸片，在一对对角处各减去一个边长为1厘米的小正方形（如右图所示），想办法把这个缺角的正方形恰好剪成一些长2厘米、宽1厘米的小矩形，问初始的大正方形边长要多大时，任务才有可能完成？

A.8
B.15
C.32
D.以上答案都不对

答案：D

解析：

将大正方形拆分为若干个边长 1 厘米的小正方形，根据大正方形边长的奇偶性分类讨论如下：
①若大正方形的边长为奇数，则小正方形的个数也为奇数，剪去 2 个小正方形后，剩下的小正方形个数依
然为奇数；而每个小矩形需要占用 2 个小正方形，则剩下的奇数个小正方形不可能全部拆成小矩形，矛盾。故 边长为奇数必然不满足题意，排除 B 项；
②若大正方形的边长为偶数，如下图所示：将其拆分为若干个小正方形之后，黑色和白色方块的总数相等， 且拿掉的对角的两个小正方形一定都是黑色或白色，那么剩下的黑色与白色方块数必然不等，此为结论 1。
观察图形，要取出 2×1 的小矩形，必须由一黑一白组成。那么，要让剩下的图形恰好能分成若干个 2×1 的小矩形，则剩下图形的黑色与白色方块个数必须相等，此为结论 2。
结论 2 与结论 1 明显矛盾，故边长为偶数也必须不满足题意，排除 A、C 项。 故正确答案为 D。

第5题：

下列程序运行后得到的图形是（）。 [x,y]=meshgrid（-2:2); z=x+y; i=find（abs（x)＜1 & abs（y)＜1); z（i)=NaN; surf（x,y,z);shading interp

A．在一个正方形的正中心挖掉了一个小的正方形

B．在一个正方形的正中心挖掉了一个小的长方形

C．在一个正方形的上端挖掉了一个小的正方形

D．在一个正方形的下端挖掉了一个小的正方形