将一个正方形分成9个小正方形，填上1到9这9个自然数，使得任意一个横行，一个纵列以及每一对角线上的3个数之和等于15，请问位于中间的小正方形理应填哪个数?A .4 B .5 C .6 D.7
题目
将一个正方形分成9个小正方形，填上1到9这9个自然数，使得任意一个横行，一个纵列以及每一对角线上的3个数之和等于15，请问位于中间的小正方形理应填哪个数?
A .4 B .5 C .6 D.7
相似考题
更多“将一个正方形分成9个小正方形,填上1到9这9个自然数,使得任意一个横行,一个纵列以及每一对角线 ”相关问题
-
第1题：
如图，将正方形边长三等分后可得9个边长相等的小正方形，把中间的小正方形去掉，对剩下的8个小正方形，均按上面方法操作。问：对一个边长为2的正方形如此操作三次后所剩白色区域的面积是多少？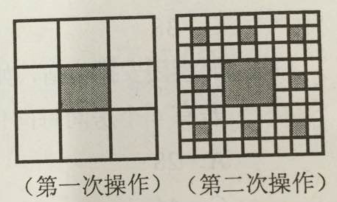
A.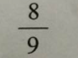
B.
C.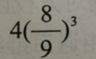
D.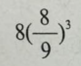
答案：C解析：
-
第2题：
由20×20的小方格组成一个大正方形，从1~9这9个数字中任意选出一个数字填入每个小方格。把其中任意一个田字格图形中的4个数相加，均能得到一个和数。请问所能得到的和数中，至少有（ ）个是相同的。A.11
B.20
C.33
D.36答案：A解析：第一步，本题考查最值问题，用极值思维解题。
第二步，1~9中4个数相加的和数中最小为1+1+1+1=4，最大为9+9+9+9=36，中间每一个都可以取到，则和数的总数为36－4＋1=33（个）。
第三步，20×20的小方格可以组成（20－1）×（20－1）=19×19=361（个）田字方格。
第三步，要使相同和数个数尽量少，则每个和数应尽可能的多，最多的情况为个数都相同，则为
则至少有10＋1=11（个）是相同的。 -
第3题：
【单选题】下列程序运行后得到的图形是（）。 [x,y]=meshgrid（-2:2); z=x+y; i=find（abs（x)＜1 & abs（y)＜1); z（i)=NaN; surf（x,y,z);shading interp
A．在一个正方形的正中心挖掉了一个小的正方形
B．在一个正方形的正中心挖掉了一个小的长方形
C．在一个正方形的上端挖掉了一个小的正方形
D．在一个正方形的下端挖掉了一个小的正方形
在一个正方形的正中心挖掉了一个小的正方形 -
第4题：
将一个正方形分成9个小正方形，填上1到9这9个自然数，使得任意一个横行，一个纵列以及每一对角线上的3个数之和等于15，请问位于中间的小正方形应填哪个数?
A. 4
B. 5
C. 6
D. 7答案：B解析：解题指导： 欲保证3个数之和都等于15，只有中间的数字为平均数5才可。故答案为B。 -
第5题：
下列程序运行后得到的图形是（）。 [x,y]=meshgrid（-2:2); z=x+y; i=find（abs（x)＜1 & abs（y)＜1); z（i)=NaN; surf（x,y,z);shading interp
A．在一个正方形的正中心挖掉了一个小的正方形
B．在一个正方形的正中心挖掉了一个小的长方形
C．在一个正方形的上端挖掉了一个小的正方形
D．在一个正方形的下端挖掉了一个小的正方形
在一个正方形的正中心挖掉了一个小的正方形