在右图小空格中已填上了1及7两个自然数，如果其他空格也填上相应不同的数，使得任意一个横行、任意一个纵列以及任意一条对角线上的3个数之和都等于111 。请问，位于中间的小正方形里应填的数是：A61 B53 C41 D3

题目
在右图小空格中已填上了1及7两个自然数，如果其他空格也填上相应不同的数，使得任意一个横行、任意一个纵列以及任意一条对角线上的3个数之和都等于111 。请问，位于中间的小正方形里应填的数是：

A61
B53
C41
D3

相似考题

1.任意两个自然数中一定有一个是奇数。（ ）

2.（ 14 ）输入掩码字符 “ ＆ ” 的含义是A ）必须输入字母或数字B ）可以选择输入字母或数字C ）必须输入一个任意的字符或一个空格D ）可以选择输入任意的字符或一个空格

3.● 现需要将数字2和7分别填入6个空格中的2个（每个空格只能填入一个数字），已知第1格和第2格不能填7，第6格不能填2，则共有 （63） 种填法。（63）A. 12B. 16C. 17D. 20

4.将一个正方形分成9个小正方形，填上1到9这9个自然数，使得任意一个横行，一个纵列以及每一对角线上的3个数之和等于15，请问位于中间的小正方形理应填哪个数?A .4 B .5 C .6 D.7

更多“在右图小空格中已填上了1及7两个自然数，如果其他空格也填上相应不同的数，使得任意一个横行、任意一个纵列以及任意一条对角线上的3个数之和都等于111 。请问，位于中间的小正方形里应填的数是： ”相关问题

  • 第1题：

    在Excel里面使用查找功能时,如果要使用模糊查找,要在查找的目标内容后加一个任意通配符,请问任意通配符具体指哪个符号?()

    A.星号

    B.井号

    C.空格

    D.冒号


    正确答案:A

  • 第2题：

    一个正方体木块放在桌子上，每一面都有一个数，位于对面上的两个数之和都等于14，小张能看到顶面和两个侧面，看到的三个数之和是18；小李能看到顶面和另外两个侧面，看到的三个数之和是24，那么贴着桌子这个面的数是()．

    A．6

    B．8

    C．3

    D．7


    正确答案：D
    D[解析]小张和小李看到的正方体面上的数字相加，就是完整的四个侧面数字和两次顶面数字之和，因为正方体两个对面的两个数之和等于14，那么四个侧面的数字和应为 14×2=28，由此可知顶面数字为(18+24-28)÷2=7，那么贴着桌子的这一面的数就是14-7=7．

  • 第3题：

    Word录入原则是()。

    A.可任意加空格、回车键;

    B.可任意加空格、不可任意加回车键;

    C.不可任意加空格、回车键

    D.不可任意加空格,可任意加回车键;


    正确答案：C

  • 第4题：

    有4个不同的自然数，它们当中任意两数的和是2的倍数；任意3个数的和是3的倍数，为了使得这4个数的和尽可能小，则这四个数的和为（ ）。

    A. 40
    B. 42
    C. 46
    D. 51

    答案：A
    解析：
    任意两个数的和是2的倍数，所以这些数的奇偶性相同。任意三个数的和是3的倍数，所以这些数除以3，所得余数必定相同（否则在三个数的和中换一个数，和将不是3的倍数）。于是， 这些数除以6所得余数相同，故这最小的四个数为1，7，13，19。所以这四个数的和为1 + 7 + 13 + 19 = 40。

  • 第5题：

    现有20个均不等于7的正整数排成一行，其中，任意连续若干个数的和也不等于7，则这20个数之和的最小值为_______。


    答案：
    解析：
    34。解析：本题考查了一个基本结论：n个正整数排成一行，则必定可以找到其中连续若干个数的和是n的倍数。运用这一结论，则对排成一行的7个正整数而言，必定可以找到连续若干个数的和是7的倍数，如果要求任意连续若干个数的和不等于7，则前述“7的倍数”最小就是l4，此时这7个数是六个1和1个8。对于排成一行的20个正整数而言，任意连续若干个数的和不等于7，它们的和最小的情况是：1，1，1，1，1，1，8，1，1，1，1，1，1，8，1，1，1，1。此时它们的和为34。

  • 第6题：

    将一个正方形分成9个小正方形，填上1到9这9个自然数，使得任意一个横行，一个纵列以及每一对角线上的3个数之和等于15，请问位于中间的小正方形应填哪个数?


    A. 4
    B. 5
    C. 6
    D. 7

    答案：B
    解析：
    解题指导： 欲保证3个数之和都等于15，只有中间的数字为平均数5才可。故答案为B。

  • 第7题：

    由20×20的小方格组成一个大正方形，从1~9这9个数字中任意选出一个数字填入每个小方格。把其中任意一个田字格图形中的4个数相加，均能得到一个和数。请问所能得到的和数中，至少有（ ）个是相同的。

    A.11
    B.20
    C.33
    D.36

    答案：A
    解析：
    第一步，本题考查最值问题，用极值思维解题。
    第二步，1~9中4个数相加的和数中最小为1+1+1+1=4，最大为9+9+9+9=36，中间每一个都可以取到，则和数的总数为36－4＋1=33（个）。
    第三步，20×20的小方格可以组成（20－1）×（20－1）=19×19=361（个）田字方格。
    第三步，要使相同和数个数尽量少，则每个和数应尽可能的多，最多的情况为个数都相同，则为

    则至少有10＋1=11（个）是相同的。

  • 第8题：

    在1和2015之间（包括1和2015在内）不能被4、5、6三个数任意一个数整除的数有（）个。


    正确答案:1075

  • 第9题：

    帕斯卡三角里面，任意一条对角线上相邻两个数的比等于各自往两边数的单元的个数之比。


    正确答案:正确

  • 第10题：

    输入掩码字符“&”的含义是（）

    • A、必须输入字母或数字
    • B、可以选择输入字母或数字
    • C、必须输入一个任意的字符或一个空格
    • D、可以选择输入任意的字符或一个空格

    正确答案:C

  • 第11题：

    单选题
    Word中字符数据的录入原则是（）。
    A

    可任意加空格、回车键

    B

    可任意加空格、但不可以任意加回车键

    C

    不可任意加空格、回车键

    D

    不可任意加空格、但可以任意加回车键


    正确答案： A
    解析： 暂无解析

  • 第12题：

    单选题
    有4个不同的自然数，他们当中任意两数的和是2的倍数，任意3个数的和是3的倍数，为了使这4个数的和尽可能小，则这4个数的和为（）
    A

    40

    B

    42

    C

    46

    D

    51


    正确答案： D
    解析： 暂无解析

  • 第13题：

    有四个不同的正整数，其中任意两个数之和是2的倍数，任意三个数的和是3的倍数，满足条件的最小的四个正整数之和是：

    A．51

    B．38

    C．40

    D．42


    正确答案：C
    首先这4个数必须同奇偶，其次这4个数必须对于3同余则4个数必须对6同余；又要最小则4个数中最小的是1，所以1、7、13、19是满足条件的最小的四个正整数，和为40。

  • 第14题：

    有5个不同的自然数，它们当中任意3个的和是3的倍数，任意4个的和是4的倍数，那么满足以上条件的5个数的和最小是（ ）。

    A．96

    B．108

    C．116

    D．125


    正确答案：D
    5个不同的自然数，它们当中任意3个数的和是3的倍数，说明这5个自然数被3除，余数相同；5个不同的自然数，它们当中任意4个数的和是4的倍数，说明这5个自然数被4除，余数相同，因此，这5个数被3×4=12除，余数也相同，为了使这5个数的和最小，余数取1，则这5个数为1+12×0=1，1+12×1=13，1+12×2=25，1+12×3=37，1+12×4—49，1+13+25+37+49=125。本题正确答案为D。

  • 第15题：

    ●自然数1，2，3，4，5中，任意两个数都可以算出平均值，其中有些平均值是相同的。那么，不同的平均值共有 (28) 个。

    (28)

    A．4

    B．7

    C．8

    D．9


    正确答案：B

  • 第16题：

    1～100，这100个自然数中，最多可以选出多少个数，才能保证任意两个数之和都不能被3整除？（）

    A.33
    B.34
    C.35
    D.36

    答案：C
    解析：
    这100个数可以分成三类：①能被3整除的数，共有33个；②被3除余数是1的数，共有34个；③被3除余数是2的数，共有33个。显然，把第②组的数全选出，再从第①组任选一个数，保证任两个数字之和不能被3整除，即最多可以选出34＋1＝35个，故本题选C。

  • 第17题：

    阅读以下说明和流程图，填写流程图中的空缺，将解答填入答题纸的对应栏内。【说明】如果一个自然数N恰好等于它所有不同的真因子（即N的约数以及1，但不包括N）之和S，则称该数为“完美数”。例如6＝1＋2＋3，28＝1＋2＋4＋7＋14，所以6和28都是完美数。显然，6是第1个（即最小的）完美数。下面流程图的功能是求500以内所有的完美数。【流程图】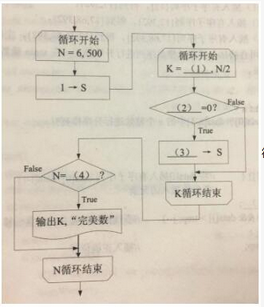

    循环开始框中要注明：循环变量＝初始值，终值［，步长］，步长为1时可以缺省。如果某自然数小于其所有真因子之和（例如24＜1＋2＋3＋4＋6＋8＋12），则称该自然数为亏数；如果某自然数大于其所有真因子之和（例如8＞1＋2＋4），则称该自然数为贏数；如果某自然数等于从1开始的若干个连续自然数之和（例如10＝1＋2＋3＋4）则称该自然数为三角形数。据此定义，自然数496是（ ）。供选择答案：A.亏数 B.赢数 C.完美数，非三角形数 D.完美数和三角形数


    答案：
    解析：
    （1）2（2）N%K（3）S+K（4）S（5）D
    【解析】

    流程图的功能是求500以内所有的完美数，N的值范围是6~500，因此N是需要判断是否为完美数，首先需要求出N的所有真因子，然后再判断N和真因子之和是否相等，从流程图可以看出S是保存真因子和的变量，K是保存真因子的变量，因此K的初始值是2，终值是N/2，因此第（1）空处填写：2；判断K是否为N的真因子，即判断N%K（N除以K取余）是否为0，第（2）空填写：N%K；当K为N的真因子时，需要计算所有K的和，即S=S+K，第（3）空填写：S+K；最后判断N和S是否相等，第（4）空填写：S。496的真因子有：1、2、4、8、16、31、62、124、248，1+2+4+8+16+31+62+124+248=496；因此496是完美数，同时496=（1+2+3+4+……+30+31），因此496是完美数和三角形数。

  • 第18题：

    有4个不同的自然数，它们当中任意两数的和是2的倍数；任意3个数的和是3的倍数，为了使得这4个数的和尽可能小，则这四个数的和为（　　）。
    A.40
    B.42
    C.46
    D.51


    答案：A
    解析：
    任意两个数的和是2的倍数，所以这些数的奇偶性相同；任意三个数的和是3的倍数，所以这些数除以3，所得余数必定相同(否则在三个数的和中换一个数，和将不是3的倍数)。于是这些数除以6所得余数相同，故这最小的四个数为1、7、13、19。所以这四个数的和为1+7+13+19=40。

  • 第19题：

    现需要将数字2和7分别填入6个空格中的2个（每个空格只能填入一个数字），已知第1格和第2格不能填7，第6格不能填2，则共有（）种填法。

    • A、12
    • B、16
    • C、17
    • D、20

    正确答案:C

  • 第20题：

    如果一个数列中数的个数为偶数，中位数是位于最中间的两个数的（）


    正确答案:平均数

  • 第21题：

    在CCED下编辑屏幕的标尺行最左端的数字，允许使用的范围是（）。

    • A、任意数
    • B、任意一位数
    • C、1-4中的一个整数
    • D、1-4中的一个数

    正确答案:C

  • 第22题：

    Word中字符数据的录入原则是（）。

    • A、可任意加空格、回车键
    • B、可任意加空格、但不可以任意加回车键
    • C、不可任意加空格、回车键
    • D、不可任意加空格、但可以任意加回车键

    正确答案:A

  • 第23题：

    判断题
    帕斯卡三角里面，任意一条对角线上相邻两个数的比等于各自往两边数的单元的个数之比。
    A

    对

    B

    错


    正确答案： 错
    解析： 暂无解析

相关内容