有分别写着1,2,3,…,13的卡片各两张,任意抽出两张,计算这两张卡片上的数的积。这样得到许多不相等的积中,最多有多少个能被6整除?( )A. 18B.20C.21D.26
题目
有分别写着1,2,3,…,13的卡片各两张,任意抽出两张,计算这两张卡片上的数的积。这样得到许多不相等的积中,最多有多少个能被6整除?( )
A. 18
B.20
C.21
D.26
相似考题
参考答案和解析
正确答案:C
在这些能被6整除的积中,最小的为6×1.最大的为12×13 =6×26。在6×1,6×2,…,6×26这26个数中,只有6×17,6×19,6×21,6×23,6×25这5个积不能得到,从而得到的积最多有26 -5=21(个)。
[解二]由解一可知,最小积为6,最大积为6×26。则有:
(I)先取出6,再取出的数可以为1,2,3,…,13。其乘积为范围为6-78:
(2)先取出9,再取出的数必须为偶数,即2,4,6,8,10,12。其乘积范围为18-108。
(3)先取出12,再取出的数与12的乘积应大于78,则再取出的数可以为7,8,9,10,11,12,13。其乘积范围为84-156。
注意:三种情况之间的乘积有交叉情况。(1)与(2)之间重合的乘积有18,36,54,72; (2)与(3)之间重合的乘积有108。故本题的乘积能被6整除的个数为13+1+7—21。
更多“有分别写着1,2,3,…,13的卡片各两张,任意抽出两张,计算这两张卡片上的数的积。这样得到许多不相等 ”相关问题
-
第1题:
10张卡片上分别写着从1到10的自然数,小王和小张分别从中抽出两张卡,并计算其中较大数字除以较小数字的结果,小王先抽,他抽到的卡片是3和9,小张在剩下卡片中抽取,计算出的结果比小王计算的结果大的概率:A.小于20%
B.在20%到30%之间
C.在30%到40%之间
D.大于40%答案:C解析:第一步,本题考查概率问题,属于分类分步型,用枚举法解题。
第二步,小王抽到的卡片是3和9,其计算结果为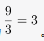
小张从剩下的1、2、4、5、6、7、8、10中任意抽取2张卡片,其结果比3大,假设小张抽取的较大数字的卡片情况如下:
抽到10,则第二张卡片可以是1、2,共2种;
抽到8,则第二张卡片可以是1、2,共2种;
抽到7,则第二张卡片可以是1、2,共2种;
抽到6、5或4,则第二张卡片都只能是1。共3种;
第三步,小张计算的结果比小王计算的结果大的情况数为2+2+2+3=9(种);总情况数为从剩下的8个数中抽取2个,有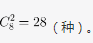
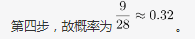
-
第2题:
6张不同卡片两张一组分别装入甲乙丙3个袋中,指定两张要在同一组,不同装法有( )种A.12
B.18
C.24
D.30
E.36答案:B解析: -
第3题:
四张卡片上分别写有数字1,2,3,4,从这4张卡片中任意抽取两张,则取出的两张卡片数字之和为奇数的概率为
A.1/3
B.1/2
C.2/3
D.3/4
C -
第4题:
20张写有数的卡片,正面的数分别是1,2,3,…,19,20,将卡片背朝上放在桌上,试问:最少取出几张,才能保证取出的卡片中一定有两张上的数相差正好是5()
A.5
B.8
C.10
D.11答案:D解析:将卡片分咸10组,每组两张,并且每组两张卡片上的数的差等于5:(1,6),(2,7),(3,8),(4,9),(5,10),(11,16),(12,17),(13,18),(14,19),(15,20)。只要其中一组卡片被取出,就达到要求。从最坏的情况来看,先取出每组前一张卡片共10张.而再任意取出一张就可以达到要求.故最少取出10+1=11张.@niutk -
第5题:
3、四张卡片上分别写有数字1,2,3,4,从这4张卡片中任意抽取两张,则取出的两张卡片数字之和为奇数的概率为
A.1/3
B.1/2
C.2/3
D.3/4
C
