已知∑={0,1}上的正规表达式0*1(0|10*1)*,它和下列哪个图的NFA等价,(27)。A.B.C.D.
题目
已知∑={0,1}上的正规表达式0*1(0|10*1)*,它和下列哪个图的NFA等价,(27)。
A.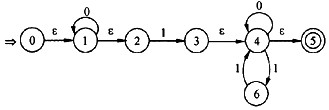
B.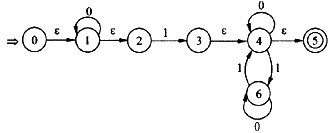
C.
D.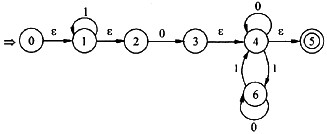
相似考题
更多“ 已知∑={0,1}上的正规表达式0*1(0|10*1)*,它和下列哪个图的NFA等价,(27)。A.B.C.D. ”相关问题
-
第1题:
某一非确定性有限自动机(NFA)的状态转换图如下图所示,与该NFA等价的正规式是(请作答此空),与该NFA等价的DFA是( )。 A.0*|(0|1)0
A.0*|(0|1)0
B.(0|10)*
C.0*((011)0)*
D.0*(10)*答案:B解析: -
第2题:
10、接受∑={0,1}上所有倒数第二个字符为1的字符串,相应的正规式为
A.(0*|1*) 10
B.(0*|1*) 1(0|1)
C.(0|1) * 11
D.(0|1)* 1(0|1)
错误 -
第3题:
1、构造下列正规式相应的DFA. 1(0|1)*101 b((ab)*|bb)*ab 2、已知NFA=({x,y,z},{0,1},M,{x},{z}),其中:M(x,0)={z},M(y,0)={x,y},,M(z,0)={x,z},M(x,1)={x},M(y,1)=φ,M(z,1)={y},构造相应的DFA。 3、将下图确定化:(sorry,图传不上来,请看书中图3.16)
无 -
第4题:
已知NFA=({x,y,z},{0,1},M,{x},{z}),其中:M(x,0)={z},M(y,0)={x,y},,M(z,0)={x,z},M(x,1)={x},M(y,1)=φ,M(z,1)={y},构造相应的DFA。
‘xyxyxywwy’ -
第5题:
对下面情况给出DFA及正规表达式: {0,1}上的含有子串010的所有串;
该语言的正规式为:(0*100*)* 首先构造该正规式的非确定有限自动机,如图3—55所示。 用子集法确定化后,得到如图3-56所示的正规式(0 * 100 * ) * 的未化简的确定有限自动机。 化简后得到如图3-57所示的正规式(0 * 100 * ) * 的化简后的确定有限自动机。
