某一非确定性有限自动机(NFA)的状态转换图如图2-6所示，与该NFA等价的正规式是(12)，与该NFA等价的DFA是(13)。A．0*｜(0｜1)0B．(0｜10)*C．0*[(0｜1)0]*D．0*(10)*
题目
某一非确定性有限自动机(NFA)的状态转换图如图2-6所示，与该NFA等价的正规式是(12)，与该NFA等价的DFA是(13)。
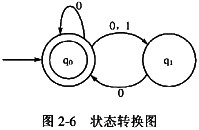
A．0*｜(0｜1)0
B．(0｜10)*
C．0*[(0｜1)0]*
D．0*(10)*
相似考题
更多“某一非确定性有限自动机(NFA)的状态转换图如图2-6所示，与该NFA等价的正规式是(12)，与该NFA等价的DFA是(13)。A．0*｜(0｜1)0B．(0｜10)*C．0*[(0｜1)0]*D．0*(10)*”相关问题
-
第1题：
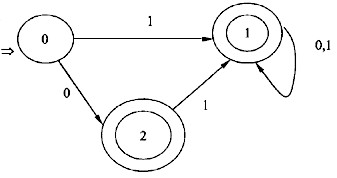
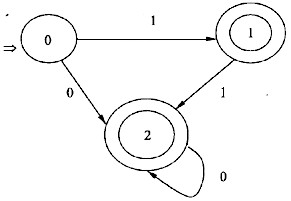
对于下图的NFA，其等价的DFA是(27)。
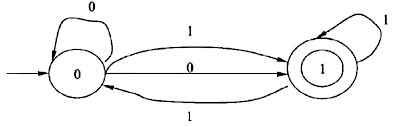
A．
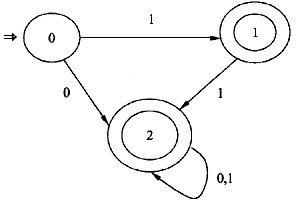
B．
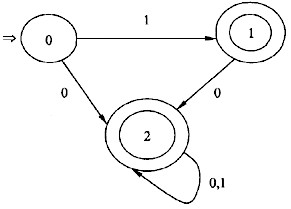
C．
D．
正确答案：A
解析：对于任何一个NFAM，都存在一个DFAM'，使得L(M')=L(M)从M出发构造M'的方法是：让M'的状态对应M的状态集合，即若δ(q，a)={q1,q2,…，qk}，则集合{q1，q2，…，qk}作为M'中的一个状态，这个方法称为子集构造法。对于图中的NFAM，没有ξ弧，其转换函数如下：δ(0,0)={0，1}δ(0,1)={1}δ(1,0)=δ6(1，1)={0,1}δ({0，1}，0)=δ(0,0)∪δ(1,0)={0，1}δ({0，1}，1)=δ(0,1)∪δ(1，1)={0,1}对上面的状态重新命名，就是被选择答案中的A。 -
第2题：
图8-2为一个DFA的状态转换图，与其等价的正规表达式是(31)，在图中状态(32)是可以合并的状态。
A．(0|1)*11(0*1*)*
B．(0|1)*110*|1*
C．(0*1*)11(0|1)*
D．(0*|1*)*11(0*|1*)
正确答案：A
-
第3题：
某一非确定性有限自动机(NFA)的状态转换图如下图所示，与该NFA等价的正规式是(28)，与该NFA等价的DFA是(29)。
A．0*|(0|1)0
B．(0|10)*
C．0*((0|1)0)*
D．0*(10)*
正确答案：B
解析：根据分析题目中给出的状态转换图可知，该NFA可识别空串以及任意数目0组成的串，但若出现1，则其后至少要有1个0才能到达终态，因此，该自动机识别的串等价于正规式(0|10)*。 -
第4题：
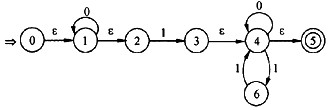
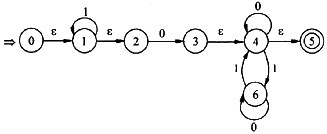
已知∑={0,1}上的正规表达式0*1(0|10*1)*，它和下列哪个图的NFA等价，(27)。
A．
B．
C．
D．
正确答案：B
解析：对于任一正规表达式R，可按如下方法构造出与之等价的非确定的有限自动机。①对于正规式R，可用下图所示的拓广状态图表示。②通过对正规式R进行分裂并加入新的结点，逐步把图转变成每条弧上的标记是∑上的一个字符或ε，转换规则如下图所示。最后所得的图即为一个NFAM，x为初态结点，y为终态结点。显然，L(M)=L(R)。按照上述方法构造正规表达式0*1(0|10*1)*的非确定的有限自动机的过程如下所示。 -
第5题：
某一确定有限自动机(DFA)的状态转换图如图2-1所示，该DFA接受的字符串集是(7)，与之等价的正规式是(8)。
A．以1开头的二进制代码串组成的集合
B．以1结尾的二进制代码串组成的集合
C．包含偶数个0的二进制代码串组成的集合
D．包含奇数个0的二进制代码串组成的集合
正确答案：C
-
第6题：
若将有限状态自动机(DFA)识别的0、1符号串看作二进制数，则(6)识别的是能被十进制数3整除的正整数，(7)是与该自动机等价的正规式。
A．
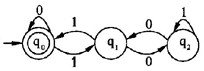
B．
C．
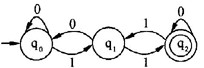
D．
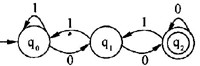正确答案：A
解析：任何一个整数被3除后，余数或为0、或为1、或为2。因此，若将该DFA识别的0、 1串看作是二进制整数，则有以下结论：
▲ 0被3除，余数为0。
▲ 设能被3整除的二进制数为x。若在x之后连接一个0所得的数为y，则y=2x，且y被3整除的余数仍然为0。若在x之后连接一个1所得的数为y，则y=2x+1，因此， y被3整除的余数将等于1。
▲ 设被3整除后余数为1的二进制数为x。若在x之后连接一个0所得的数为y，则y=2x，且y被3整除的余数为2。若在x之后连接一个1所得的数为y，则y2x+l，且y被3整除的余数将等于0。 ‘
▲ 设被3整除后余数为2的二进制数为x。若在x之后连接一个0所得的数为y，则y=2x，且y被3整除的余数为1。若在x之后连接一个1所得的数为y，则y=2x+l，且y被3整除的余数仍等于2。
综上，设被3除后的余数为0用qo(下标)表示、余数为1用q1(下标)表示、余数为2用q2(下标)表示，若将空串的值看作0，则下图所示的自动机识别的是能被3整除的整数，其正规式为(0* (1(01*0)*1)*)*。
若限定该自动机识别的0、1序列不能为空串，则相应自动机的状态转换图如下图所示。
-
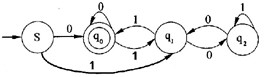
第7题：
某非确定的有限自动机（NFA）的状态转换图如下图所示（q0既是初态也是终态），与该NFA等价的确定的有限自动机（DFA）是 （ ） 。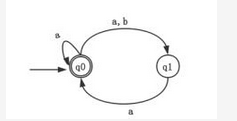
答案：A解析：本题考查有限自动机这一知识点。容易看出，能被题中不确定的有限自动机接受的符号串有两种情形，一种是???表示的符号串，另一种是(ba)?符号串。在四个选项中，只有A选项的有限自动机能同时接受???和(ba)?这两种符号串，故本题选择A选项。 -
第8题：
某一非确定性有限自动机（NFA）的状态转换图如下图所示，与该NFA等价的正规式是（ ），与该NFA等价的DFA是（请作答此空）。
答案：A解析： -
第9题：
某非确定的有限自动机（NFA）的状态转换图如下图所示（q0既是初态也是终态）。以下关于该NFA的叙述中，正确的是（ ）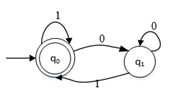
A.其可识别的0、1序列的长度为偶数
B.其可识别的0、1序列中0与1的个数相同
C.其可识别的非空0、1序列中开头和结尾字符都是0
D.其可识别的非空0、1序列中结尾字符是1答案：D解析：要证明一种说法有误只需要举一反例即可，所以做这类题时，举反例排除错误选择是一个不错的选择。
由于题目所述的NFA可以解析串“1”，所以可排除：A，B，C三个选项 -
第10题：
下图所示为一个不确定有限自动机（NFA）的状态转换图。该 NFA 识别的字符串集合可用正规式（ ）描述。
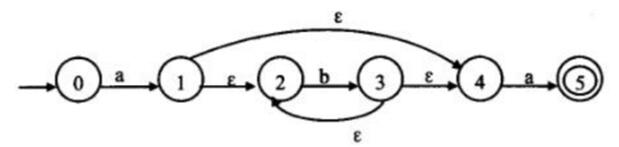A.ab*a
B.（ab）*a
C.a*ba
D.a（ba）*答案：A解析：将四个选项分别带入可以得出答案。 -
第11题：
某一确定有限自动机(DFA.的状态转换图如下图所示，该DFA接受的字符串集是 ( ) ，与之等价的正规式是 (请作答此空) 。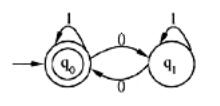
A.1*0(0|1)*
B.((0|1*0)*1*)*
C.1*((0|1)0)*
D.(1*(01*0)*)*答案：D解析：分析题日中给出的状态转换图可知，状态q0为唯一的终态，因此该DFA可识别空串。以一个。离开状态q0然后再以一个0返回q0，因此，该自动机识别的串是包含偶数个0的二进制代码串。正规式中的运算符“|”、“•”、“*”分别称为“或”、“连接”和“闭包”。在正规式的书写中，连接运算符“•”可省。运算的优先级从高到低顺序排列为：“*”、“•”、“|”。正规式1*0(0|1)*、((0|1*0)*1*)*、1*((0|1)0)*都没布表示出偶数个零的特点，因此包含偶数个0的二进制代码串的正规式为(1*(01*0)*)*。 -
第12题：
下图所示为一个不确定有限自动机（NFA）的状态转换图，与该NFA等价的 DFA是（ ）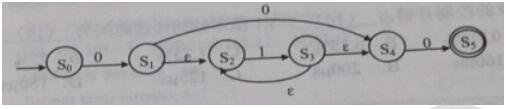
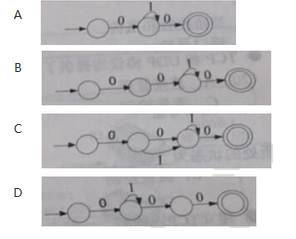答案：C解析：NFA可以有000状态，因此排除A；NFA可以有010状态，可以排除BD。 -
第13题：
某一确定性有限自动机(DFA)的状态转换图如图6-5所示，令d=0|1|2|…|9，则以下字符串中，不能被该DFA接受的是(3)，与该DFA等价的正规式是(4)。 (其中，ε表示空字符)
①3857
②1.2E+5
③-123
④.576E10
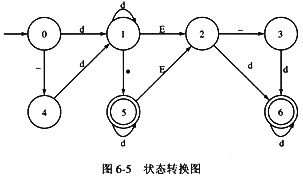
A．①、②、③
B．①、②、④
C．②、③、④
D．①、②、③、④
正确答案：B
-
第14题：
某一非确定性有限自动机(NFA)的状态转换图如图6-1所示，该NFA等价的正规式是(1)，与该NFA等价的DFA是(2)。
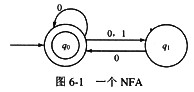
A．0*|(0|1)0
B．(0|10)*
C．0*((0|1)0)*
D．0*(10)*
正确答案：B
-
第15题：
● 某确定性有限自动机（DFA）的状态转换图如下图所示，令 d=0|1|2|...|9，则以下字符串中，能被该DFA 接受的是 （49） 。
（49）
A. 3857
B. 1.2E+5
C. -123.67
D. 0.576E10
正确答案：C
-
第16题：
某确定性有限自动机(DFA)的状态转换图如下图所示，令d=0|1|2|…|9，则以下字符串中，能被该DFA接受的是(22)。
A．3857
B．1.2E+5
C．-123.67
D．0.576E10
正确答案：C
解析：本题程序语言翻译基础知识。翻译高级语言源程序的第一步工作是进行词法分析，即将源程序中的单词(记号)识别出来，该过程可用有限自动机描述。自动机M识别一个字符串的过程是从开始状态出发，根据字符串中的字符依次进行状态转移，若能到达终态且字符串结束，则该字符串可被自动机M识别。考查题目中的选项，3857的识别过程是状态0→状态1→状态1→状态1，状态1不是终态；字符串1.2E+5中的“+”不能识别；字符串0.576E10的识别过程是状态0→状态1→状态5→状态6→状态6，在状态6下不能识别E。字符串-123.67的识别过程是状态0→状态4→状态1→状态1→状态5→状态6→状态6，因此该字符串可被厦中的自动机识别。 -
第17题：
某一确定性有限自动机(DFA)的状态转换图如图2-2所示，令d=0｜1｜2｜…19，则以下字符串中，不能被该DFA接受的是(9)，与该DFA等价的正规式是(10)。(其中，ε表示空字符。)
A．①②③
B．①②④
C．②③④
D．①②③④
正确答案：B
-
第18题：
下图是一个非确定有限自动机（NFA）的状态转换图，其中，S0为初态，S3为终态，该NFA可识别字符串（）（即找出从初态到终态的路径上所标记的字符序列）
A.0101
B.0011
C.1100
D.1010答案：A解析：判断一个字符串能否被指定的自动机识别,就是在该自动机的状态图中能否找到从开始状态到达终止状态的路径，且路径上的字符串等于需要识别的字符串。 -
第19题：
某一非确定性有限自动机（NFA）的状态转换图如下图所示，与该NFA等价的正规式是（请作答此空），与该NFA等价的DFA是（ ）。
A.0*|（0|1）0
B.（0|10）*
C.0*（（011）0）*
D.0*（10）*答案：B解析： -
第20题：
下图所示为一个不确定有限自动机的状态转换图，与该NFA等价的DFA是（ ）。
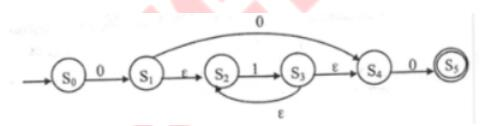
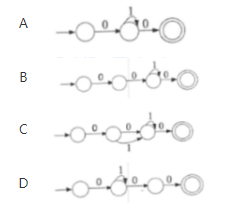答案：C解析：本题可以直接以实例方式排除错误选项。本题给出的NFA，能够识别字符串000,010等，以这两个字符串为例进行分析。与之等价的DFA，也必须能够识别这样的串。A选项不能识别000，B选项不能识别010，D选项不能识别010.只有C选项能够同时识别这2个串，因此本题选择C选项 -
第21题：
某一确定有限自动机(DFA.的状态转换图如下图所示，该DFA接受的字符串集是 (请作答此空) ，与之等价的正规式是 ( ) 。
A.以1开头的二进制代码串组成的集合
B.以1结尾的二进制代码串组成的集合
C.包含偶数个0的二进制代码串组成的集合
D.包含奇数个0的二进制代码串组成的集合答案：C解析：分析题日中给出的状态转换图可知，状态q0为唯一的终态，因此该DFA可识别空串。以一个。离开状态q0然后再以一个0返回q0，因此，该自动机识别的串是包含偶数个0的二进制代码串。正规式中的运算符“|”、“•”、“*”分别称为“或”、“连接”和“闭包”。在正规式的书写中，连接运算符“•”可省。运算的优先级从高到低顺序排列为：“*”、“•”、“|”。正规式1*0(0|1)*、((0|1*0)*1*)*、1*((0|1)0)*都没布表示出偶数个零的特点，因此包含偶数个0的二进制代码串的正规式为(1*(01*0)*)*。 -
第22题：
下图所示为一个不确定有限自动机（NFA）的状态转换图。该NFA不可识别字符串（ ）。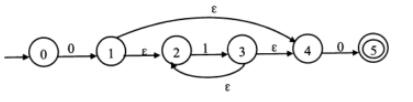
A.0110
B.01110
C.00
D.1010答案：D解析：将选项依次带入图中，注意该自动机可以识别空字符。
-
第23题：
某确定的有限自动机（DFA）的状态转换图如下图所示（0 是初态，4 是终态），则该 DFA能识别（49）。
A.aaab
B.abab
C.bbba
D.abba答案：A解析：将选项分别带入判断。