阅读以下说明和流程图，回答问题1～2，将解答填入对应的解答栏内。[说明]下面的流程图描述了计算自然数1到N(N≥1)之和的过程。[流程图][问题1] 将流程图中的(1)～(3)处补充完整。[问题2] 为使流程图能计算并输出1*3+2*4+…+N*(N+2)的值，A框内应填写(4)；为使流程图能计算并输出不大于N的全体奇数之和，B框内应填写(5)。

题目

阅读以下说明和流程图，回答问题1～2，将解答填入对应的解答栏内。

[说明]

下面的流程图描述了计算自然数1到N(N≥1)之和的过程。

[流程图]

[问题1] 将流程图中的(1)～(3)处补充完整。

[问题2] 为使流程图能计算并输出1*3+2*4+…+N*(N+2)的值，A框内应填写(4)；为使流程图能计算并输出不大于N的全体奇数之和，B框内应填写(5)。

相似考题

1.阅读以下说明和流程图，填补流程图中的空缺(1)一(5)，将解答填入答题纸的对应栏内。【说明】下面的流程图采用公式ex=1+x+x2／2 1+x3／3 1+x4／4 1+…+xn／n!+???计算ex的近似值。设x位于区间(0，1)，该流程图的算法要点是逐步累积计算每项xx／n!的值(作为T)，再逐步累加T值得到所需的结果s。当T值小于10-5时，结束计算。【流程图】

2.阅读以下说明和流程图，回答问题1-2，将解答填入对应的解答栏内。[说明]下面的流程图采用欧几里得算法，实现了计算两正整数最大公约数的功能。给定正整数m和 n，假定m大于等于n，算法的主要步骤为：(1)以n除m并令r为所得的余数；(2)若r等于0，算法结束；n即为所求；(3)将n和r分别赋给m和n，返回步骤(1)。[流程图][问题1] 将流程图中的(1)～(4)处补充完整。[问题2] 若输入的m和n分别为27和21，则A中循环体被执行的次数是(5)。

3.阅读以下说明，回答问题，将解答填入对应的解答栏内。. [说明] 请完成流程图以描述在数据A(1)至A(10)中求最大数和次大数的程序的算法。并将此改成PAD图。该算法的流程图如下图：

4.阅读以下说明和流程图，回答问题1和问题2。【说明】设8位二进制代码B0B1…B7中的最高位B0为奇偶校验位。对于任何给定的代码B1B2…B7，可按下式计算偶校验位：其中，“”表示“异或”运算。下面的流程图描述了计算偶校验位的过程。【流程图】注：流程图中，循环开始的说明按照“循环变量名：循环初值，循环终值，增量”格式描述。将流程图中的(1)～(4)处补充完整。

更多“ 阅读以下说明和流程图，回答问题1～2，将解答填入对应的解答栏内。[说明]下面的流程图描述了计算自然数1到N(N≥1)之和的过程。[流程图][问题1] 将流程图中的(1)～(3)处补充完整。[问题2] 为使流程图能”相关问题

  • 第1题：

    阅读以下说明和流程图，回答问题将解答填入对应栏。

    [说明]

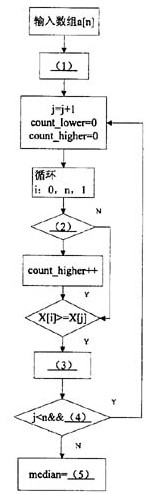
    下面的流程图，用来完成计算一组数组中的中值，其方法是：将数组中的一个值与其他值比较，并计算大于等于被比较数的数值的个数，以及小于等于被比较数的数值的个数，如果两数都大于n/2，则已经找到了中值，否则继续之前的步骤。

    注：流程中循环开始的说明按照“循环变量：循环初值，循环终值，增量”格式描述；

    [问题]

    将流程图的(1)～(5)处补充完整。


    正确答案：(1) j=-1； (2) x[j]!=x[i]； (3) count_lower++； (4) count_lower(n/2.0)||count higher(n/2.0)； (5) x[j];
    (1) j=-1； (2) x[j]!=x[i]； (3) count_lower++； (4) count_lower(n/2.0)||count higher(n/2.0)； (5) x[j]; 解析：本题目考查流程图。
    算法描述在题目中已经详细给出，通过阅读题目可知j用来定位数组中一个被比较的数，i用来循环遍历数组中所有的数。j应该从第0个数开始，又由于要执行一步j=j+1，所以(1)中应填入“j=-1”，counUligher++说明遍历的数比被比较的数大，即(2)中应填入“x[j]!=x[i]”相应的，(3)中就应填入“count_lower++”，题目说明中已经指出，当count_lower和count_higher都大于n/2时，就说明找到了中值，所以(4)应当填入“count_lower(n/2.0)][count_higher(n/2.0)”，最后，如果循环结束，则x[i]就应该是中值，(5)中应填入“x[j]”。

  • 第2题：

    阅读说明和流程图，填补流程图中的空缺（1）?（5），将答案填入答题纸对应栏内。【说明】本流程图用于计算菲波那契数列{a1=1，a2=1，…,an=an-1+an-2!n=3,4,…}的前n项（n>=2) 之和S。例如，菲波那契数列前6项之和为20。计算过程中，当前项之前的两项分别动态地保存在变量A和B中。【流程图】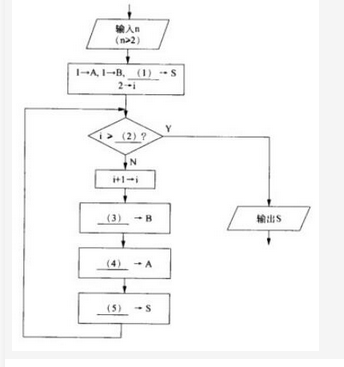


    答案：
    解析：
    （1）2或A+B（2）n（3）A+B（4）B-A（5）S+B
    【解析】

    菲波那契数列的特点是首2项都是1，从第3项开始，每一项都是前两项之和。该数列的前几项为1，1，2, 3，5，8，…。在流程图中，送初始值1—A，2—B后，显然前2项的和S应等于2,所以（1）处应填2 (或A+B)。此时2→i (i表示动态的项编号），说明已经计算出前2项之和。接着判断循环的结束条件。显然当i=n时表示已经计算出前n项之和，循环可以结束了。因此（2）处填n。判断框中用“>”或“≥”的效果是一样的，因为随着i的逐步增1，只要有i=n结束条件就不会遇到i>n的情况。不过编程的习惯使循环结束条件扩大些，以防止逻辑出错时继续循环。接下来i+1→i表示数列当前项的编号增1，继续往下计算。原来的前两项值（分别在变量A和B中）将变更成新的前两项再放到变量A和B中。

    首先可以用A+B—B实现（原A) + (原B)—(新B)，因此（3）处填A+B。为了填新A值（原来的B值)，不能用B—A，因为变量B的内容已经改变为（原A) + (原B)，而B-A正是（（原A) + (原B))-(原A)=(原B)，因此可以用B-A—A来实现新A的赋值。这样，（4）处填B-A。最后应是前n项和值的累加（比原来的S值增加了新B值)，所以（5）处应填S+B。填完各个空后，最好再用具体的数值来模拟流程图走几个循环检查所填的结果（这是防止逻辑上出错的好办法）。

  • 第3题：

    阅读以下说明和流程图，填写流程图中的空缺，将解答填入答题纸的对应栏内。【说明】设[a1b1],[a2b2],...[anbn]是数轴上从左到右排列的n个互不重叠的区间（a1


    答案：
    解析：
    1.A2.ai3.bi4.A 、B5.B
    【解析】

    若A≤ai则输出A，反之输出ai。若A≤bi不满足则输出bi，依次类推。

  • 第4题：

    阅读以下说明和流程图，回答问题，并将解答填入对应栏内。

    【说明】

    求解约瑟夫环问题。算法分析：n个士兵围成一圈，给他们依次编号，班长指定从第w个士兵开始报数，报到第s个士兵出列，依次重复下去，直至所有士兵都出列。

    【流程图】

    【问题】

    将流程图中的(1)～(5)处补充完整。


    正确答案：(1)L[i].nextp=1 (2) k=w-1 (3) count!=n (4) ++I (5) ++count
    (1)L[i].nextp=1 (2) k=w-1 (3) count!=n (4) ++I (5) ++count

  • 第5题：

    第一题 阅读以下说明和流程图，填补流程图中的空缺，将解答填入答题纸的对应栏内。
    【说明】
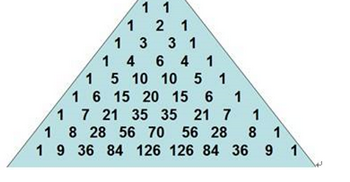
    对于大于1的正整数n，(x+1)n可展开为

    问题：1.1 【流程图】

    注：循环开始框内应给出循环控制变量的初值和终值，默认递增值为1。
    格式为：循环控制变量=初值，终值，递增值。


    答案：
    解析：
    （1）2，n，1
    （2）A[k]
    （3）k-1，1，-1
    （4）A[i]+A[i-1]
    （5）A[i]
    【解析】

    （1）（3）空为填写循环初值终值和递增值，题目中给出的格式为循环控制变量=初值，终值，递增值。按照题意，实质为求杨辉三角。如下图：

相关内容