阅读以下说明和流程图，回答问题1和问题2。【说明】设8位二进制代码B0B1…B7中的最高位B0为奇偶校验位。对于任何给定的代码B1B2…B7，可按下式计算偶校验位：其中，“”表示“异或”运算。下面的流程图描述了计算偶校验位的过程。【流程图】注：流程图中，循环开始的说明按照“循环变量名：循环初值，循环终值，增量”格式描述。将流程图中的(1)～(4)处补充完整。
题目
阅读以下说明和流程图，回答问题1和问题2。
【说明】
设8位二进制代码B0B1…B7中的最高位B0为奇偶校验位。对于任何给定的代码
B1B2…B7，可按下式计算偶校验位：
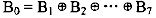
其中，“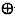
”表示“异或”运算。
下面的流程图描述了计算偶校验位的过程。
【流程图】
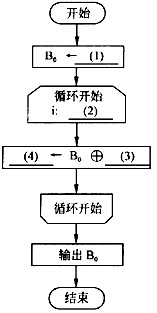
注：流程图中，循环开始的说明按照“循环变量名：循环初值，循环终值，增量”格式描述。
将流程图中的(1)～(4)处补充完整。
相似考题
更多“ 阅读以下说明和流程图，回答问题1和问题2。【说明】设8位二进制代码B0B1…B7中的最高位B0为奇偶校验位。对于任何给定的代码B1B2…B7，可按下式计算偶校验位：其中，“”表示“异或”运算。下面的流程图描述了计”相关问题
-
第1题：
阅读下列说明和流程图，将应填入(n)的语句写在对应栏内。
【流程图】
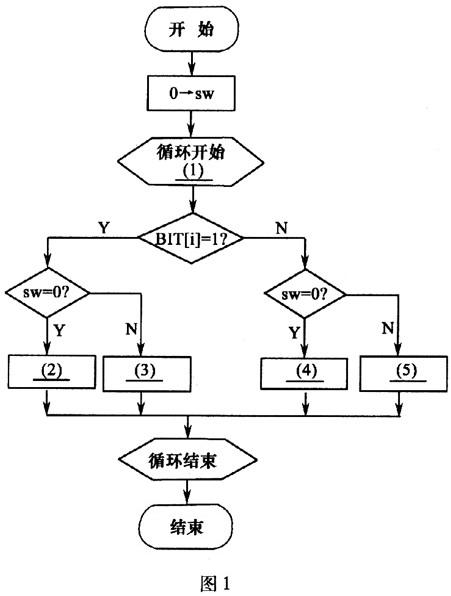
下面的流程图描述了对16位二进制整数求补的算法。计算过程是：从二进制数的低位 (最右位)开始，依次向高位逐位查看，直到首次遇到“1”时，停止查看。然后，对该“1”位左面的更高位(如果有的话)，逐位求反，所得的结果就是对原二进制数求补的结果。
例如：对二进制整数10111001 10101000求补的结果是01000110 01011000。
设16位二进制整数中的各位，从低位到高位，依次存放在整型数组BIT的BIT[1]～BIT[16]中。例如，二进制整数10111001 10101000存放在数组BIT后，就有BIT1[1]=0， BIT[2]=0，……，BIT[15]=0，BIT[16]=1。
流程图(如图1所示)中(1)处按“循环变量名：循环初值，增量，循环终值”格式描述。若流程图中存在空操作，则用NOP表示。
正确答案：(1)i: 1 1 16 (2)1-＞sw (3)0→BIT[i] (4) NOP或空操作 (5)1-＞BIT[i]
(1)i: 1, 1, 16 (2)1-＞sw (3)0→BIT[i] (4) NOP,或空操作 (5)1-＞BIT[i] 解析：该流程图的功能在说明中已经解释了，要解该题关键要搞清楚流程图中引用的变量sw的含义。通过阅读流程图的说明和流程图可知，变量sw主要用来定义是否已经找到某一位是“1”：当sw=0时，说明到目前为止还没有哪一位是“1”，不需要对该位求反；当sw=1时，说明已经有一位是“1”，需要对该位求反。
先来看(1)空。(1)空是要写出循环变量名、循环初值、增量和循环终值，该题要从遍历整型数组BIT的所有元素，从BIT[1]开始到BIT [16]结束，再看流程图的第1个判断用的变量是i，这样就可判断循环变量名为i，循环初值为1，增量为1，循环终值为16。这样(1)空的答案为“i:1,1,6”。
在这个循环中，当第i位是1时，即BIT(i)=1，进入左分支。这时需要判断sw值，若sw=0，需要将sw置为1；“若sw=1，需要对将BIT(i)置为 0。这样(2)空的答案为“1-＞sw”；(3)空的答案为“0-＞BIT[i]”。
同样，当第i位是。时，即BIT(i)=0，进入右分支。这时需要判断 sw值，若sw=0，将不作任何操作；若sw=1，需要对将BIT(i)置为1。这样(4)空的答案为“NOP”；(5)空的答案为“1-＞BIT[i]”。 -
第2题：
阅读以下说明，回答问题，将解答填入对应的解答栏内。
. [说明] 请完成流程图以描述在数据A(1)至A(10)中求最大数和次大数的程序的算法。并将此改成PAD图。该算法的流程图如下图：
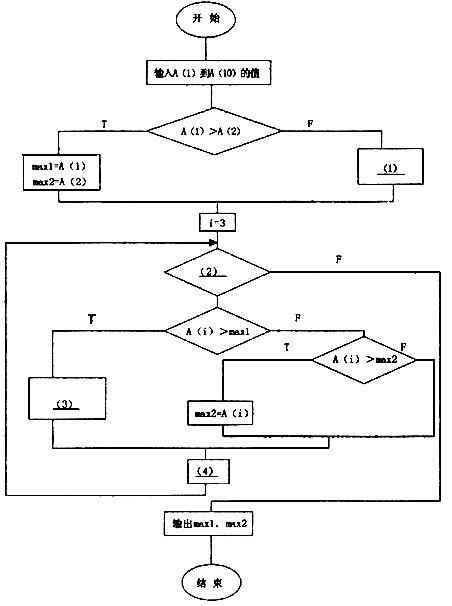正确答案：(1)max2 =A(1) mex1 =A(2) (2)i< =10 (3)max1 =A(i)1 max2 = max1 (4)i=i+1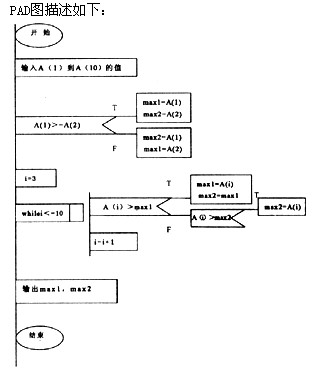
(1)max2 =A(1) mex1 =A(2) (2)i< =10 (3)max1 =A(i)1 max2 = max1 (4)i=i+1 解析：本题的算法思想是：先输入A(1)到A(10)的值，然后判断前两个数的大小。用变量max1存储最大数，用变量max2．存储次大数。然后逐个读入数据，分别和max1，max2比较，保证最大的存入max1，次大的存入max2。
-
第3题：
●试题一
阅读下列说明和流程图，将应填入(n)的语句写在答题纸的对应栏内。
【流程图】
图1
下面的流程图描述了对16位二进制整数求补的算法。计算过程是：从二进制数的低位(最右位)开始，依次向高位逐位查看，直到首次遇到"1"时，停止查看。然后，对该"1"位左面的更高位(如果有的话)，逐位求反，所得的结果就是对原二进制数求补的结果。
例如：对二进制整数10111001 10101000求补的结果是01000110 01011000。
设16位二进制整数中的各位，从低位到高位，依次存放在整型数组BIT的BIT［1］～BIT［16］中。例如，二进制整数10111001 10101000存放在数组BIT后，就有BIT1［1］=0，BIT［2］=0，……，BIT［15］=0，BIT［16］=1。
流程图(如图1所示)中 (1) 处按"循环变量名：循环初值，增量，循环终值"格式描述。若流程图中存在空操作，则用NOP表示。
正确答案：
●试题一【答案】(1)i：1，1，16(2)1->sw(3)0→BIT［i］(4)NOP，或空操作(5)1->BIT［i］【解析】该流程图的功能在说明中已经解释了，要解该题关键要搞清楚流程图中引用的变量sw的含义。通过阅读流程图的说明和流程图可知，变量sw主要用来定义是否已经找到某一位是"1"：当sw=0时，说明到目前为止还没有哪一位是"1"，不需要对该位求反；当sw=1时，说明已经有一位是"1"，需要对该位求反。先来看(1)空。(1)空是要写出循环变量名、循环初值、增量和循环终值，该题要从遍历整型数组BIT的所有元素，从BIT［1］开始到BIT［16］结束，再看流程图的第1个判断用的变量是i，这样就可判断循环变量名为i，循环初值为1，增量为1，循环终值为16。这样(1)空的答案为"i：1，1，16"。在这个循环中，当第i位是1时，即BIT(i)=1，进入左分支。这时需要判断sw值，若sw=0，需要将sw置为1；若sw=1，需要对将BIT(i)置为0。这样(2)空的答案为"1->sw"；(3)空的答案为"0->BIT［i］"。同样，当第i位是0时，即BIT(i)=0，进入右分支。这时需要判断sw值，若sw=0，将不作任何操作；若sw=1，需要对将BIT(i)置为1。这样(4)空的答案为"NOP"；(5)空的答案为"1->BIT［i］"。 -
第4题：
阅读以下说明和流程图，回答问题1-2，将解答填入对应的解答栏内。
[说明]
下面的流程图采用欧几里得算法，实现了计算两正整数最大公约数的功能。给定正整数m和 n，假定m大于等于n，算法的主要步骤为：
(1)以n除m并令r为所得的余数；
(2)若r等于0，算法结束；n即为所求；
(3)将n和r分别赋给m和n，返回步骤(1)。
[流程图]
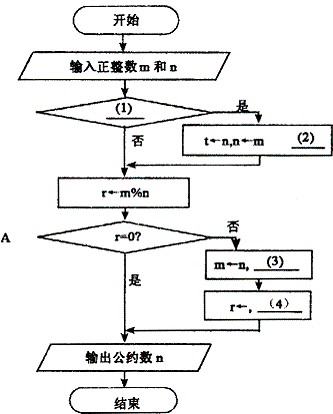
[问题1] 将流程图中的(1)～(4)处补充完整。
[问题2] 若输入的m和n分别为27和21，则A中循环体被执行的次数是(5)。
正确答案：[问题1] (1) n＞m或nm或其它等效形式 (2) m←t (3) n←r (4) m%n [问题2] (5) 1
[问题1] (1) n＞m或nm或其它等效形式 (2) m←t (3) n←r (4) m%n [问题2] (5) 1 解析：(1)～(2)当n的值大于(等于)m时，应交换两者的值，再使用欧几里得算法；
(3)～(4)略；
(5)m，n和r在执行循环A前后的值分别为：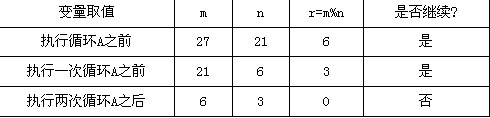
-
第5题：
阅读以下说明和流程图，回答问题将解答填入对应栏。
[说明]
下面的流程图，用来完成计算一组数组中的中值，其方法是：将数组中的一个值与其他值比较，并计算大于等于被比较数的数值的个数，以及小于等于被比较数的数值的个数，如果两数都大于n/2，则已经找到了中值，否则继续之前的步骤。
注：流程中循环开始的说明按照“循环变量：循环初值，循环终值，增量”格式描述；
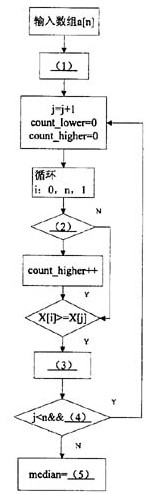
[问题]
将流程图的(1)～(5)处补充完整。
正确答案：(1) j=-1； (2) x[j]!=x[i]； (3) count_lower++； (4) count_lower(n/2.0)||count higher(n/2.0)； (5) x[j];
(1) j=-1； (2) x[j]!=x[i]； (3) count_lower++； (4) count_lower(n/2.0)||count higher(n/2.0)； (5) x[j]; 解析：本题目考查流程图。
算法描述在题目中已经详细给出，通过阅读题目可知j用来定位数组中一个被比较的数，i用来循环遍历数组中所有的数。j应该从第0个数开始，又由于要执行一步j=j+1，所以(1)中应填入“j=-1”，counUligher++说明遍历的数比被比较的数大，即(2)中应填入“x[j]!=x[i]”相应的，(3)中就应填入“count_lower++”，题目说明中已经指出，当count_lower和count_higher都大于n/2时，就说明找到了中值，所以(4)应当填入“count_lower(n/2.0)][count_higher(n/2.0)”，最后，如果循环结束，则x[i]就应该是中值，(5)中应填入“x[j]”。