阅读下列说明和流程图2-3,将应填入(n)的字句写在答题纸的对应栏内。【说明】下面的流程图描述了对8位二进制整数求补的算法。该算法的计算过程如下:从二进制数的低位(最右位)开始,依次向高位逐位查看,直到首次遇到“1”时,停止查看。然后,对该“1”位左面的更高位(如果有的话),逐位求反,所得的结果就是对原二进制数求补的结果。例如:对二进制整数10101000求补的结果是01011000。设8位二进制整数中的各位,从低位到高位,依次存放在整型数组BIT的B1T[1]~BIT[8]中。例如,二进制整数10101
题目
阅读下列说明和流程图2-3,将应填入(n)的字句写在答题纸的对应栏内。
【说明】
下面的流程图描述了对8位二进制整数求补的算法。
该算法的计算过程如下:从二进制数的低位(最右位)开始,依次向高位逐位查看,直到首次遇到“1”时,停止查看。然后,对该“1”位左面的更高位(如果有的话),逐位求反,所得的结果就是对原二进制数求补的结果。
例如:对二进制整数10101000求补的结果是01011000。
设8位二进制整数中的各位,从低位到高位,依次存放在整型数组BIT的B1T[1]~BIT[8]中。例如,二进制整数10101000存放在数组BIT后,就有BIT[1]=0,BIT[2]=0,…,BIT[7] =0,BIT[8]=1。若流程图中存在空操作,则用NOP表示。
【流程图】
注:流程图中(1)处按“循环变量名:循环初值,增量,循环终值”格式描述。
相似考题
参考答案和解析
(1)i:1,1,8 (2)1→sw (3)0→BIT[i] (4)NOP,或空操作 (5)1→BIT[i] 解析:根据题意,从二进制数的低位(最右位)开始,依次向高位逐位查看,直到首次遇到“1”时,停止查看。然后,对该“1”位左面的更高位(如果有的话),逐位求反,所得的结果就是对原二进制数求补的结果。所以(1)空是8次循环根据BIT[i]的值判断相应补数的值, (2)~(5)空是分支处理的结果。
更多“阅读下列说明和流程图2-3,将应填入(n)的字句写在答题纸的对应栏内。 【说明】 下面的流程图描述了对 ”相关问题
-
第1题:
阅读以下说明和流程图,将应填入(n)处的字句写在对应栏内。
[说明]
下面的流程图用于计算一个英文句子中最长单词的长度(即单词中字母个数)MAX。假设该英文句子中只含字母、空格和句点“.”,其中句点表示结尾,空格之间连续的字母串称为单词。
[流程图]
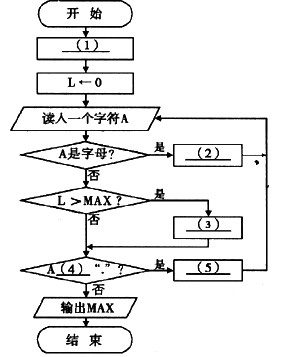 正确答案:(1)MAX←0 (2)←L+1 (3)MAX←L (4)≠ (5)L←0
正确答案:(1)MAX←0 (2)←L+1 (3)MAX←L (4)≠ (5)L←0
(1)MAX←0 (2)←L+1 (3)MAX←L (4)≠ (5)L←0 解析:本题用到的三个变量及其作用分别为:A,存放输入的一个字符;MAX,存放当前为止最长单词的长度;L,存放当前单同的长度。
(1)使用变量MAX应先赋予初值,由上下文知其初值为0;
(2)读取当前单词时,每读人一个字母,单词长度值L应增1;
(3)当前单词长度L比MAX时,应更新MAX的值;
(4)若当前字符不是句点,应当继续读取字符;
(5)读取下一个单词前,应当重置L的值。 -
第2题:
●试题一
阅读下列说明和流程图,将应填入(n)处的语句写在答题纸的对应栏内。
【说明】
下列流程图用于从数组K中找出一切满足:K(I)+K(J)=M的元素对(K(I),K(J))(1≤I≤J≤N)。假定数组K中的N个不同的整数已按从小到大的顺序排列,M是给定的常数。
【流程图】
此流程图1中,比较"K(I)+K(J)∶M"最少执行次数约为 (5) 。

图1
正确答案:
●试题一【答案】(1)(2)<(3)I+l->I(4)J-1->J(5)「N/2」【解析】该算法的思路是:设置了两个变量I和J,初始时分别指向数组K的第一个元素和最后一个元素。如果这两个元素之和等于M时,输出结果,并这两个指针都向中间移动;如果小于M,则将指针I向中间移动(因为数组K已按从小到大的顺序排列);如果大于M,则将指针J向中间移动(因为数组K已按从小到大的顺序排列)。当IJ时,说明所有的元素都搜索完毕,退出循环。根据上面的分析,(1)、(2)空要求填写循环结束条件,显然,(1)空处应填写"",(2)空处应填写"<"。这里主要要注意I=J的情况,当I=J时,说明指两个指针指向同一元素,应当退出循环。(3)空在流程图有两处,一处是当K(I)+K(J)=M时,另一处是当K(I)+K(J)<M时,根据上面分析这两种情况都要将指针I向中间移动,即"I+1->I"。同样的道理,(4)空处应填写"J-1->J"。比较"K(I)+K(J):M"最少执行次数发生在第1元素与第N个元素之和等于M、第2元素与第N-1个元素之和等于M、……,这样每次比较,两种指针都向中间移动,因此最小执行次数约为"N-2"。 -
第3题:
阅读以下说明和流程图,填写流程图中的空缺,将解答填入答题纸的对应栏内。【说明】设[a1b1],[a2b2],...[anbn]是数轴上从左到右排列的n个互不重叠的区间(a1 答案:解析:1.A2.ai3.bi4.A 、B5.B
答案:解析:1.A2.ai3.bi4.A 、B5.B
【解析】
若A≤ai则输出A,反之输出ai。若A≤bi不满足则输出bi,依次类推。 -
第4题:
●试题一
阅读下列说明和流程图,将应填入(n)的字句写在答题纸的对应栏内。
【说明】
下列流程图(如图4所示)用泰勒(Taylor)展开式
sinx=x-x3/3!+x5/5!-x7/7!+…+(-1)n×x 2n+1/(2n+1)!+…
【流程图】
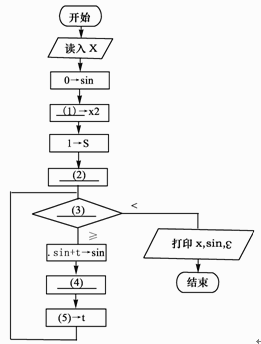
图4
计算并打印sinx的近似值。其中用ε(>0)表示误差要求。
正确答案:
●试题一【答案】(1)x*x(2)x->t(3)|t|∶ε(4)s+2->s(5)(-1)*t*x2/(s*(s-1))【解析】该题的关键是搞清楚几个变量的含义。很显然变量t是用来保存多项式各项的值,变量s和变量x2的作用是什么呢?从流程图的功能上看,需要计算1!、3!、5!,……,又从变量s的初值置为1可知,变量s主要用来计算这此数的阶乘的,但没有其他变量用于整数自增,这样就以判断s用来存储奇数的,即s值依次为1、3、5,……。但x2的功能还不明确,现在可以不用管它。(2)空的作用是给t赋初值,即给它多项式的第一项,因此应填写"x->t"。(3)空处需填写循环条件,显然当t的绝对值小于ε(>0)就表示已经达到误差要求,因此(3)空应填入"|t|∶ε"。由变量s的功能可知,(4)空应当实现变量s的增加,因此(4)空应填入"s+2->s"。(5)空应当是求多项式下一项的值,根据多项式连续两项的关系可知,当前一项为t时,后一项的值为(-1)*t*x*x/(s*(s-1))。但这样的话,每次循环都需要计算一次x*x,计算效率受到影响,联想到变量x2还没用,这时就可以判断x2就是用来存储x*x的值,使得每次循环者少进行一次乘法运算。因此(1)空处应填入"x*x",(5)空处应填入"(-1)*t*x2/(s*(s-1))"。 -
第5题:
试题三(共 15 分)
阅读以下说明和 C 程序,将应填入 (n) 处的字句写在答题纸的对应栏内。
 正确答案:
正确答案:
-
第6题:
阅读下列说明和?C++代码,将应填入(n)处的字句写在答题纸的对应栏内。
【说明】
阅读下列说明和?Java代码,将应填入?(n)?处的字句写在答题纸的对应栏内。
【说明】
某快餐厅主要制作并出售儿童套餐,一般包括主餐(各类比萨)、饮料和玩具,其餐品种
类可能不同,但其制作过程相同。前台服务员?(Waiter)?调度厨师制作套餐。现采用生成器?(Builder)?模式实现制作过程,得到如图?6-1?所示的类图。
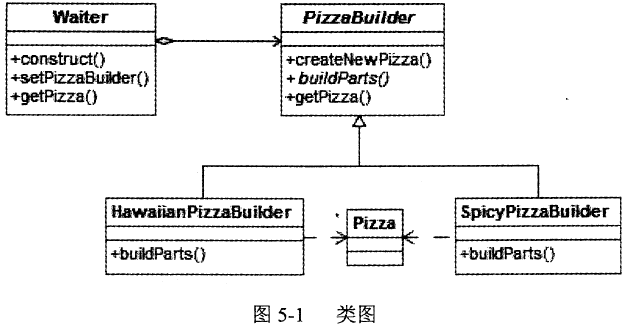


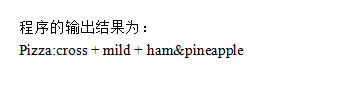 答案:解析:
答案:解析:
