商品的价格弹性在需求函数为Q=Ap－a时为一个常数。()此题为判断题(对，错)。
题目
商品的价格弹性在需求函数为Q=Ap－a时为一个常数。()
此题为判断题(对，错)。
相似考题
更多“商品的价格弹性在需求函数为Q=Ap－a时为一个常数。() ”相关问题
-
第1题：
设某种商品的需求函数是Q=a-bP,其中Q是该产品的销售量，P是该产品的价格，常数a>0,b>0，且该产品的总成本函数为
已知当边际收益MR=56以及需求价格弹性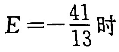
，出售该产品可获得最大利润，试确定常数a和b的值，并求利润最大时的产量。答案：解析：
-
第2题：
假设商品需求函数为Q=M/2P，其中P为价格，M为收入，收入点弹性为
D -
第3题：
假定需求函数为Q＝MP－N，其中M表示收入，P表示商品价格，N（N＞0)为常数。 求：需求的价格点弹性和需求的收入点弹性。
由Q=M/P^n,得 Em=dQ/dM*M/Q=1/P^n*M/M/P^n=1 Ep=-dQ/dP*P/Q=M*(-n)*1/P^(n+1)*P/M/P^n=-n -
第4题：
假定需求函数为Q=MP^-N其中M表示收入，P表示商品价格N（N>O）为常数 求：需求的价格点弹性和需求的收入点弹性。答案：解析：已知Q=MP^-N，可得：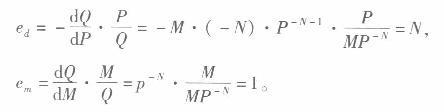
由此可见，一般地，对于幂指数需求函数Q( P) =MP^-S而言，其需求的价格点弹性总等于幂指数的绝对值N，而对于线性需求函数Q(M)=MP^-N而言，其需求的收入点弹性总是等于1。 -
第5题：
已知某商品的需求函数为Q=15-5p，求（1）p=1时的需求价格弹性；（2）如何定价能使商品属于单位弹性商品。
（1）根据均衡价格和均衡数量的定义，当商品的供求数量相等时有：Qd =Qs 。根据题中已知的供求函数，有：－10+5P=50－5P，求解得到: P=6。将P=6带入需求函数或供给函数中得到：Q=20。（2）在新的需求函数确定以后，在新的条件下供求将实现新的均衡。根据均衡的定义有:－10+5P=60－5P，求解得到：P '=7。将P '=7代入已知需求函数或供给函数得：Q '=25。（3）在需求函数不变的情况下，新的供给函数与原需求函数将决定新的均衡状态。根据均衡的定义，得到－5+5P=50－5P，求解得到：P ''=5.5。将P ''=5.5代入已知需求函数或供给函数得到：Q ''=22.5。