设有方程f(x)一0在区间[a，b]上有实根，且f(a)与f(b)异号，利用二分化法求该方程在区间[a’b]上的一个实根，采用的算法设计技术为

题目

设有方程f(x)一0在区间[a，b]上有实根，且f(a)与f(b)异号，利用二分化法求该方程在区间[a’b]上的一个实根，采用的算法设计技术为

相似考题

1.在用二分法求解方程在一个闭区间上的实根时，采用的算法没计技术是（ ）A．列举法B．归纳法C．递归法D．减半递推法

2.方程x-lnx-2=0在区间（0，+∞）内（ ）。A.没有实根 B.只有一个实根 C.有两个相异的实根 D.有两个以上相异实根

3.若a，6是方程f(x)=0的两个相异的实根，f(x)在[a，b]上连续，且在(a，b)内可导，则方程f´(x)=0在(a，b)内( ).A.只有一个根 B.至少有一个根 C.没有根 D.以上结论都不对

4.设有方程f(x)=0在区间[a，b]上有实根，且f(a)与f(b)异号，利用二分法求该方程在区间[a，b]上的一个实根，采用的算法设计技术为（ ）

更多“ 设有方程f(x)一0在区间[a，b]上有实根，且f(a)与f(b)异号，利用二分化法求该方程在区间[a’b]上的一个实根，采用的算法设计技术为 ”相关问题

  • 第1题：

    设函数f(x)在区间［0，1］上具有2阶导数，且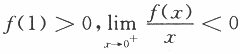，证明：
    　　(Ⅰ)方程f(x)=0在区间(0，1)内至少存在一个实根；
    　　(Ⅱ)方程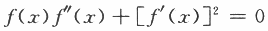在区间(0，1)内至少存在两个不同实根.


    答案：
    解析：

  • 第2题：

    1、若f（x)在[a,b]上可导，f（a)=f（b)，那么方程f'（x)=0在（a,b)内至少有一个实根。


    (1)y'=[f(e x )]'e f(x) +[e f(x) ]'f(e x ) =f'(e x )·e x ·e f(x) +e f(x) ·f'(x)·f(e x )。 =e f(x) [e x ·f'(e x )+f'(x)·f(e x )]。 (2)y'=f'(f(f(x))·f'(f(x))·f'(x)。 (1)y'=[f(ex)]'ef(x)+[ef(x)]'f(ex)=f'(ex)·ex·ef(x)+ef(x)·f'(x)·f(ex)。=ef(x)[ex·f'(ex)+f'(x)·f(ex)]。(2)y'=f'(f(f(x))·f'(f(x))·f'(x)。

  • 第3题：

    2、若f（x)在[a,b]上可导，f（a)=f（b)，那么方程f'（x)=0在（a,b)内至少有一个实根。


    正确

  • 第4题：

    方程x-lnx-2=0在区间（0，+∞）内（ ）。《》（ ）

    A.没有实根
    B.只有一个实根
    C.有两个相异的实根
    D.有两个以上相异实根

    答案：C
    解析：

  • 第5题：

    3、在区间（0,+∞)上关于函数y=f（x)=1/x 的如下哪些论述错误:

    A．f’(x)<0

    B．f(x)单调下降

    C．f’(x) 单调下降

    D．f(x)=0 有唯一实根


    ∵函数 y=x+ 1 x 在（0，1]上是减函数，在[1，+∞）上是增函数； 函数 y=x+ 2 x 在 (0， 2 ] 上是减函数，在 [ 2 ，+∞) 上是增函数； 函数 y=x+ 3 x 在 (0， 3 ] 上是减函数，在 [ 3 ，+∞) 上是增函数； ∴函数y=x+ p x （p为正常数）在（0， p ]上是减函数，在[ p ，+∞）上是增函数； ∵函数 y=x+ 3 m x (x＞0) 的值域是[6，+∞）， ∴函数在x= 3 m 取得最小值为6， ∴ 3 m + 3 m 3 m =6， 解得m=2，故答案为2．

相关内容