偶尔考考微积分,如中值定理,求复杂函数的二次导数

题目

偶尔考考微积分,如中值定理,求复杂函数的二次导数

相似考题

1.设函数f（x）=x3-3x2-9x．求（I）函数f（x）的导数；（1I）函数f（x）在区间[1，4]的最大值与最小值．

2.数学分析中的积分中值定理能推移到复变函数积分上来。()

3.微积分的基本定理是:( )。A、牛顿-莱布尼茨公式B、罗尔定理C、拉格朗日中值定理D、积分中值定理

4.根据罗尔(Rolle)定理，可以推出中值定理。()

更多“偶尔考考微积分,如中值定理,求复杂函数的二次导数”相关问题

  • 第1题：

    求下列函数的偏导数：


    答案：
    解析：

  • 第2题：

    设a，b为实数，函数z=2+ax^2+by^2在点(3，4)处的方向导数中，沿方向l=-3i-4j的方向导数最大，最大值为10.
    　　(Ⅰ)求a，b；
    　　(Ⅱ)求曲面z=2+ax^2+by^2(z≥0)的面积.


    答案：
    解析：

  • 第3题：

    求方程 所确定的隐函数的导数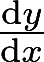


    答案：
    解析：

  • 第4题：

    叙述并证明拉格朗日微分中值定理,并简述拉格朗日中值定理与中学数学内容的联系。


    答案：
    解析：

  • 第5题：

    求函数．f(x)＝x2?2x在x=0处的n阶导数,f(n)(O)。


    答案：
    解析：
    函数乘积求高阶导数，莱布尼茨公式。

  • 第6题：

    中值选民定理


    正确答案:一个数学结论，表明如果要选民沿着一条线选一个点，而且，每个选民都想选离他最偏好的点最近的点，那么，多数原则将选出中值选民最偏好的点。

  • 第7题：

    以下关于导数叙述不对的是（）。

    • A、导数是差商的极限
    • B、导数是经济函数的边际
    • C、导数是函数的微分
    • D、导数是函数的微分与自变量的微分之商

    正确答案:C

  • 第8题：

    拉格朗日在《解析函数论》一书中，主张用（）来定义导数，以此作为整个微分、积分演算的出发点而将微积分归结为“代数运算”。


    正确答案:拉格朗日定理

  • 第9题：

    下列是对称的数学公式的是（）。

    • A、欧拉函数
    • B、薛定谔方程式
    • C、拉格朗日中值定理
    • D、海伦公式

    正确答案:D

  • 第10题：

    单选题
    精确重心法是一种以（）为基础的模型。
    A

    导数

    B

    函数

    C

    几何

    D

    微积分


    正确答案： C
    解析： 暂无解析

  • 第11题：

    单选题
    下列是对称的数学公式的是（）。
    A

    欧拉函数

    B

    薛定谔方程式

    C

    拉格朗日中值定理

    D

    海伦公式


    正确答案： C
    解析： 暂无解析

  • 第12题：

    单选题
    以下关于导数叙述不对的是（）。
    A

    导数是差商的极限

    B

    导数是经济函数的边际

    C

    导数是函数的微分

    D

    导数是函数的微分与自变量的微分之商


    正确答案： D
    解析： 暂无解析

  • 第13题：

    设函数z=f(xy，yg(x))，其中函数f具有二阶连续偏导数，函数g(x)可导且在x=1处取得极值g(1)=1.求


    答案：
    解析：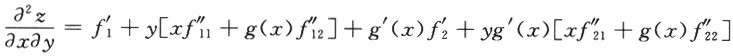

    所以，令x=y=1，且注意到g(1)=1，g'(1)=0，得

  • 第14题：

    设有三元方程 ，根据隐函数存在定理，存在点(0,1,1)的一个邻域，在此邻域内该方程

    A.只能确定一个具有连续偏导数的隐函数z=z(x,y)
    B.可确定两个具有连续偏导数的隐函数x=x(y,z)和z=z(x,y)
    C.可确定两个具有连续偏导数的隐函数y=y(x,z)和z=z(x,y)
    D.可确定两个具有连续偏导数的隐函数x=x(y,z)和y=y(x,z)

    答案：D
    解析：

  • 第15题：

    试分别叙述罗尔中值定理和拉格朗日中值定理。若以S(x)记由(a,(a))，(b，(b))，(x,(x)))三点组成的三角形面积，试对S(x)应用罗尔中值定理证明拉格朗日中值定理。


    答案：
    解析：
    罗尔中值定理：若函数(x)满足如下条件： (1)(x)在闭区间[a，b]上连续；
    (2)(x)在开区间(a，b)内可导；
    (3)(a)=(b)，
    则在(a，b)内至少存在一点ξ，使得’(ξ)=0。
    拉格朗日中值定理：若函数(x)满足如下条件：
    (1)(x)在闭区间[a，b]上连续；
    (2)(x)在开区间(a，b)内可导，

    在xOy面上考虑，记由A(a，(a)，0)，B(b，(b)，0)，C(x，(x)，0)三点组成的三角形面积S(x)，则

  • 第16题：

    叙述并证明拉格朗日微分中值定理，并简述拉格朗日微分中值定理与中学数学内容的联系。


    答案：
    解析：
    本题主要考查微分中值定理中十分重要的拉格朗日中值定理。

    证明拉格朗日微分中值定理，首先要从罗尔定理出发，

  • 第17题：

    函数y=x2-x+1在区间[-1，3]上满足拉格朗日中值定理的ξ=（　　）


    答案：D
    解析：
    y=x2-x+1在[-1，3]上满足拉格朗日中值定理，

  • 第18题：

    精确重心法是一种以（）为基础的模型。

    • A、导数
    • B、函数
    • C、几何
    • D、微积分

    正确答案:D

  • 第19题：

    可微函数的反函数一定可微，其导数与其反函数的导数互为倒数。


    正确答案:正确

  • 第20题：

    边际消费倾向递减的规律用数学语言表达是什么？（）

    • A、消费函数的一阶导数大于0，二阶导数小于0
    • B、消费函数的一阶导数大于0，二阶导数小于1
    • C、消费函数的一阶导数小于0，二阶导数小于1
    • D、消费函数的一阶导数小于0，二阶导数大于0

    正确答案:A

  • 第21题：

    单选题
    木匠计算“复杂形状地图”的面积时，采用的方法是：（）。
    A

    微积分定理

    B

    面积计算公式

    C

    称重对比法

    D

    概率统计


    正确答案： B
    解析： 暂无解析

  • 第22题：

    填空题
    拉格朗日在《解析函数论》一书中，主张用（）来定义导数，以此作为整个微分、积分演算的出发点而将微积分归结为“代数运算”。

    正确答案： 拉格朗日定理
    解析： 暂无解析

  • 第23题：

    单选题
    设三元函数xy－zlny＋exz＝1，根据隐函数存在定理，存在点（0，1，1）的一个邻域，在此邻域内该方程（　　）。
    A

    只能确定一个具有连续偏导数的隐函数z＝z（x，y）

    B

    可确定两个具有连续偏导数的隐函数y＝y（x，z）和z＝z（x，y）

    C

    可确定两个具有连续偏导数的隐函数x＝x（y，z）和z＝z（x，y）

    D

    可确定两个具有连续偏导数的隐函数x＝x（y，z）和y＝y（x，z）


    正确答案： C
    解析：
    构造函数F（x，y，z）＝xy－zlny＋exz－1，则Fx′＝y＋zexz，Fy′＝x－（z/y），Fz′＝－lny＋xexz。Fx′（0，1，1）＝2≠0，Fy′（0，1，1）＝－1≠0，Fz′（0，1，1）＝0。
    故根据隐函数的存在定理可知，方程xy－zlny＋exz＝1能确定x是y、z的具有连续偏导数的函数x＝x（y，z）；y是x、z的具有连续偏导数的函数y＝y（x，z）。因为Fz′（0，1，1）＝0不能满足定理成立的条件，故不能确定z是x、y的具有连续偏导数的隐函数z＝z（x，y）。

相关内容