设函数f（x）=x3-3x2-9x．求（I）函数f（x）的导数；（1I）函数f（x）在区间[1，4]的最大值与最小值．

题目

设函数f（x）=x3-3x2-9x．求

（I）函数f（x）的导数；

（1I）函数f（x）在区间[1，4]的最大值与最小值．

相似考题

1.设f(x)=xe-x，求函数f(x)的极值（6分）

2.若F(x)与G(x)均为f (x)在区间I上的原函数，则F(x)与G(x)相差一个_________.

3.求函数f(x)=x3-6x2+9x-4在闭区间[0，2]上的最大值和最小值.

4.设函数f(x）=e5x，则f(x)的n阶导数f(n)(x)=____．

参考答案和解析

正确答案：

更多“设函数f（x）=x3-3x2-9x．求（I）函数f（x）的导数；（1I）函数f（x）在区间[1，4]的最大值与最小值．”相关问题

第1题：

已知函数f（x）=x3-4x2．
（I）确定函数f（x）在哪个区问是增函数，在哪个区间是减函数；
（Ⅱ）求函数f（x）在区间[0，4]上的最大值和最小值．

正确答案：
第2题：

设f(x)为连续函数，F(x)是f(x)的原函数，则（）。
(A) 当f(x)是奇函数时，F(x)必为偶函数
(B) 当f(x)是偶函数时，F(x)必为奇函数
(C) 当f(x)是周期函数时，F(x)必为周期函数
(D) 当f(x)是单增函数时，F(x)必为单增函数
(E) 当f(x)是单减函数时，F(x)必为单减函数

正确答案：A
第3题：

设连续型随机变量X的分布函数为F(x)=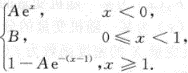
　　(1)求常数A,B;(2)求X的密度函数f(x)；(3)求P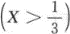

答案：
解析：
第4题：

设函数z=f(xy，yg(x))，其中函数f具有二阶连续偏导数，函数g(x)可导且在x=1处取得极值g(1)=1.求

答案：
解析：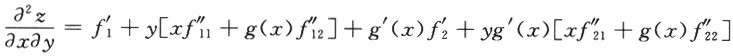

所以，令x=y=1，且注意到g(1)=1，g'(1)=0，得
第5题：

（本小题13分）已知函数f(x)=2x3-3x2，求
（1）函数的单调区间；
（2）函数f(x)在区间[-3,2]的最大值与最小值。

答案：
解析：
第6题：

设函数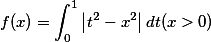,求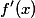并求f(x)的最小值.

答案：
解析：
第7题：

设f(x)是R上的函数，则下列叙述正确的是( )。

A、f(x)f(-x)是奇函数
B、f(x)|f(x)|是奇函数
C、f(x)-f(-x)是偶函数
D、f(x)+f(-x)是偶函数

答案：D
解析：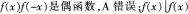
的奇偶性取决于厂(x)的奇偶性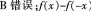是奇函数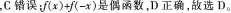
第8题：

求函数．f(x)＝x2?2x在x=0处的n阶导数,f(n)(O)。

答案：
解析：
函数乘积求高阶导数，莱布尼茨公式。
第9题：

已知函数f(x)=x2+4lnx．
(1)求函数f(x)在[1，e]上的最大值和最小值；
(2)证明：当x∈[1，+∞)时，函数八戈)的图象在g(x)=2x3的图象的下方。

答案：
解析：
第10题：

填空题
设函数y＝f（x）具有二阶导数，且f′（x）＝f（π/2－x），则该函数满足的微分方程为____。

正确答案： f″(x)+f(x)=0
解析：
由f′（x）＝f（π/2－x），两边求导得f″（x）＝－f′（π/2－x）＝－f[π/2－（π/2－x）]＝－f（x），即f″（x）＋f（x）＝0。
第11题：

填空题
设f（x）＝xex，则函数f（n）（x）在x＝____处取最小值____。

正确答案： -(n+1),-e^-(ⁿ⁺¹⁾
解析：
由f（x）＝xe^x得f^（ⁿ^）（x）＝（n＋x）e^x。令f^（ⁿ^＋¹^）（x）＝（n＋1＋x）e^x＝0，得x₀＝－（n＋1）。当x₀＞－（n＋1）时，f^（ⁿ^＋¹^）（x）＞0；当x₀＜－（n＋1）时，f^（ⁿ^＋¹^）（x）＜0。故f^（ⁿ^）（x）在x₀＝－（n＋1）处取到极小值，此时，f^（ⁿ^）（x₀）＝－e^－（ⁿ^＋¹^）。
第12题：

单选题
设函数y＝f（x）具有二阶导数，且f′（x）＝f（π/2－x），则该函数满足的微分方程为（　　）。
A
f′（x）＋f（x）＝0
B
f′（x）－f（x）＝0
C
f″（x）＋f（x）＝0
D
f″（x）－f（x）＝0

正确答案： D
解析：
由f′（x）＝f（π/2－x），两边求导得f″（x）＝－f′（π/2－x）＝－f[π/2－（π/2－x）]＝－f（x），即f″（x）＋f（x）＝0。
第13题：

设函数f（x）=x4-4x+5．
（I）求f（x）的单调区间，并说明它在各区间的单调性；
（Ⅱ）求f（x）在区间[0，2]的最大值与最小值．

正确答案：
第14题：

已知函数f(x)=（1/2）e2x-ax，g(x)=6xlnx，，h(x)=2e2x-4/x，a>o，b≠0。
(1)求函数f(x)的最小值；(3分)
(2)求函数g(x)的单调区间；(3分)
(3)证明：函数h(x)在[1/2，1]上有且仅有l个零点。(4分)

答案：
解析：
第15题：

设随机变量X的密度函数为f(x)=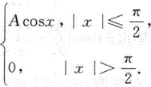
　　(1)求常数A；(2)求X在内的概率；(3)求X的分布函数F(x).

答案：
解析：
第16题：

设函数f(x)在定义域I上的导数大于零，若对任意的x0∈I，曲线y=f(x)在点(x0，f(x0))处的切线与直线x=x0及x轴所围成区域的面积恒为4，且f(0)=2，求f(x)的表达式.

答案：
解析：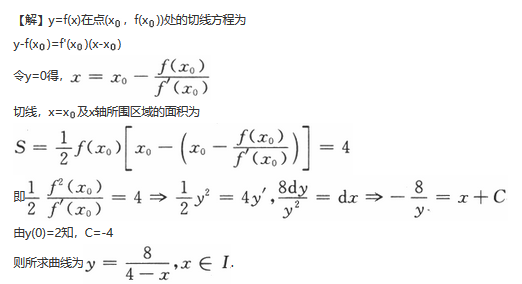
第17题：

设函数，已知函数f（x）在x=0处可微，求

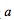答案：
解析：
第18题：

设F（x）是连续函数f（x）的一个原函数，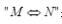

表示“M的充分必要条件是N”，则必有（　　）。

A．F（x）是偶函数f（x）是奇函数
B．F（x）是奇函数f（x）是偶函数
C．F（x）是周期函数f（x）是周期函数
D．F（x）是单调函数f（x）是单调函数

答案：A
解析：
第19题：

设函数f(x)=x1nx
(1)画出函数f(x)的草图。(6分)
(2)若
的最大值(提示利用函数f(x)的凸性)。(4分)

答案：
解析：
(1)
(2)根据f(x)的凸性有 {图2}
第20题：

设f(x)是连续函数，F(x)是f(x)的原函数，则（）。
A.当f(x)是奇函数时，F(x)必是偶函数
B.当f(x)是偶函数时，F(x)必是奇函数
C.当f(x)是周期函数时，F(x)必是周期函数
D.当f(x)是单调增函数时，F(x)必是单调增函数

答案：B
解析：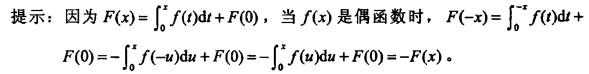
第21题：

设偶函数f（x）在区间（-1，1）内具有二阶导数，且f″（0）=f′（0）+1，则f（0）为f（x）的一个极小值。

正确答案:正确
第22题：

单选题
设函数y＝f（x）具有二阶导数，且f′（x）＝f（π/2－x），则该函数满足的微分方程为（　　）。
A
f″（x）＋f（x）＝0
B
f′（x）＋f（x）＝0
C
f″（x）＋f′（x）＝0
D
f″（x）＋f′（x）＋f（x）＝0

正确答案： A
解析：
由f′（x）＝f（π/2－x），两边求导得f″（x）＝－f′（π/2－x）＝－f[π/2－（π/2－x）]＝－f（x），即f″（x）＋f（x）＝0。
第23题：

单选题
如果奇函数f（x）在区间[a，b]（0＜a＜b）上是增函数，且最小值为2，那么f（x）在区间[－b，－a]上是（　　）．
A
增函数且最小值为－2
B
增函数且最大值为－2
C
减函数且最小值为－2
D
减函数且最大值为－2

正确答案： D
解析：
由于奇函数的图象关于坐标原点对称，借助图象（可作一草图，略），可知函数在原点两边定义域对称的范围内，其函数增减性一致．因此f（x）在[－b，－a]上也是增函数．而原点右边某一区间上的最大（小）值C，对称过去应为原点左边相应区间的最小（大）值－C．

设函数f（x）=x3-3x2-9x．求（I）函数f（x）的导数；（1I）函数f（x）在区间[1，4]的最大值与最小值．

题目

相似考题

参考答案和解析

更多“设函数f（x）=x3-3x2-9x．求（I）函数f（x）的导数；（1I）函数f（x）在区间[1，4]的最大值与最小值．”相关问题

相关内容