设的三条边分别是a，b，C，且a2+b2=c2。证明：ΔABC是直角三角形。(这是勾股定理的逆命题)

题目
设的三条边分别是a，b，C，且a2+b2=c2。证明：ΔABC是直角三角形。(这是勾股定理的逆命题)

相似考题

1.设λ1,λ2都是n阶矩阵A的特征值,λ1≠λ2,,且a1与a2分别是A的对应于λ1与λ2的特征向量,则().A.c1=0且c2=0时,a=c1a1+c2a2必是A的特征向量B.c1≠0且c2≠0时,a=c1a1+c2a2必是A的特征向量C.c1,c2=0时,a1=c1a1+c2a2必是A的特征向量D.c1≠0而c2=0时,a=c1a1+c2a2必是A的特征向量

2.一个等腰梯形有三条边的长度分别是 18 厘米、30 厘米、66 厘米，且下底是最长的一边。问这个等腰梯形的周长是多少厘米A.132 B.144 C.132或144 D.180

3.如右图，在梯形ABCD中，点E、F分别是腰AB、CD上的点． (1)证明：如果E、F为中点时，有 EF=1/2(AD+BC)； (2)请写出(1)中命题的逆命题，并判断该逆命题是否成立，若成立，请给予证明；若不成立，请说明理由．

4.已知点M是△ABC所在平面内的一点,且满足MA2+MB2+MC2=4,那么△ABC三条边长之积AB·BC·CA的最大值是____.

更多“设的三条边分别是a，b，C，且a2+b2=c2。证明：ΔABC是直角三角形。(这是勾股定理的逆命题) ”相关问题

  • 第1题：

    一个直角三角形的三条边分别是3厘米，4厘米，5厘米(如图)，如果以它的最长边为轴旋转一周，求旋转后所形成图形的体积.(π取3计算)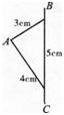


    答案：
    解析：



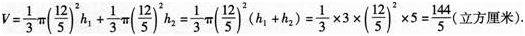
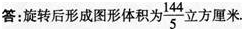
  • 第2题：

    设A1，A2分别为m阶，n阶可逆矩阵，分块矩阵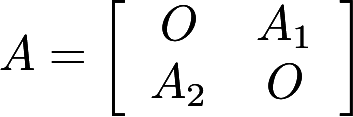.证明：A可逆，且


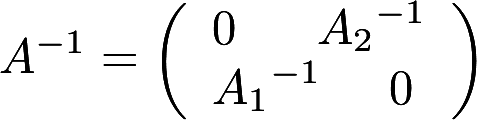    答案：
    解析：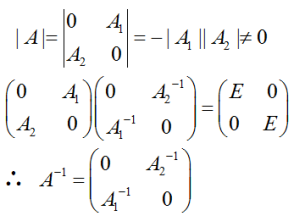

  • 第3题：

    设向量组α1,…,αn为两两正交的非零向量组,证明：α1,…,αn线性无关,并举例说明逆命题不成立.


    答案：
    解析：

  • 第4题：

    初中数学《勾股定理》
    一、考题回顾
    题目来源1月6日 下午 黑龙江省哈尔滨市 面试考题
    试讲题目1.题目：勾股定理
    2.内容：



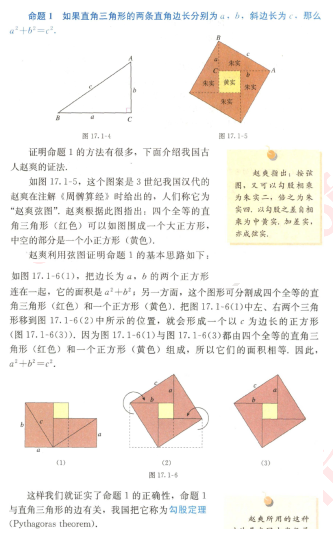
    3.基本要求：
    (1)要有板书;
    (2)试讲十分钟左右;
    (3)条理清晰，重点突出;
    (4)学生掌握勾股定理的证明方法。
    答辩题目1.勾股定理的教学过程中，体现了什么数学思想?
    2.常见的三组勾股数是什么?
    二、考题解析
    【教学过程】
    (一)引入新课
    出示“国际数学家大会会徽”，提出问题：会徽图案有什么特别的含义吗?蕴含什么样的数学奥秘?
    (二)探索新知
    活动1：出示“毕达哥拉斯朋友家地板砖图”。
    ?


    引导学生发现理解图形中全等的直角三角形的某种数量关系，并提出问题：等腰直角三角形三边长具有怎样的关系?引导学生利用面积规律整理归纳得出：等腰直角三角形两条直角边的平方和等于斜边的平方。
    问题1：一般的直角三角形是否也具有类似规律?引导学生在网格图利用面积探究规律并归纳出：直角三角形两条直角边的平方和等于斜边的平方。




    答案：
    解析：

  • 第5题：

    设P是3x3矩阵，其秩为2，考虑方程组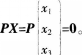
    (1)设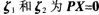的两个解C1、C2为实数，证明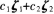也是PX=0的解；(4分)
    (2)方程组PX=0的解空间的维数是多少 (无需证明)(3分)


    答案：
    解析：
    (2)方程组PX=0的解空间的维数是未知量的个数n=3减去系数矩阵P的秩2，即为1。

  • 第6题：

    以下是某学生证明勾股定理“在Rt△ABC中，∠C=90°，求证a2+b2=c2”的过程：因为a=csinA，b=ccosA，所以a2+b2=c2sin2A+c2cos2A=c2(sin2A+cos2A)=c2。
    以上证明所犯的错误主要是( )。

    A.偷换论题
    B.虚假论据
    C.循环论证
    D.不能推出

    答案：C
    解析：
    该学生在论证中用到sin2A+cos2A=1，而这个公式成立依赖于a2+b2=c2，因此该学生的论证犯了循环论证的错误。

  • 第7题：

    勾股定理是由毕达哥拉斯学派最早提出证明，而勾股定理在中国称为什么定理？


    正确答案: 勾股定理、勾股弦定理、商高定理都可以

  • 第8题：

    护锥放样的勾股弦检查法，实际上是利用了（）的勾股定理。

    • A、矩形
    • B、平行四边形
    • C、直角三角形
    • D、双直线形

    正确答案:C

  • 第9题：

    填空题
    叶片式流体机械的速度三角形中有三条边，这三条边对应三个矢量，它们分别是（）、（）和（）矢量。

    正确答案： 绝对速度,相对速度,圆周速度（牵连速度）
    解析： 暂无解析

  • 第10题：

    单选题
    护锥放样的勾股弦检查法，实际上是利用了（）的勾股定理。
    A

    矩形

    B

    平行四边形

    C

    直角三角形

    D

    双直线形


    正确答案： C
    解析： 暂无解析

  • 第11题：

    单选题
    下列说法正确的个数有（　　）。①等边三角形有三条对称轴；②在△ABC中，若a2＋b2≠c2，则△ABC不是直角三角形；③等腰三角形的一边长为4，另一边长9，则它的周长为17或22；④一个三角形中至少有两个锐角。
    A

    1个

    B

    2个

    C

    3个

    D

    4个


    正确答案： B
    解析：
    ①④正确。②中若a2＋b2≠c2，则△ABC也可能是直角三角形，如当∠A或∠B是直角；③若两边长为4，则4＋4＜9，不能构成三角形，故周长不能为17。

  • 第12题：

    问答题
    勾股定理是由毕达哥拉斯学派最早提出证明，而勾股定理在中国称为什么定理？

    正确答案： 勾股定理、勾股弦定理、商高定理都可以
    解析： 暂无解析

  • 第13题：

    已知等腰直角三角形的三边长分别为abc,a,b为两条直角边.的值？

    A. 1006000
    B.503000
    C.2012
    D.20120

    答案：C
    解析：

  • 第14题：

    设A,B为同阶方阵, (1)若A,B相似,证明A,B 的特征多项式相等. (2)举一个二阶方阵的例子说明(1)的逆命题不成立. (3)当A,B均为实对称矩阵时,证明(1)的逆命题成立


    答案：
    解析：

  • 第15题：

    如图所示，ΔABC是直角三角形，四边形和四边形都是正方形，已知4cm，问正方形HFGF的面积是多少？（ ）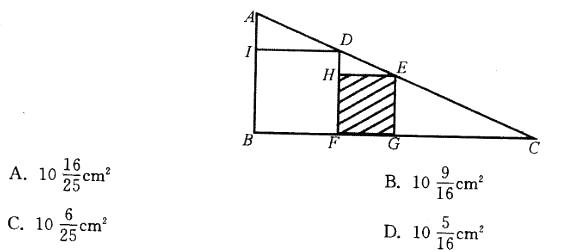


    答案：C
    解析：

  • 第16题：

    如图所示，ΔABC是直角三角形，四边形和四边形HFGE都是正方形，已知AI=1cm，IB=4cm，问正方形HFGE的面积是多少？（ ）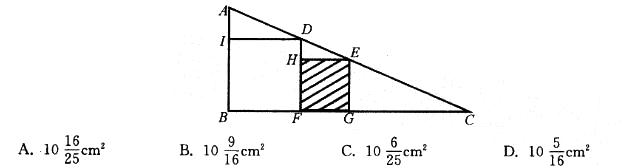


    答案：C
    解析：
    根据题意，AB = 5cm,ID=BF=4cm，我们利用比例关系“AI : ID = AB : BC”可得 BC=20cm,那么FC=BC-BF=16(cm)。我们假设EG=FG=xcm，那么GC=16-x，再利用比例关系"AB : BC=EG : GC”，得到5 : 20 = x : (16-x),解得x=3. 2，那么正方形HFGE 的面积为x2=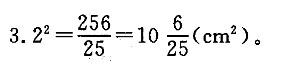

  • 第17题：

    直角三角形两直角边的平方和等于斜边的平方，这是平面几何的一条定理，下列选项中，不是用来指称这一定理的是( )。

    A.毕达哥拉斯定理
    B.欧几里得定理
    C.勾股定理
    D.商高定理

    答案：B
    解析：
    题干描述的是勾股定理的定义，勾股定理又称为商高定理或毕达哥拉斯定理。

  • 第18题：

    勾股定理表示的是直角三角形的二个直角边的平方和等于（）的平方。

    • A、斜边
    • B、另一直角边
    • C、高
    • D、对角线

    正确答案:A

  • 第19题：

    达芬奇用了（）组全等的四边形证明了勾股定理。

    • A、1
    • B、2
    • C、3
    • D、4

    正确答案:B

  • 第20题：

    勾股定理表示的是，直角三角形的两个直角边的平方和等于（）的平方。


    正确答案:斜边

  • 第21题：

    问答题
    以下是某高中信息技术教材中有关“用穷举法设计算法”的一部分：请用穷举法分析并解决下面的问题。在一个直角三角形中，三条边a，b，c的长度都为整数，且一条直角边a的长度已确定（例如为8），斜边c的长度不能超过某数I（例如100），找出满足条件的所有直角三角形。请就这一内容，完成下列任务： （1）简要分析该内容在教科书中的地位和作用。 （2）请说明本节课的教学重点和难点。

    正确答案： （1）本节介绍用穷举法求解问题，一个严密的穷举方案可以训练思维的严密和条理性，在应用计算机求解时，穷举算法也是一个常用的有效方法。通过本节内容的学习，学生对设计算法求解问题有了进一步的认识，对设计算法的步骤更加熟练，思考问题更加严密，程序编制和调试更有经验。本节的学习对算法知识的积累，对继续学习的激发有更加强烈的愿望。
    （2）教学重点：建立正确的数学模型，确定穷举方案。教学难点：针对具体问题确定穷举方案。
    解析： 暂无解析

  • 第22题：

    填空题
    西方最早证明勾股定理的是（）

    正确答案： 毕达哥拉斯
    解析： 暂无解析

  • 第23题：

    单选题
    达芬奇用了（）组全等的四边形证明了勾股定理。
    A

    1

    B

    2

    C

    3

    D

    4


    正确答案： B
    解析： 暂无解析

相关内容