若A,口是正交矩阵,则下列说法错误的是( )。 A、AB为正交矩阵 B、A+B为正交矩阵 C、A-1B为正交矩阵 D、AB-1为正交矩阵
题目
若A,口是正交矩阵,则下列说法错误的是( )。
A、AB为正交矩阵
B、A+B为正交矩阵
C、A-1B为正交矩阵
D、AB-1为正交矩阵
B、A+B为正交矩阵
C、A-1B为正交矩阵
D、AB-1为正交矩阵
相似考题
更多“若A,口是正交矩阵,则下列说法错误的是( )。 ”相关问题
-
第1题:
n阶正交矩阵的乘积是()矩阵。A、单位
B、对称
C、实
D、正交
参考答案:D
-
第2题:
设A,B为n阶矩阵,则下列结论正确的是().A.若A,B可逆,则A+B可逆
B.若A,B可逆,则AB可逆
C.若A+B可逆,则A-B可逆
D.若A+B可逆,则A,B都可逆答案:B解析:若A,B可逆,则|A|≠0,|B|≠0,又|AB|=|A||B|,所以|AB|≠0,于是AB可逆,选(B). -
第3题:
设A,B为n阶矩阵,考虑以下命题:①若A,B为等价矩阵,则A,B的行向量组等价②若行列式.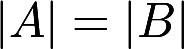 ,则A,B为等价矩阵③若
,则A,B为等价矩阵③若 与
与 都只有零解,则A,B为等价矩阵④若A,B为相似矩阵,则
都只有零解,则A,B为等价矩阵④若A,B为相似矩阵,则 与
与 的解空间的维数相同以上命题中正确的是( ).
A.①③
的解空间的维数相同以上命题中正确的是( ).
A.①③
B.②④
C.②③
D.③④答案:D解析:
-
第4题:
设A,B是可逆矩阵,且A与B相似,则下列结论错误的是
 答案:C解析:
答案:C解析:
-
第5题:
若A是实对称矩阵,则A为正定矩阵的充要条件是A的特征值全为正答案:对解析: -
第6题:
证明下列命题:(1) 若A,B是同阶可逆矩阵,则(AB)*=B*A*.(2) 若A可逆,则A*可逆且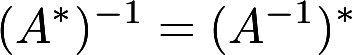 .(3) 若AA′=E,则.
.(3) 若AA′=E,则.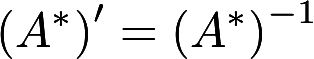 答案:解析:
答案:解析:
-
第7题:
下列说法中错误的是( )。A.同频率正弦量之间的相位差与频率密切相关
B.若电压与电流取关联参考方向,则感性负载的电压相量滞后其电流相量90°
C.容性负载的电抗为正值
D.若某负载的电压相量与其电流相量正交,则该负载可以等效为纯电感或纯电容答案:A,B,C解析:同频率正弦量的相位差仅与初相位有关。若电压与电流取关联参考方向,感性负载电压超前电流。容性负载的电抗为负值。纯电感电压超前电流90°,纯电容电流超前电压90°。 -
第8题:
下面4个矩阵中,不是正交矩阵的是( ).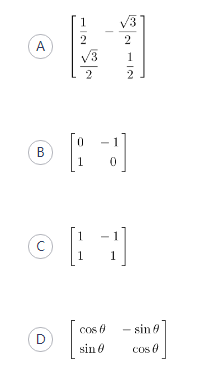 答案:C解析:
答案:C解析:
-
第9题:
若A,B是正交矩阵,则下列说法错误的是()。
- A、AB为正交矩阵
- B、A+B为正交矩阵
- C、ATB为正交矩阵
- D、AB-1为正交矩阵
正确答案:B -
第10题:
设A,B,C均为非零二阶矩阵,则下列各式正确的是()。
- A、AB=BA
- B、(AB)C=A(BC)
- C、若AB=0,则A=0或B=0
- D、若AB=C,则B=CA-
正确答案:B -
第11题:
填空题若图的邻接矩阵是对称矩阵,则该图一定是()。正确答案: 无向图解析: 暂无解析 -
第12题:
单选题若A,B是正交矩阵,则下列说法错误的是()。AAB为正交矩阵
BA+B为正交矩阵
CATB为正交矩阵
DAB-1为正交矩阵
正确答案: A解析: 由正交矩阵的定义可知,若A,B正交,则有ATA=I(I为单位阵),BTB=I,则(AB)T(AB)=BTATAB=I,则选项A正确,同理可证明选项C、D也是正交矩阵。而选项B,(A+B)T(A+B)=(AT+BT)(A+B)=2I+BTA+ATB,显然不正确,故选B。 -
第13题:
若A是实对称矩阵,则若|A|>O,则A为正定的答案:错解析: -
第14题:
若A是实对称矩阵,则A的特征值全为实数答案:对解析: -
第15题:
设N阶矩阵A与对角矩阵合同,则A是().A.可逆矩阵
B.实对称矩阵
C.正定矩阵
D.正交矩阵答案:B解析:
-
第16题:
设A为n阶矩阵,A^2=A,则下列结论成立的是().A.A=O
B.A=E
C.若A不可逆,则A=O
D.若A可逆,则A=E答案:D解析:因为A^2=A,所以A(E-A)=O,由矩阵秩的性质得,r(A)+r(E—A)=n,若A可逆,则r(A)=n,所以r(E-A)=0,A=E,选(D). -
第17题:
若矩阵A= ,B是三阶非零矩阵,满足AB=O,则t=_______.答案:1、1解析:由AB=0得r(A)+r(B)≤3,因为r(B)≥1,所以r(A)≤2,又因为矩阵A有两行不成比例,所以r(A)≥2,于是r(A)=2.
,B是三阶非零矩阵,满足AB=O,则t=_______.答案:1、1解析:由AB=0得r(A)+r(B)≤3,因为r(B)≥1,所以r(A)≤2,又因为矩阵A有两行不成比例,所以r(A)≥2,于是r(A)=2.
由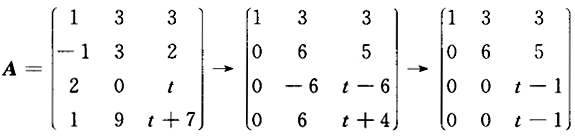 得t=1.
得t=1. -
第18题:
设A与B都是n阶正交矩阵,证明AB也是正交矩阵.答案:解析: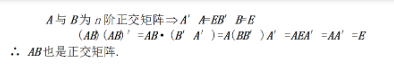
-
第19题:
下面4个矩阵中,不是正交矩阵的是( )。
A.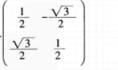
B.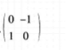
C.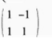
D.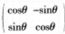 答案:C解析:A为n阶矩阵,
答案:C解析:A为n阶矩阵,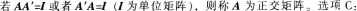
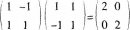 结果不是单位矩阵。故选C。
结果不是单位矩阵。故选C。 -
第20题:
设A是3阶矩阵,P = (α1,α2,α3)是3阶可逆矩阵,且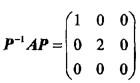 ,若矩阵Q=(α2,α1,α3),则Q-1AQ=( )。
,若矩阵Q=(α2,α1,α3),则Q-1AQ=( )。
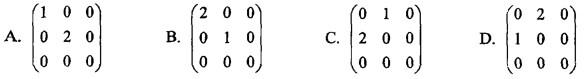 答案:B解析:提示:由条件知,λ1=1,λ2=2,λ3=0是矩阵A的特征值,而α1,α2,α3是对应的特征向量,故有
答案:B解析:提示:由条件知,λ1=1,λ2=2,λ3=0是矩阵A的特征值,而α1,α2,α3是对应的特征向量,故有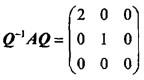 。
。 -
第21题:
设A,B都是n阶矩阵,若有可逆矩阵P使得P-1AP=B,则称矩阵A与矩阵B()。
- A、等价
- B、相似
- C、合同
- D、正交
正确答案:B -
第22题:
若图的邻接矩阵是对称矩阵,则该图一定是()。
正确答案:无向图 -
第23题:
单选题设A,B都是n阶矩阵,若有可逆矩阵P使得P-1AP=B,则称矩阵A与矩阵B()。A等价
B相似
C合同
D正交
正确答案: B解析: 由相似矩阵的定义知B正确。故选B。
