：某大学某班学生总数为32人。在第一次考试中有26人及格，在第二次考试中有24人及格。若两次考试中，都没有及格的有4人，那么两次考试都及格的人数是（ ）。A．22 B．18C．28 D．26
题目
：某大学某班学生总数为32人。在第一次考试中有26人及格，在第二次考试中有24人及格。若两次考试中，都没有及格的有4人，那么两次考试都及格的人数是（ ）。
A．22 B．18
C．28 D．26
相似考题
参考答案和解析
由题意知第一次不及格的有6人，第二次不及格的有8人，又已知两次都不及格的人有4人，则两次考试刚好及格一次的人数为6＋8－4＝10（人），则两次都及格的人数为32－（6＋8－4）＝22（人），故答案为A。
更多“:某大学某班学生总数为32人。在第一次考试中有26人及格,在第二次考试中有24人及格。若两次考 ”相关问题
-
第1题：
某大学某班学生总数为32人，在第一次考试中有26人及格，在第二次考试中有24人及格，若两次考试中，都没有及格的有4人，那么两次考试都及格的人数是( )。
A．22
B．18
C．28
D．26
正确答案：A
A [解析]都没有及格的有4人，则至少有一次考试及格的人数为32-4=28，两次考试及格的总人数次是26+24=50，所以两次考试都及格的人数是50-28=22，故选A。
-
第2题：
某班有40人，在期末考试中，语文有35人及格，数学有32人及格，外语有33人及格，不及格的人中没有只有一门不及格的，其中有2人全都不及格，有4人语文和数学都不及格，有6人数学和外语都不及格，有多少人语文和外语都不及格?（ ）
A．2
B．3
C．4
D．5
正确答案：B
(1)全班共40人。(2)设语文和外语都不及格的为X人。由于有4人语文和数学都不及格的减去2个都不及格的，有2个仅语文和数学不及格而外语及格，由于语文和外语都不及格的为％人，减去2个都不及格的为(x－2)个仅语文和外语不及格而数学及格的，全班共40人，即40=35+2+(x－2)+2，解得x=3，故选B。 -
第3题：
六年级一班有学生50人，第一次考试有38人及格，第二次考试有24人及格，其中两次考试都及格的有20人，两次考试都不及格的有多少人：
A6
B12
C8
D10答案：C解析：由两集合容斥原理公式得两次都不及格的人数为50-(38+24-20)=8人。故正确答案为C。
两集合容斥原理公式：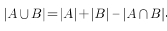
-
第4题：
某班40名学生统计学考试成绩（分）分别为：
学校规定：60分以下为不及格，60─70分为及格，70─80分为中，80─90分为良，90─100分为优。 指出分组标志及类型；分析该班学生考试情况。
分组标志是“成绩”，其类型是数量标志，分组方法：是变量分组中的组距式分组，而且是开口分组；本班学生考试的成绩分布呈“两头小，中间大”的“正态分布”。
略 -
第5题：
下列判断与“这次考试可能会及格”为矛盾关系判断的有（）。
- A、这次考试可能不会及格
- B、这次考试必然不及格
- C、这次考试不必然会及格
- D、这次考试不可能不及格
正确答案:B -
第6题：
特殊培训考试分理论考试和实际操作考试。理论考试和实际操作考试（）视为考试合格。
- A、理论考试及格
- B、任一项考试及格
- C、两项考试均及格
正确答案:C -
第7题：
当判断（）为真时，判断“班上同学考试都及格”为假。
- A、并非班上同学考试都不及格
- B、班上同学考试不都及格
- C、班上没有一个同学考试不及格
- D、并非班上有的同学考试及格
- E、班上同学考试不都不及格
正确答案:B,D -
第8题：
哪一项最能削弱“„甲班在此次期末考试各科成绩均及格”这一结论？（）
- A、甲班学生王武在考试中有一门课程不及格
- B、甲班学生李思沉迷网络，学习成绩急剧下降
- C、张珊不是甲班学习成绩最差的
- D、考试成绩不能成为评价学生的唯一标准
正确答案:A -
第9题：
单选题下列判断与“这次考试可能会及格”为矛盾关系判断的有（）。A这次考试可能不会及格
B这次考试必然不及格
C这次考试不必然会及格
D这次考试不可能不及格
正确答案： B解析： 暂无解析 -
第10题：
单选题Jack 读小学二年级，一次考试中有一门功课不及格，经过补习之后第二次考试仍然不及格，他很可能会产生（）心理。A自卑
B怀疑
C羞怯
D内疚
正确答案： A解析： 7—12岁 学龄期 获得勤奋感克服自卑感 体验能力的实现 -
第11题：
多选题当判断（）为真时，判断“班上同学考试都及格”为假。A并非班上同学考试都不及格
B班上同学考试不都及格
C班上没有一个同学考试不及格
D并非班上有的同学考试及格
正确答案： B,A解析： 暂无解析 -
第12题：
问答题39.在一次考试中，某班学生数学和外语的及格率都是0.7．且这两门课是否及格相互独立．现从该班任选一名学生，则该生数学和外语只有一门及格的概率为正确答案：解析： -
第13题：
如果小张考试及格并且大田考试不及格，则小娜考试一定不及格。如果以上命题是真的，那么，再加上什么前提，可以得出结论：大田考试及格了（ ）
A．小张考试及格而大田考试不及格
B．小张与小娜考试都不及格
C．小张与小娜考试都及格了
D．小张考试不及格而小娜考试及格
正确答案：C题干是以一个充分条件假言命题“如果p并且非q，那么非r”作前提得出结论“q”，需要补充前提。观察题干可以发现，结论“q”是充分条件的前件中的一部分内容。充分条件假言推理通过否定后件可以得到关于前件内容的否定，因此，首先应该否定后件“非r”，即非非r，也即r，“小娜考试及格了”，可以得到，并非“p并且非q”，即“非p或者q”，“小张没有及格或者大田及格了”，这是一个选言命题，它的有效推理式是否定肯定式，即通过否定一个选言支(即非非p)来肯定另一个选言支(即q)，要想肯定“大田及格了”必须否定“小张没有及格”，即“小张及格了”；所以，要想得到“大田及格了”的结论，需要补充“小娜及格了”和“小张及格了”，即选项C。 -
第14题：
某班共有50名学生参加数学和外语两科考试，已知数学成绩及格的有40人，外语成绩及格的有25人，据此可知数学成绩及格而外语成绩不及格者（ ）
正确答案：B
-
第15题：
某班学生不到50人，在一次考试中，有1/7人得优，1/3人得良，1/2人及格，其余的均不及格，那么不及格的人数是（ ）。
A. 1
B. 2
C. 3
D. 4答案：A解析：解题指导： 通过题干可知，该班级最少人数应为7、3、2的最小公倍数，又因为不能超过50人，所以该班人数为7×3×2=42人。那么不及格的人数为1。故答案为A。 -
第16题：
当命题（）为真时，命题“班上同学考试都及格”为假。
- A、并非班上同学考试都不及格
- B、班上有的同学考试不及格
- C、班上同学并没都及格
- D、班上同学都不及格
- E、并非班上有的同学考试及格
正确答案:B,C,D,E -
第17题：
申领民用航空器活动区机动车驾驶证的人员在考试中有舞弊行为的，将取消考试资格。理论考试和道路考试均为（）分及格。
- A、60
- B、70
- C、80
- D、90
正确答案:D -
第18题：
某班有学生50人，有26人在第一次考试中得优，有21人在第二次考试中得优，有17人在两次考试中都没有得优，那么两次考试都得优的学生人数是（）
- A、11.0
- B、12.0
- C、13.0
- D、14.0
正确答案:D -
第19题：
如果在一次考试中，某班学生数学和外语的及格率都是0.7，且这两门课是否及格相互独立，现从该班任选一名学生，则该生数学和外语只有一门及格的概率为0.42
正确答案:正确 -
第20题：
当判断（）为真时，判断“班上同学考试都及格”为假。
- A、并非班上同学考试都不及格
- B、班上同学考试不都及格
- C、班上没有一个同学考试不及格
- D、并非班上有的同学考试及格
正确答案:B,D -
第21题：
多选题当判断（）为真时，判断“班上同学考试都及格”为假。A并非班上同学考试都不及格
B班上同学考试不都及格
C班上没有一个同学考试不及格
D并非班上有的同学考试及格
E班上同学考试不都不及格
正确答案： B,C解析： “班上同学考试都及格”为假即SAP为假。 A、“并非班上同学考试都不及格”等值于SIP而SIP真SAP是可真可假所以错误； B、是一个SEP判断，由于SEP与SAP是不能同真所以SEP真即可断定SAP假所以正确； C、实际上就是一个SAP判断所以错误； D、等值于SEP与B相同所以正确； E、实际上是一个SAP判断所以错误。所以应选BD。 -
第22题：
单选题通常百分制规定60分以上及格，以下则不及格。某班化学考试，若全班都60分以上，则全班及格，若全班都60分以下，则都不及格，这种评价称为（）。A绝对评价
B相对评价
C个体内差异评价
D标准化评价
正确答案： C解析： 相对评价是为了对每个个体在群体所处的相对位置作出区分而进行的评价；绝对评价是对每一个评价对象达成目标程度作出的判断；个体内差异评价是以评价对象自身状况为基准，就自身的发展情况进行纵向或横向比较而作出的判断。 -
第23题：
多选题当命题（）为真时，命题“班上同学考试都及格”为假。A并非班上同学考试都不及格
B班上有的同学考试不及格
C班上同学并没都及格
D班上同学都不及格
E并非班上有的同学考试及格
正确答案： C,D解析： 暂无解析
学校规定：60分以下为不及格，60─70分为及格，70─80分为中，80─90分为良，90─100分为优。 指出分组标志及类型；分析该班学生考试情况。