甲、乙二人各走一段路，已知他们走路的时问比为3：4，速度比为7：5，则他们所走路程比为（ ）。A．21：20B．10：9C．28：15D．15：28

题目

甲、乙二人各走一段路，已知他们走路的时问比为3：4，速度比为7：5，则他们所走路程比为（ ）。

A．21：20

B．10：9

C．28：15

D．15：28

相似考题

1.甲、乙两仓库存货吨数比为4：3，如果由甲库中取出8吨放到乙库中，则甲、乙两仓库存货吨数比为4：5。两仓库原存货总吨数是多少?（ ）A．94B．87C．76D．63

2.甲、乙两物体都作匀速直线运动，已知甲、乙两物体运动时间之比4：5，通过的路程之比为3：2，则甲、乙两物体运动速度之比为（ ）A．6：5B．15：8C．5：6D．8：15

3.甲、乙两列车分别从A、B两站同时相向开出，已知甲车速度与乙车速度的比为3:2，C站在A、B两站之间。甲、乙两列车到达C站的时间分别是早晨5时和下午3时。则甲、乙两车相遇的时间是( ) 。A．早晨7时B．上午9时C．上午11时D．下午1时

4.甲、乙两人有一定数量的苹果，若甲给乙39个苹果后两人苹果数量之比为5：7；若甲给乙44个苹果后两人苹果数量之比为3：5。问甲、乙共有多少个苹果? A．132 B．104 C．120 D．124

更多“甲、乙二人各走一段路,已知他们走路的时问比为3:4,速度比为7:5,则他们所走路程比为()。 ”相关问题

  • 第1题：

    甲、乙二人各走一段路，已知他们走路的时间比为3:4，速度比为7:5，则他们所走路程比为（ ）。

    A．21:20

    B．10:9

    C．28:15

    D．15:28


    正确答案：A
    二人路程比为：(3×7)：(4×5)一21：20。正确答案为A。

  • 第2题：

    甲、乙、丙三篮子中共有苹果57个，已知甲篮子的苹果数比乙多6个，丙篮子的苹果数比乙少3个，则甲、乙、丙三个篮子中的苹果数之比为：( )

    A.9：7：6
    B.8：6：5
    C.5：4：3
    D.5：3：2

    答案：B
    解析：
    设乙篮子的苹果数为x，则甲的为x+6，丙的为x-3。由题意知，(x+6)+x+(x-3)=57，解得x=18。则所求为(18+6)：18：(18-3)=8：6：5，B正确。

  • 第3题：

    甲乙两船分别从上游和下游同时出发，甲顺流而下，乙逆流而上，相遇时甲乙走过的路程之比为3:1，两船相遇后各自立即掉头沿原路返回，甲、乙各自返回到出发点所用时间之比为5:1。设船速和水流速度均不变，则甲船速度与乙船速度的比值是：


    答案：C
    解析：
    甲乙两船相遇时，所用时间相同，路程比为3:1，返回时路程比不变，时间比为5:1，由此可得方程组：

  • 第4题：

    小王和小刘两人分别从甲镇和乙镇同时出发，匀速相向而行，1小时后他们在甲镇和乙镇 之间的丙镇相遇，相遇后两人继续前进，小刘在小王到达乙镇之后27分钟到达甲镇，那么小王和小刘的速度之比为：

    A. 5:4
    B. 6:5
    C. 3:2
    D. 4:3

    答案：A
    解析：
    行程问题，代入排除法；
    将选项A代入，速度比为5:4，假设小王速度为5，小刘速度为4，一个小时相遇，所以，路程甲丙=5，乙丙=4，，相遇后，小王到乙时间=4/5小时=48分钟，小刘到甲时间为5/4小时=75分钟，时间差为27分钟。符合题意，所以答案选A。

  • 第5题：

    某企业在软件园区的分公司有甲、乙2个开发团队。现从乙团队调走25人，此时甲、乙团队人数比为4∶3。然后又从甲团队调走42人，此时甲、乙团队人数之比2∶5。问两次调动之前，甲、乙团队人数比为：

    A.3∶4
    B.6∶7
    C.1∶2
    D.2∶5

    答案：B
    解析：
    第一步，本题考查基础应用题。
    第二步，设第一次调动后甲团队的人数为4x，则乙的人数为3x，根据第二次调动可得（4x－42）∶3x＝2∶5，解得x＝15。
    第三步，在两次调动前，甲团队的人数是4×15＝60（人），乙团队的人数是3×15＋25＝70（人），故甲、乙两队人数之比为6∶7。

  • 第6题：

    如图所示，有一固定且内壁光滑的半球面，球心为O，最低点为O/，在其内壁上有两个质量相同，可视为质点的小球甲和乙，分别在高度不同的水平面内做匀速圆周运动，若甲乙两球与O点的连线与竖直线00/’间的夹角分别为α＝53。和β＝370，则( )。(已知 sin370＝3/5，cos370＝4/5；sin530＝4/5,cos530＝3/5)



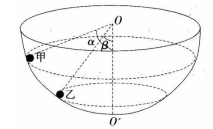    A．甲、乙两球运动周期之比为3／4
    B．甲、乙两球所受支持力大小之比为3／4
    C．甲、乙两球运动周期之比为3/41/2
    D．甲、乙两球所受支持力大小之比为3/41/2

    答案：C
    解析：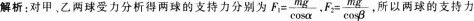

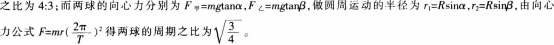
  • 第7题：

    甲、乙、丙的速度之比为3∶4∶5，经过相同的一段路，三人所用时间之比：（）

    • A、3：4：5
    • B、5：4：3
    • C、20：15：12
    • D、12：8：5

    正确答案:C

  • 第8题：

    相同材料制成的两个均匀导体，长度之比为3：5，横截面积之比为4：1，则其电阻之比为（）。

    • A、12：5
    • B、3：20
    • C、7：6
    • D、20：3

    正确答案:B

  • 第9题：

    填空题
    甲、乙两辆拖拉机的功率相等，沿不同的路面运动，如果在相同的时间内通过的路程之比为4：3，那么，两辆拖拉机完成功的比值为____，甲、乙两车的牵引力之比为____.

    正确答案： 1:1,3:4
    解析：
    功等于功率乘时间，功还等于力乘以距离．

  • 第10题：

    单选题
    某企业在软件园区的分公司有甲、乙两个开发团队，先从乙团队调走25人，此时甲、乙团队人数比为4:3.然后又从甲团队调走42人，此时甲、乙团队人数比为2:5，则两次调动前甲、乙团队人数比力：
    A

    3:4

    B

    6:7

    C

    1:2

    D

    2:5


    正确答案： B
    解析：

  • 第11题：

    单选题
    两跟同种材料的电阻丝，长度之比为1：5，横截面积之比为2：3，则它们电阻之比为（）。
    A

    4：10

    B

    3：10

    C

    1：3

    D

    2：7


    正确答案： B
    解析： 暂无解析

  • 第12题：

    单选题
    甲、乙、丙的速度之比为3∶4∶5，经过相同的一段路，三人所用时间之比：（）
    A

    3：4：5

    B

    5：4：3

    C

    20：15：12

    D

    12：8：5


    正确答案： C
    解析： 路程相同时，速度与时间成反比，因此，经过相同的路程，甲、乙、丙的时间比为1/3∶1/4∶1/5=20∶15∶12。

  • 第13题：

    甲乙丙三箱水果，甲与乙的重量之比为3：4，甲与丙的重量之比为5：2，从乙箱取4千克放入丙箱，乙丙重量之比为9：4，则甲、乙、丙三箱重量之和为多少千克? A．40 B．82 C．80 D．70


    正确答案：B
    由题意可知，甲：乙：丙=15：20：6，乙、丙重量比为20：6=10：3。乙丙一共有10+3=13份．置换后重量之比为9：4，依旧是13份。因此乙减少的一份为4千克。所以乙、丙共有13x4=52千克，甲有52÷(20+6)×15=30千克。故共有52+30=82千克。

  • 第14题：

    某单位男女员工的人数之比是15∶13。按人数之比5∶7∶8，分为甲、乙、丙三个科室。其中甲科室男女员工的人数之比为4∶3，乙科室为5∶2。则丙科室男女员工人数之比为：

    A.1∶2
    B.2∶3
    C.5∶9
    D.5∶8

    答案：C
    解析：
    第一步，本题考查基础应用题，用赋值法解题。
    第二步，根据男女比为15∶13，则总人数应该为28的倍数；又因为甲∶乙∶丙＝5∶7∶8，则总人数应该为20的倍数；所以赋值总人数为140，则男生人数为75，女生人数为65。甲＝35，乙＝49，丙＝56。又因为甲科室的男女比为4∶3，则甲的男生为20，甲的女生为15，又因为乙科室的男女比为5∶2，则乙的男生为35，乙的女生为14，所以得出丙的男生为75－20－35＝20，丙的女生为65－15－14＝36，则丙的男女比＝20∶36＝5∶9。

  • 第15题：

    某街道常住人口与外来人口之比为1:2，已知该街道下辖的甲、乙、丙三个社区人口比为12:8:7。其中，甲社区常住人口与外来人口比为1:3，乙社区为3:5，则丙社区常住人口与外来人口比为：

    A.1:2
    B.1:3
    C.2:3
    D.3:4

    答案：D
    解析：
    设甲、乙、丙三个社区的人口分别为12、8、7，则该街道共有12+8+7=27人。列表如下：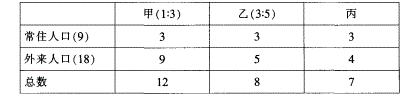
    所以，丙社区常住人口与外来人口的比为3:4。

  • 第16题：

    甲、乙两仓库存货吨数比为4 : 3，如果由甲库中取出8吨放到乙库中，则甲、乙两仓库存货 吨数比为4 : 5。两仓库原存货总吨数是（ ）。
    A. 94 B. 87 C. 76 D. 63


    答案：D
    解析：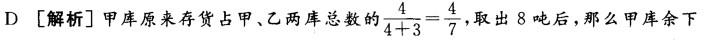


  • 第17题：

    如图所示，有一个固定且内壁光滑的半球面，球心为0，最低点为O′，在其内壁上有两个质量相同、可视为质点的小球甲和乙，分别在高度不同的水平面内做匀速圆周运动，若甲乙两球与O点的连线与竖直线O0′的夹角分别为α=53°和β=37°，则 (已知sin37°=3/5，cos37°=4/5，sin53°=4/5，cos53°=3/5)


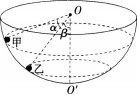    A．甲、乙两球运动周期之比为3／4

    B．甲、乙两球运动周期之比为√3/4

    C．甲、乙两球所受支持力之比为3／4

    D．甲、乙两球所受支持力之比为√3/4

    答案：B
    解析：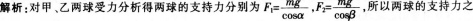

  • 第18题：

    下列说法正确的有：（）

    • A、小张与小王两人跑步，这两个人的速度之比是5∶6，两人都跑了55分钟，那么两个人跑步的路程之比是5∶6
    • B、一项工程，甲单独6个小时完成，乙单独8个小时完成，则甲乙完成这项工程的效率之比为3∶4
    • C、甲乙丙三人从A地到B地，他们的速度之比1∶2∶3，那么他们所用的时间之比是3∶2∶1
    • D、A部门花2万元买电脑，B部门花3万元买电脑，已知A部门与B部门购买的电脑数量之比是4∶7，那么两个部门买的电脑的单价之比为7∶4

    正确答案:B

  • 第19题：

    一项工作，甲、乙合作20小时可以完成，已知甲与乙的速度比为5：4，则甲单独完成这项工作需要的小时数为（）。

    • A、45
    • B、40
    • C、39
    • D、36

    正确答案:D

  • 第20题：

    单选题
    某企业在软件园区的分公司有甲、乙两个开发团队，先从乙团队调走25人，此时甲、乙团队人数比为4:3，然后又从甲团队调走42人，此时甲、乙团队人数比为2：5，则两次调动前甲、乙团队人数比为：
    A

    3:4

    B

    6:7

    C

    1:2

    D

    2:5


    正确答案： A
    解析：

  • 第21题：

    单选题
    一项工作，甲、乙合作20小时可以完成，已知甲与乙的速度比为5：4，则甲单独完成这项工作需要的小时数为（）。
    A

    45

    B

    40

    C

    39

    D

    36


    正确答案： B
    解析： 工程问题--比例法。甲与乙的速度比为5：4，则甲与甲、乙合作速度比为5：9，则甲单独完成的时间与甲、乙合作完成时间比为9：5；甲、乙合作20小时可以完成，则甲单独完成所用时间为20÷5÷9=36小时，故选D。

  • 第22题：

    单选题
    下列说法正确的有：（）
    A

    小张与小王两人跑步，这两个人的速度之比是5∶6，两人都跑了55分钟，那么两个人跑步的路程之比是5∶6

    B

    一项工程，甲单独6个小时完成，乙单独8个小时完成，则甲乙完成这项工程的效率之比为3∶4

    C

    甲乙丙三人从A地到B地，他们的速度之比1∶2∶3，那么他们所用的时间之比是3∶2∶1

    D

    A部门花2万元买电脑，B部门花3万元买电脑，已知A部门与B部门购买的电脑数量之比是4∶7，那么两个部门买的电脑的单价之比为7∶4


    正确答案： B
    解析： 暂无解析

  • 第23题：

    单选题
    某企业在软件园区的分公司有甲、乙2个开发团队，现从乙团队调走25人，此时甲、乙团队人数比为4:3，然后又从甲团队调走42人，此时甲、乙团队人数比为2:5。问两次调动之前，甲、乙团队人数比为：
    A

    3:4

    B

    6:7

    C

    1:2

    D

    2:5


    正确答案： B
    解析：

相关内容