:一篇文章 ,现有甲乙丙三人,如果由甲乙两人合作翻译,需要 10 小时完成,如果由乙丙两人合作翻译,需要12 小时完成。现在先由甲丙两人合作翻译4 小时,剩下的再由乙单独去翻译,需要12 小时才能完成,则,这篇文章如果全部由乙单独翻译,要( ) 小时能够完成.A.15 B . 18 C . 20 D .25
题目
:一篇文章 ,现有甲乙丙三人,如果由甲乙两人合作翻译,需要 10 小时完成,如果由乙丙两人合作翻译,需要12 小时完成。现在先由甲丙两人合作翻译4 小时,剩下的再由乙单独去翻译,需要12 小时才能完成,则,这篇文章如果全部由乙单独翻译,要( ) 小时能够完成.
A.15 B . 18 C . 20 D .25
相似考题
参考答案和解析
熟悉的工程问题,我们小时侯不知道做了多少遍。假设甲乙丙单独完成分别需要abc小时。
1/a+1/b=1/10(1)
1/b+1/c=1/12(2)
(1/c+1/a)×4+12/b=1(3)
由(3)可以得
1/a+1/c=1/4-3/b(4)
(1)+(2)得1/a+1/c+2/b=1/10+1/12(5)
把(4)带入(5)消去1/a+1/c得b=15。所以,答案为A15。这样计算显然相当烦琐。有没有简洁的方法呢?实际上每一道题目都有简单的
方法。
简便方法如下:
乙丙合作12小时完成;甲丙两人合作翻译4 小时,剩下的再由乙单独去翻译,需要12 小时才能完成。
假设甲每小时的工作量为X,乙为Y,丙为Z。那么总工作量可以表示为 12Y+12Z,也可以表示为4X+4Z+12Y。
12Y+12Z=4X+4Z+12Y。X=2Z也就是说丙2小时的工作量相当于甲1小时的工作量。
甲乙两人合作翻译,需要10 小时完成;如果由乙丙两人合作翻译,需要12 小时完成。由于丙12小时的工作量相当于甲6小时的工作量,我们可以得出这样的结论:甲乙两人合作翻译,需要10 小时完成;甲工作6小时后,乙接着工作12小时也可以完成。这个工作量可以表示为
10x+10y,也可以表示为6x+12y。10X+10Y=12Y+12Z=12Y+6X得到Y=2X。
也就是说甲2小时的工作量相当于乙1小时的工作量。
因为,甲乙两人合作翻译,需要10 小时完成该工作。甲10小时的工作量相当于乙5小时的工作量。因此乙单独做需要15小时完成。
两种方法对比,发现利用工作量来解决这个问题比较迅速。能够避免烦琐的计算。
更多“:一篇文章 ,现有甲乙丙三人,如果由甲乙两人合作翻译,需要 10 小时完成,如果由乙丙两人合作 ”相关问题
-
第1题:
:一篇文章,现有甲乙丙三人,如果由甲乙两人合作翻译,需要10小时完成,如果由乙丙两人合作翻译,需要12小时完成,现在先由甲丙两人合作翻译4小时,剩下的再由乙单 独去翻译,需要12小时才能完成,则,这篇文章如果全部由乙单独翻译,需要( )小时能够完成。
A.15
B.18
C.20
D.25
正确答案:A本题属于工程问题。设甲、乙、丙三人单独完成全部翻译分别需要x、y、z小时完成,如果再设总任务为1,则由题意可得:
由此可解得b=1/15,所y=15,即乙单独完成全部翻译需要15小时。
-
第2题:
一件工程,甲乙两人合作36小时完成,乙丙两人合作45小时完成,甲丙两人合作要60小时完成,问甲单独做需要多少小时完成?
A.72
B.75
C.81
D.90答案:D解析:我们设总的工作量是天数的最小公倍数,即180(36、45、60的最小公倍数),同时,设甲乙丙的工作效率分别是XYZ。题目说“甲乙两人合作36天完成”,说明甲乙合作一天的效率就是5(180÷36),根据“乙丙两人合作45天完成”,说明乙丙合作一天的效率就是4(180÷45),根据“甲丙两人合作要60天完成”,说明甲丙合作一天的效率就是3(180÷60)。所以可以列方程:
X+Y=5,Y+Z=4,X+Z=3
解方程得:X=2,也就是甲单独做的工作效率是2,那么已知总的工作量为180,所以甲独 做需要90(180÷2)天完成。 -
第3题:
一篇文章,现有甲乙丙三人,如果由甲乙两人合作翻译,需要10小时完成,如果由乙丙两人合作翻译,需要12小时完成,现在先由甲丙两人合作翻译4小时,剩下的再由乙单 独去翻译,需要12小时才能完成,则,这篇文章如果全部由乙单独翻译,需要( )小时能够完成。
A.15
B.18
C.20
D.25答案:A解析:【参考解析】: 本题属于工程问题。设甲、乙、丙三人单独完成全部翻译分别需要x、y、z小时完成,如果再设总任务为1,则由题意可得: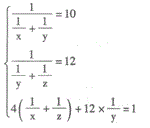
这是一个复杂的方程组,为了解题方便可以设1/x=a,1/y=b,1/z=c,则可得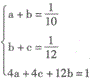
由此可解得b=1/15,所y=15,即乙单独完成全部翻译需要15小时。 -
第4题:
完成一项任务 ,甲乙两人所需工时相同。如果两人合作完成该任务,可以比计划工时提前5个小时完成。如果两人先合作,- -起工作6小时后雨由乙单独完成剩余任务,则恰好与计划工时相等。那么,该任务的计划工时是( ) 小时。A.25
B.22
C.16
D.13答案:C解析:(甲+乙) (t-5)= (甲+乙) *6+乙(t-6), 可得甲:乙=5: (t-11),又因为甲=乙,t=16。 -
第5题:
现由甲、乙、丙三人完成一项工程,如果由甲、乙两人合作,需要12小时完成;如果由乙、丙两人合作,需要l0小时完成;如果甲、乙、丙三人合作,需要6小时才能完成,则这项工程如果全部由甲单独完成,所需小时数为( )。A.15
B.18
C.20
D.25答案:A解析:由题意知,甲、乙、丙三人合作需6小时完成,乙、丙两人合作需10小时完成,则甲单独
{图}
