从一块正方形木板上锯下宽5cm的一个木条后，剩下的长方形面积是750cm2,锯下的木条面积是多少平方厘米？ A. 25 B. 150 C. 152 D. 168

题目
从一块正方形木板上锯下宽5cm的一个木条后，剩下的长方形面积是750cm2,锯下的木条面积是多少平方厘米？

A. 25
B. 150
C. 152
D. 168
相似考题

1.在剧销薄板时可将薄板零件夹在两块木板之间然后按线锯下即可。此题为判断题(对，错)。

2.有四块小场地：第一块是边长a米的正方形，第二块是边长b米的正方形，其余两边都是长a米、宽b米的长方形。另有一块大长方形场地，它的面积等于上面四块场地面积的和，它的长为2(a+b)米，用最简单的式子表示出大长方形的宽

3.一个长方形的长减少5cm，宽增加2cm，就成为一个正方形，并且这两个图形的面积相等。这个长方形的长、宽各是多少

4.一个长方形，若将短边长度增加4厘米，长边长度增加一倍，则面积是原来的3倍，若将长边缩短8厘米，就成正方形，则原长方形面积是多少平方厘米?( )A．180B．128C．84D．48

更多“从一块正方形木板上锯下宽5cm的一个木条后，剩下的长方形面积是750cm2,锯下的木条面积是多少平方厘米？ ”相关问题

  • 第1题：

    用长16厘米的铁丝围成各种长方形(长、宽均为整数，且长和宽不相等)，围成最大的一个长方形面积是多少平方厘米?（ ）

    A．16

    B．15

    C．12

    D．9


    正确答案：B

    设长方形的长为a，宽为b，则这个问题就是求已知a+b=8、且a≠b时，a×b的最大值。为了便于观察，我们分析如下：
    8=1+7→1×7=7；8=2+6→2×6=12；
    8＝3+5→3×5＝15；8—4+4→4×4＝16；
    8＝5+3→5×3＝15；8＝6+2＝6×2＝12；
    8＝7+1＝7×1＝7。
    我们发现当a从小到大取值，而b从大到小取值时，a与b的积呈现这样一个变化趋势：就是先由小到大，再由大到小，中间是最大的，也就是a与b取的数越接近，它们的乘积就越大。当a—b时，a×b的值最大。由此，得出一条规律：
    如果a+b一定，只有当a—b时，a与b的乘积才最大。
    由上面的讨论可知，在a十b＝8，且a≠b中，当a＝3，b＝5时，a×b的最大值是：3×5＝15。
    所以，所围成的最大的一个长方形面积是l5平方厘米。故本题正确答案为B。

  • 第2题：

    一个正方形的一边减少20%，另一边增加2，得到长方形的面积与原正方形的面积相等，问正方形面积是多少?

    A．8

    B．10

    C．16

    D．64


    正确答案：D
    [答案] D。解析：设正方形的边长为x，(1-20%)×(x+2)=x2,x=8。原正方形的面积为64。

  • 第3题：

    用长16厘米的铁丝围成各种长方形（长、宽均为整数，且长和宽不相等），围成的最大的一个长方形的面积是多少平方厘米？（ ）

    A. 16
    B. 15
    C. 12
    D. 9

    答案：B
    解析：
    设长方形的长为a，宽为b，则这个问题就是求已知a+b=8、且a≠b时，axb的最大值。为了便于观察，我们分析如下：
    8 = 1 + 7→1X7=7；8 = 2 + 6→2X6 = 12；
    8 = 3 + 5→3 X5=15；8 = 4 + 4→4 X 4 = 16；
    8 = 5 + 3→5X3=15；8 = 6 + 2 → 6X2 = 12；
    8 = 7 + 1→ 7X1=7。
    我们发现当a从小到大取值，而b从大到小取值时，a与b的积呈现这样一个变化趋势：就是先由小到大，再由大到小，中间是最大的，也就是a与b取的数越接近，它们的乘积就越大。当a = b时，aXb的值最大。由此，得出一条规律：
    如果a+b—定，只有当a =b时，a与b的乘积才最大。
    由上面的讨论可知，在a +b=8，且a≠b中，当a=3，b= 5时，aXb的最大值是：3X5 = 15。 所以，所围成的最大的一个长方形的面积是15平方厘米。故本题正确答案为B。

  • 第4题：

    如下图所示，一张边长8厘米的正方形纸片先进行对折，再沿着两边的中点连线减掉一个角后，则剩下部分展开面积是多少平方厘米？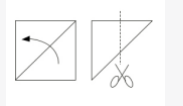

    A.16
    B.32
    C.36
    D.48

    答案：D
    解析：

  • 第5题：

    因木料两头损坏，小明先将-根长12米的木料的两端各锯下1米，然后锯了4次，.锯成等长的短木条，那么，每根短木条长( ) 米。


    A.2.4
    B.2.5
    C.2
    D.2.25

    答案：C
    解析：
    简单计算问题，12米的木材两端各锯下1米，还剩下10米。然后锯4次，分成5根相同长度的木条，每根长度为2米。

  • 第6题：

    一个长方形的长与宽的比是14：5，如果长减少l3厘米，宽增加l3厘米，则面积增加182平方厘米，那么原长方形面积是多少平方厘米?

    A.448
    B.630
    C.812
    D.1120

    答案：B
    解析：
    设原长方形的长为l4a，宽为5a，由题意可得，(14a一l3)x(5a+13)=14a×5a+182，解得a=3，
    原长方形面积是14×3×5×3=630平方厘米，应选择8。

  • 第7题：

    一个工人锯一根22米长的木料，因木料两头损坏，他先将木料两头各锯下1米，然后锯了4次，锯成同样长的短木条，每根短木条长多少米：

    A5.25米
    B5米
    C4.2米
    D4米


    答案：D
    解析：
    木料本来长22米，两头各锯下1米后，还剩20米。在20米的长木中，锯4次，即分成5份，每份长度相等，则每份木料的长度为：20÷5=4米。故正确答案为D。

  • 第8题：

    绝缘站台用干燥的木板或木条制成，木条间距不小于2.5C.m，以免鞋跟陷人。


    正确答案:错误

  • 第9题：

    薄板料的锯削应该尽可能（）。

    • A、分几个方向锯下
    • B、快速的锯下
    • C、缓慢的锯下
    • D、从宽面上锯下

    正确答案:D

  • 第10题：

    用细木条钉成的长方形框，沿对角线拉成一个平行四边形，它的面积（）。

    • A、比原来小
    • B、比原来大
    • C、与原来相等

    正确答案:A

  • 第11题：

    绝缘站台用干燥的木板或木条制成，木条间距不小于2.5mm，以免鞋跟陷入。（）


    正确答案:错误

  • 第12题：

    问答题
    观察一块木板，怎样才能说明它是由树干中央部分锯下来的？

    正确答案： 由树干中央部分锯下的木板上应显示出维管射线的高度和长度，射线应呈砖墙状。
    解析： 暂无解析

  • 第13题：

    从一块正方形木板上锯下宽5cm的一个木条后，剩下的长方形面积是750cm2,锯下的木条面积是多少平方厘米？

    A．25

    B．150

    C．152

    D．168


    正确答案：B
    【答案】B
    【解析】根据题意，此值必能被5整除，排除C、D。A、B值加750，必是平方数，选B。

  • 第14题：

    一个正方形面积是44平方厘米,在这个正方形中作的最大的圆的面积是()平方厘米。

    A.4π

    B.11π

    C.5π

    D.7π


    正确答案：B

  • 第15题：

    如图所示，长方形恰好分为六个正方形，其中最小的正方形面积为1平方厘米，则这个长方形的面积是：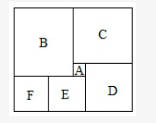

    A.143平方厘米
    B.132平方厘米
    C.110平方厘米
    D.90平方厘米

    答案：A
    解析：
    第一步，本题考查几何问题，属于平面几何类。
    第二步，设正方形E、F的边长为x厘米，则B正方形边长为（2x－1）厘米，D正方形边长为（x＋1）厘米，C正方形边长为（x＋2）厘米。
    第二步，根据宽相等可以建立等式（2x－1）＋x＝（x＋2）＋（x＋1），解得x＝4。
    第三步，宽为（2x－1）＋x＝11（厘米），长为2x－1＋x＋2＝13（厘米）。面积为11×13＝143（平方厘米）。

  • 第16题：

    从一块正方形木板上锯下宽5cm的一个木条后。剩下的长方形面积是750cmz．锯下的木条面积是多少平方厘米?（）
    A.25
    B.150
    C.152
    D.168


    答案：B
    解析：
    根据题意画出下图：

    设正方形的边长为xcm，那么最后剩下的长方形的宽为(x-5)cm，则x(x-5)=750，解得x=30cm，因此锯掉的木条面积为30×5=150c㎡。
    另解，可以直接观察选项，与750的和为完全平方数的即为答案，只有B项满足。

  • 第17题：

    一个箱子的底部由5块正方形纸板 ABCDE和1块长方形纸板F拼接而成（如图所示）,已知A、B两块纸板的面积比是1:16,假设A纸板的边长为2厘米,则该箱子底部的面积为（ ）平方厘米。


    A.200
    B.320
    C.360
    D.420

    答案：C
    解析：
    第一步，本题为几何问题。第二步，A、B面积之比是1:16，则边长之比是1:4，A的边长为2，可知B的边长为8。各线段长度标注在图形上如下：



    第三步，可知整个底部的面积是（10+8）×（8+6+6）=18×20=360。因此，选择C选项。

  • 第18题：

    如图，有大小两个正方形，其对应边的距离均为1厘米。如果两个正方形之间部分的面积是20平方厘米，那么，小正方形的面积是多少平方厘米？（ ）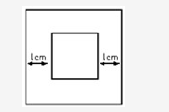


    A4
    B9
    C16
    D25


    答案：C
    解析：
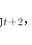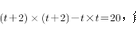    设小正方形的边长为，则大正方形的边长为，依题意有，解之得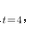，所以面积为16。

    故正确答案为C。

  • 第19题：

    将一块长10厘米、宽4厘米的长方形平板切割成A、B、C共3块，其中C块的面积为22平方厘米，B为等腰三角形，那么A块的面积是（ ）。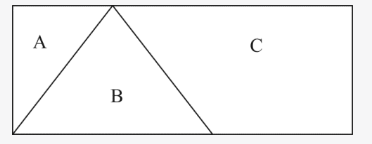

    A.6平方厘米
    B.12平方厘米
    C.8平方厘米
    D.4平方厘米

    答案：A
    解析：
    第一步，本题考查几何问题，属于平面几何的面积计算问题。
    第二步，长方形的长为10厘米，宽为4厘米，那么该矩形的面积为10×4＝40（平方厘米），C的面积为22平方厘米，那么A＋B的面积为40－22＝18（平方厘米）。做三角形B的垂线，如图所示，B为等腰三角形，则三线合一，那么可得三角形A的面积为三角形B的面积的一半，则△B的面积＝2×△A的面积。那么△A的面积为18÷3＝6（平方厘米）。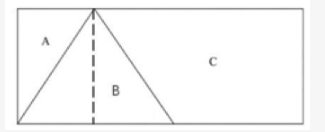

  • 第20题：

    一个工人锯一根22米长的木料，因木料两头损坏，他先将木料两头各锯下1米，然后锯了4次，锯成同样长的短木条，每根短木条长多少米？

    • A、5.25米 
    • B、5米 
    • C、4.2米 
    • D、4米

    正确答案:D

  • 第21题：

    观察一块木板，怎样才能说明它是由树干中央部分锯下来的？


    正确答案: 由树干中央部分锯下的木板上应显示出维管射线的高度和长度，射线应呈砖墙状。

  • 第22题：

    锯割薄板料时，应尽可能（）。

    • A、从宽面上锯下去
    • B、从狭面上锯下去
    • C、把板料夹在两木板之间锯下去
    • D、把板料夹在两块木板之间，连木板一起锯下去

    正确答案:A

  • 第23题：

    单选题
    用细木条钉成的长方形框，沿对角线拉成一个平行四边形，它的面积（）。
    A

    比原来小

    B

    比原来大

    C

    与原来相等


    正确答案： A
    解析： 暂无解析

相关内容