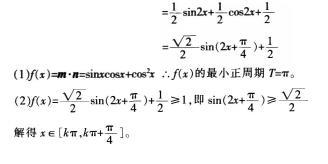高中数学经典50题(附答案)
设R(t)表示可靠度函数，F(t)表示累积故障分布函数，则以下描述正确的是（ ）。
A.R(t)是[0，∞)区间内的非减函数，且0≤R(t)≤1
B.R(t)是[0，∞]区间内的非增函数，且0≤R(t)≤l
C.在(0，∞)区间内，R(t)+F(t)=l
D.F(t)在[0，∞]区间内的非减函数，且0≤F(t)≤1
E.F(t)在[0，∞]区间内的非增函数
可靠度函数R(t)、累积故障分布函数F(t)和故障密度分布函数f(t)三者关系正确的有( )。
A.f(t)+F(t)=1
B.R(t)+F(t)=1
C.R(t)=tfudu
D.F(t)=0f(u)du
设R(t)表示可靠度函数，F(t)表示累积故障分布函数，则下列表述正确的有( )。
A．R(t)是[0，∞)区间内的非减函数，且0≤R(t)≤1
B．R(t)是[0，∞)区间内的非增函数，且0≤R(t)≤1
C．在[0，∞)区间内，R(t)+F(t)=1
D．F(t)在[0，∞)区间内的非减函数，且0≤F(t)≤1
E．F(t)在[0，∞)区间内是非增函数
解析：可靠度R(t)随时间推移越来越低，是[0，∞)区间内的非增函数，且0≤R(t)≤1；而F(t)是[0，∞)区间内的非减函数，且0≤F(t)≤1；在[0，∞)区间内，R(t)+F(t)=1。
A. 2X(t)
B. X(t )
C. X(f)
D. 2X(f)
摘要:高中数学经典50题(附答案)高中数学题库1.求下列函数的值域：解法2令t＝sinx，则f(t)＝－t2＋t＋1，∵|sinx|≤1,∴|t|≤1.问题转化为求关于t的二次函数f(t)在闭区间[－1,1]上的最值．本例题(2)解法2通过换元，将求三角函数的最值问题转化为求二次函数在闭区间上的最值问题，从而达到解决问题的目的，这就是转换的思想．善于从不同角度去观察问题，沟通数学各学科之间的内在联系，是实现转换的关键，转换的目的是将数学问题由陌生化熟悉由复杂化简单，一句话：由难化易．可见化归是转换的目的，而转换是实现化归段手段。2.设有一颗慧星沿一椭圆轨道绕地球运行，地球恰好位于椭圆轨道的焦点处，当此慧星离地球相距为万千米和万千米时，经过地球和慧星的直线与椭圆的长轴夹角分别，求该慧星与地球的最近距离。解：建立如下图所示直角坐标系，设地球位于焦点1/52处，椭圆的方程为 高中数学经典50题(附答案)（图见教材P132页例1）。当过地球和彗星的直线与椭圆的长轴夹角为能满足时，由椭圆的几何意义可知，彗星A只。作故由椭圆第二定义可知得两式相减得答：彗星与地球的最近距离为万千米。说明：（1）在天体运行中，彗星绕恒星运行的轨道一般都是椭圆，而恒星正是它的一个焦点，该椭圆的两个焦点，一个是近地点，另一个则是远地点，这两点到恒星的距离一个是，另一个是（2）以上给出的解答是建立在椭圆的概念和几何意义之上的，以数学概念为根基充分体现了数形结合的思想。另外，数学应用问题的解决在数学化的过程中也要时刻不忘审题，善于挖掘隐含条件，有意识地训练数学思维的品质。3.A，B，C是我方三个炮兵
求下列象函数的原函数f(t)。
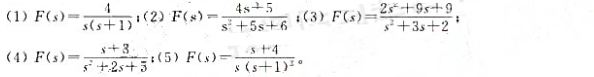
设R(t)表示可靠度函数，F(t)表示累积故障分布函数，则以下表述正确的是( )。
A．R(t)是[0，∞)区间内的非减函数，且0≤R(t)≤1
B．R(t)是[0，∞]区间内的非增函数，且0≤R(t)≤1
C．在(0，∞)区间内，R(t)+F(t)＝1
D．F(t)在[0，∞]区间内的非减函数，且0≤F(t)≤1
E．F(t)在[0，∞]区间内是非增函数
A.R(t)是[0,∞)区间内的非减函数，且0≤R(t)≤1
B.R(t)是[0, ∞)区间内的非增函数，且0≤R(t)≤1
C.在[0,∞)区间内，R(t) +F(t) =1
D. F(t)在[0,∞)区间内的非减函数，且0≤F(t)≤1
E.F(t)在[0,∞)区间内是非增函数
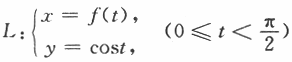，其中函数f(t)具有连续导数，且f(0)=0，f'(t)>0(0
(1)求函数f(x)的最小正周期：
(2)若f(x)≥1，求f(x)的取值范围。
