常微分课后答案第五章20220728.doc
此题为判断题(对,错)。
非齐次线性方程组任意两个解之差为对应系数的齐次线性方程组的解。()
 是线性方程组
是线性方程组 的解,
的解, 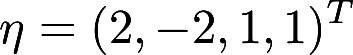 是它的导出组的解,求方程组的通解。
是它的导出组的解,求方程组的通解。
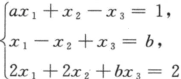 的解的情况,在方程组有解时求出其解,其中a,b为常数.
的解的情况,在方程组有解时求出其解,其中a,b为常数.
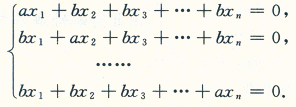
其中a≠0,b≠0,n≥2.试讨论a,b为何值时,方程组仅有零解,有无穷多组解?在有无穷多组解时,求出全部解,并用基础解系表示全部解.

. . 28/28第五章 线性微分方程组5.1 存在唯一性定理习题5.1 1给定方程组, (*)试验证,分别是方程组(*)的满足初始条件,的解;试验证是方程组(*)的满足初始条件的解,其中是任意常数证明,显然,所以,分别是方程组(*)的满足初始条件,的解,又,所以是方程组(*)的满足初始条件的解,其中是任意常数2将下面的初值问题化为与之等价的一阶方程组的初值问题:,;,;, (提示:令)解设,则,即与该初值问题等价的一阶方程组的初值问题为设,则,则得等价的一阶方程组的初值问题为,令,有 ,为与原初值问题等价的一阶方程组的初值问题3试用逐步逼近法求方程组, 满足初始条件的第三次近似解解,第三次近似解为 5.2 线性微分方程组的一般理论习题5.2 1试验证是方程组,在任何不包含原点的区间上的基解矩阵证明设,则由于,所以都是方程组的解,因而是所给方程组的解矩阵又由于在任何不包含原点的区间上,(),故是所给方程组的基解矩阵2考虑方程组, (5.15)其中是区间上的连续矩阵,它的元素为,如果是(5.15)的任意个解,那么它们的Wronsky行列式满足下面的一阶线性微分方程(提示:利用行列式的微分公式,求出的表达式);解上面的一阶线性微分方程,证明下面的公式:,证明,所以是一阶线性微分方程的解由知,分离变量后两边积分求解得,时就得到,所以,3设为区间上的连续实矩阵,为方程的基解矩阵,而为其一解试证:对于方程的任一解必有常数;为方程的基解矩阵的充要条件是存在非奇异的常数矩阵,使证明由于是方程的解,故有,为方程的解,故所以,所以常数“”是方程的基解矩阵,因此,是方程的基解矩阵,故,且和所以,故是常数矩阵,设,则,因此存在非奇异常数矩阵,使“”若存在非奇异常数矩阵,使,则有,所以,即是非奇异矩阵或说的各列是线性无关的又,并注意到,有,即从而是方程的基解矩阵4设为方程(为常数矩阵)的标准基解矩阵(即),证明,其中为某一值证明 由于为常数矩阵,故在有定义、连续,从而它的解也在连续可导由为方程的基解矩阵,故,有,并且有,从而对某个,有,且,即亦为方程的基解矩阵由推论2*,存在一个非奇异常数矩阵,使得在区间上,又因为,所以因此,其中为某一值5设分别为在区间上连续的矩阵和维列向量证明方程组存在且最多存在个线性无关解证明 设方程组的基解矩阵为,而是方程组的一个特解,则其通解为,其中是任意的常数列向量若不恒为0,则必与线性无关,从而,线性无关,即方程组存在个线性无关解又假若是方程组的任意一个解,则一定有确定的常数列向量,使得,将其加入,这一组向量就线性相关,故方程组的任何个解必线性相关从而方程组存在且最多存在个线性无关解6试证非齐线性微分方程组的叠加原理:设分别是方程组,的解,则是方程组的解证明 因为分别是方程组,的解,故,所以有,所以是方程组的解7考虑方程组,其中,试验证是的基解矩阵;试求的满足初始条件的解证明,成立而,所以是的基解矩阵,这样,由定理8,方程组满足初始条件的解就是,对应的齐线性方程组满足初始条件的解就是,所以,所求方程组的满足初始条件的解为8试求,其中,满足初始条件的解解 由上题知,且这里,所以,所求方程组的满足初始条件的解为9试求下列方程的通解:,;解易知对应的齐线性方程的基本解组为,用公式(5.31)来求方程的一个解这时,取,有所以方程的通解为 由于特征方程的根是,故对应的齐线性方程的基本解组为,原方程的一个特解由公式(5.29)有(取),其中,所以,故通解特征方程,得到特征根,故对应的齐线性方程的基本解组为,取,由(5.31),得特解,所以得到通解10给定方程,其中在上连续,试利用常数变易公式,证明:若在上有界,则上面方程的每一个解在上有界;若当时,则上面方程的每一个解,满足(当时)证明 对应的特征方程有特征根,故对应的齐线性方程的基本解组,由公式(5.31)得原方程的一个特解()为,所以方程的任一解可写为由于在上有界,故,有又由于,从而当时,即方程的每一个解在上有界当时,故由知,若有界,则,若无界,由于在连续,故为无穷大量,因此,即总有同理从而对方程的每一个解,有11给定方程组,这里是区间上的连续矩阵设是它的一个基解矩阵,维向量函数在上连续,试证明初值问题: (*)的唯一解是积分方程组 (*)的连续解反之,(*)的连续解也是初值问题(*)
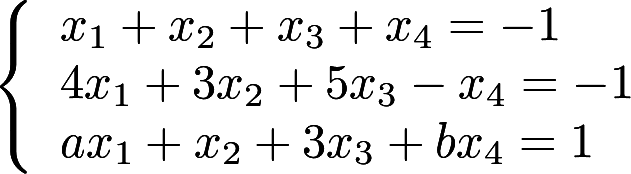 有3个线性无关的解. (Ⅰ)证明方程组系数矩阵A的秩
有3个线性无关的解. (Ⅰ)证明方程组系数矩阵A的秩 ; (Ⅱ)求
; (Ⅱ)求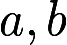 的值及方程组的通解
的值及方程组的通解

 是线性方程组
是线性方程组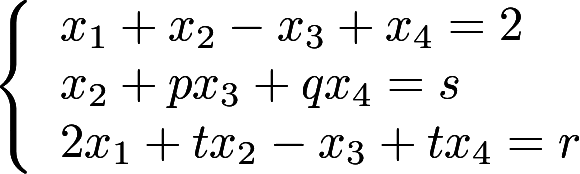 的解,
的解, 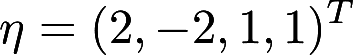 是它的导出组的解,求方程组的通解。
是它的导出组的解,求方程组的通解。

其中a≠0,b≠0,n≥2.试讨论a,b为何值时,方程组仅有零解,有无穷多组解?在有无穷多组解时,求出全部解,并用基础解系表示全部解.

 有3个线性无关的解. (Ⅰ)证明方程组系数矩阵A的秩
有3个线性无关的解. (Ⅰ)证明方程组系数矩阵A的秩 ; (Ⅱ)求
; (Ⅱ)求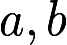 的值及方程组的通解
的值及方程组的通解

 的解的情况,在方程组有解时求出其解,其中a,b为常数.
的解的情况,在方程组有解时求出其解,其中a,b为常数.
更多 “常微分课后答案第五章20220728.doc” 相关考题
相关内容
最新试卷
热门试卷
- 2022年高考真题——地理(广东卷) Word版-
- 2022年高考真题——历史(广东卷) Word版含解析(部分试题)-
- 2022年高考真题——理综生物(全国乙卷) Word版含解析-
- 2022年高考真题——语文(浙江卷) Word版含解析-
- 2022年高考真题——理综化学(全国乙卷) Word版含解析-
- 2022年高考真题——物理(广东卷) Word版含解析-
- 2022年高考真题——化学(全国甲卷) Word版含解析-
- 2022年高考真题——文综地理(全国乙卷) Word版含解析-
- 2022年高考真题——化学(广东卷) Word版含解析-
- 2022年高考真题——通用技术(浙江卷) Word版含解析-
