单选题采用对流换热边界层微分方程组，积分方程组或雷诺类比法求解对流换热过程中，正确的说法是（ ）。A 微分方程组的解是精确解B 积分方程组的解是精确解C 雷诺类比的解是精确解D 以上三种均为近似值

题目
单选题
采用对流换热边界层微分方程组，积分方程组或雷诺类比法求解对流换热过程中，正确的说法是（  ）。
A

微分方程组的解是精确解

B

积分方程组的解是精确解

C

雷诺类比的解是精确解

D

以上三种均为近似值

相似考题

1.设线性方程组AX=b有唯一解,则相应的齐次方程组AX=0解的情况是()。A.有非零解B.只有零解C.无解D.解不能确定

2.非齐次线性方程组任意两个解之差为对应系数的齐次线性方程组的解。()

3.牛顿－拉夫逊迭代法的基本原理是用泰勒级数展开非线性方程组,略去二阶及以上的高阶项得到线性修正方程组,通过一次求解修正方程组和修正未知量就可得到未知量的精确解。()此题为判断题(对，错)。

4.齐次线性方程组任意两个解之线性组合仍然是原方程组的解。()此题为判断题(对，错)。

更多“单选题采用对流换热边界层微分方程组，积分方程组或雷诺类比法求解对流换热过程中，正确的说法是（ ）。A 微分方程组的解是精确解B 积分方程组的解是精确解C 雷诺类比的解是精确解D 以上三种均为近似值”相关问题

  • 第1题：

    讨论方程组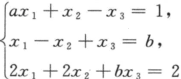的解的情况,在方程组有解时求出其解,其中a,b为常数.


    答案：
    解析：

  • 第2题：

    已知下列非齐次线性方程组(Ⅰ)，(Ⅱ)
    　　
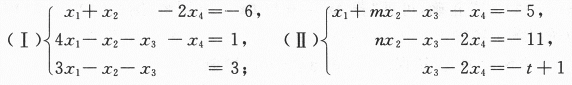
    　　(1)求解方程组(Ⅰ)，用其导出组的基础解系表示通解.
    　　(2)当方程组中的参数m，n，t为何值时，方程组(Ⅰ)与(Ⅱ)同解.


    答案：
    解析：

  • 第3题：

    采用对流换热边界层微分方程组、积分方程组或雷诺类比法求解，对流换热过程中，正确的说法是（　　）。

    A． 微分方程组的解是精确解
    B． 积分方程组的解是精确解
    C． 雷诺类比的解是精确解
    D． 以上三种均为近似解

    答案：A
    解析：
    对流换热的求解方法包括分析法、类比法和实验法。分析法包括微分方程组求解和积分方程组求解。在所有方法中，只有微分方程组的解是精确解；积分方程组的求解要先假设速度和温度的分布，因此是近似解；雷诺类比的解是由比拟理论求得的，也是近似解。

  • 第4题：

    已知方程组(I)(II)图1} (1)a,b取什么值时这两个方程组同解?此时求解. (2)a,b取什么值时这两个方程组有公共解? 此时求公共解{


    答案：
    解析：

  • 第5题：

    已知齐次线性方程组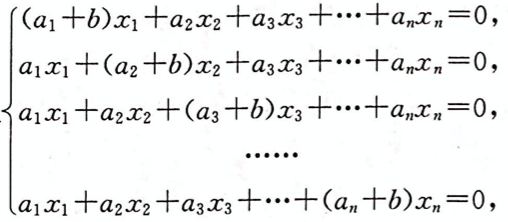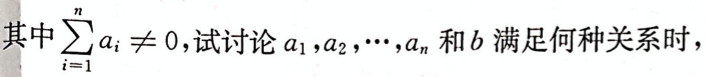（1）方程组仅有零解；（2）方程组有非零解，在有非零解时，求此方程组的一个基础解系.


    答案：
    解析：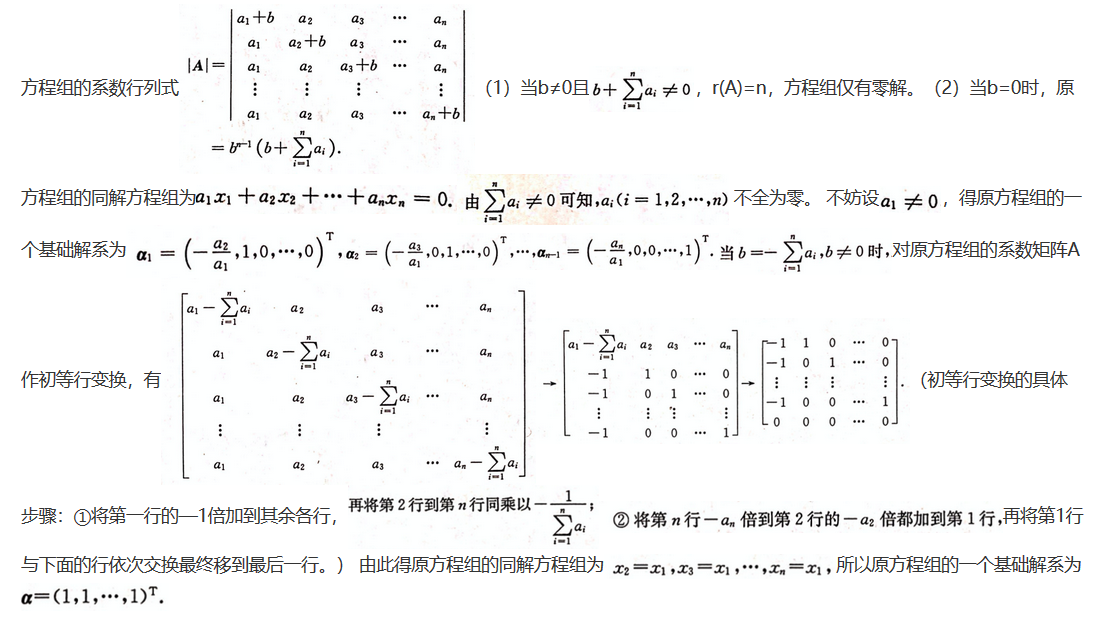

  • 第6题：

    设线性方程组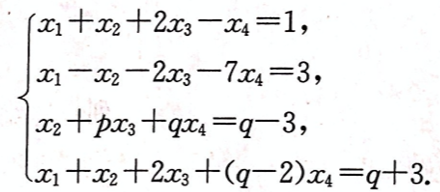问方程组何时无解，有唯一解，有无穷多解，有无穷多解时，求出其全部解。


    答案：
    解析：
    将方程组的增广矩阵作初等行变换，有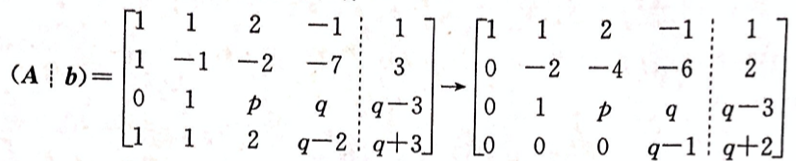

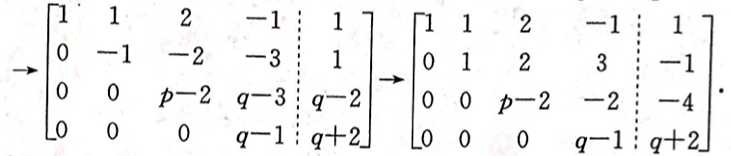
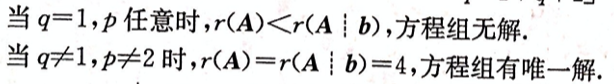
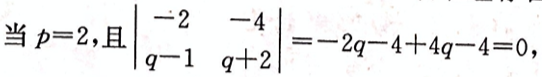
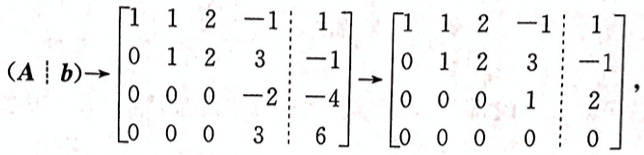
  • 第7题：

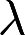    取何值时,非齐次线性方程组 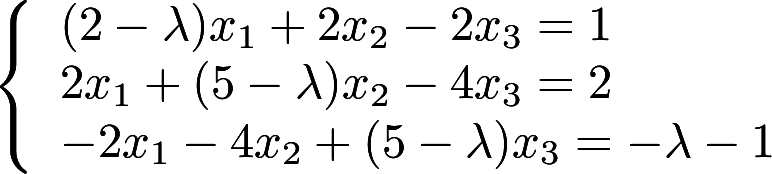(1)有唯一解 (2)无解 (3)有无穷多个解? 并在无穷多个解时，求方程组的通解。


    答案：
    解析：

  • 第8题：

    设A是m×n阶矩阵,下列命题正确的是().

    A.若方程组AX=0只有零解,则方程组AX=b有唯一解
    B.若方程组AX=0有非零解,则方程组AX=b有无穷多个解
    C.若方程组AX=b无解,则方程组AX=0一定有非零解
    D.若方程组AX=b有无穷多个解,则方程组AX=0一定有非零解

    答案：D
    解析：

  • 第9题：

    下列关于边界层流动的说法正确的是（）

    • A、在边界层内，沿物体表面的法线方向压强是可变的
    • B、布拉休斯解是精确解
    • C、动量积分关系式方法的解是精确解
    • D、摩擦阻力系数与雷诺数成反比

    正确答案:B

  • 第10题：

    单选题
    下列关于边界层流动的说法正确的是（）
    A

    在边界层内，沿物体表面的法线方向压强是可变的

    B

    布拉休斯解是精确解

    C

    动量积分关系式方法的解是精确解

    D

    摩擦阻力系数与雷诺数成反比


    正确答案： D
    解析： 暂无解析

  • 第11题：

    单选题
    采用对流换热边界层微分方程组，积分方程组或雷诺类比法求解对流换热过程中，正确的说法是（　　）。[2010年真题]
    A

    微分方程组的解是精确解

    B

    积分方程组的解是精确解

    C

    雷诺类比的解是精确解

    D

    以上三种均为近似值


    正确答案： C
    解析：
    对流换热的求解方法包括分析法、类比法和实验法。分析法包括微分方程组求解和积分方程组求解。在所有方法中，只有微分方程组的解是精确解；积分方程组的求解要先假设速度和温度的分布，因此是近似解；雷诺类比的解是由比拟理论求得的，也是近似解。

  • 第12题：

    问答题
    说明对流换热微分方程组由哪几个方程组成？它们各自导出的理论依据是什么？

    正确答案： 对流换热的微分方程组包括：连续性方程，动量微分方程，能量微分方程。
    导出的理论依据：
    1.连续性方程：根据微元体的质量守恒导出；
    2.动量微分方程：根据微元体的动量守恒导出；
    3.能量微分方程，根据微元体的质量守恒导出。
    解析： 暂无解析

  • 第13题：

    设齐次线性方程组
    　　
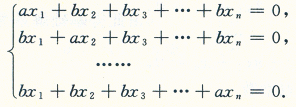
    　　其中a≠0，b≠0，n≥2.试讨论a，b为何值时，方程组仅有零解，有无穷多组解？在有无穷多组解时，求出全部解，并用基础解系表示全部解.


    答案：
    解析：

  • 第14题：

    采用对流换热边界层微分方程组，积分方程组或雷诺类比法求解对流换热过程中，正确的说法是( )。

    A.微分方程组的解是精确解
    B.积分方程组的解是精确解
    C.雷诺类比的解是精确解
    D.以上三种均为近似值

    答案：A
    解析：
    对流换热的求解方法大纲要求知道三种：分析法、类比法和实验法。分析法包括微分方程组求解和积分方程组求解。所有方法中，只有微分方程组的解是精确解，其他方法都是近似值。

  • 第15题：

    对于常规的技术方案，在采用直线内插法近似求解财务内部收益率时，近似解与精确解之间存在的关系是( )。

    A、近似解＜精确解
    B、近似解>精确解
    C、近似解=精确解
    D、不确定关系

    答案：B
    解析：
    2020/2019版教材P25
    图1Z10I026 常规技术方案的净现值函数曲线，理解透彻，看清楚，财务净现值呈下凹状，

  • 第16题：

    问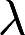取何值时 非齐次线性方程组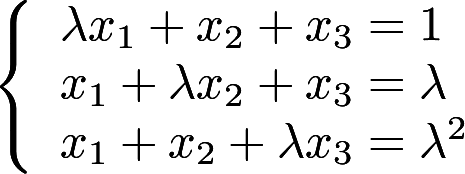， (1)有唯一解 (2)无解 (3)有无穷多个解，并在无穷多个解时，求方程组的通解


    答案：
    解析：

  • 第17题：

    已知是线性方程组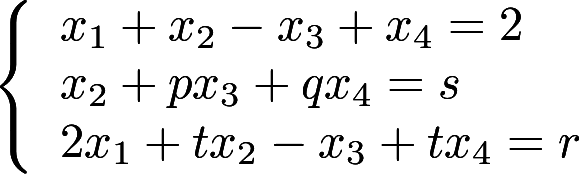的解, 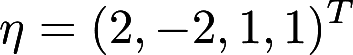是它的导出组的解,求方程组的通解。


    答案：
    解析：

  • 第18题：

    当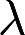取何值时,方程组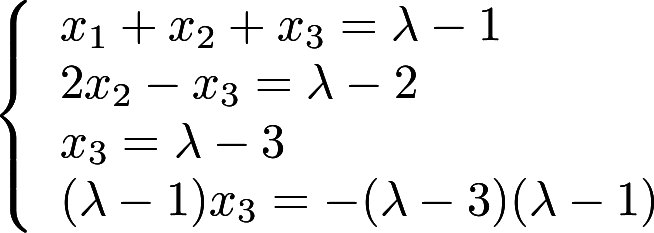有唯一解，并求解。


    答案：
    解析：

  • 第19题：

    设A是m×N阶矩阵,B是n×m阶矩阵,则().


    A.当m>n时,线性齐次方程组ABX=0有非零解
    B.当m>n时,线性齐次方程组ABX=0只有零解
    C.当n>m时,线性齐次方程组ABX=0有非零解
    D.当n>m时,线性齐次方程组ABX=0只有零解


    答案：A
    解析：
    AB为m阶方阵，当m>n时，因为r(A)≤n，r(B)≤n且r(AB)≤min{r(A)，r(B)}，所以r(AB)

  • 第20题：

    设α是某一方程组的解向量，k为某一常数，则kα也为该方程组的解向量。（　　）


    答案：错
    解析：

  • 第21题：

    紫外－可见分光光度法中多组分定量方法中，如果两组分吸收曲线重叠时候可以采用（）定量。

    • A、解二元一次联立方程组
    • B、解二元二次联立方程组
    • C、解一元二次联立方程组
    • D、解二元三次联立方程组

    正确答案:A

  • 第22题：

    问答题
    设AX=0与BX=0均为n元齐次线性方程组，秩r（A）=r（B），且方程组AX=0的解均为方程组BX=0的解，证明方程组AX=0与BX=0同解.

    正确答案：
    设r(A)=r(B)=r,方程组AX=0的基础解系为①:ζ1,ζ2,…,ζn-r,方程组BX=0的基础解系为②:η1,η2,…,ηn-r.
    构造向量组③:ζ1,ζ2,…,ζn-r,η1,η2,…,ηn-r.
    由向量组①可由②线性表示,则向量组②和③等价,从而r(③)=n-r,所以ζ1,ζ2,…,ζn-r是向量组③的极大线性无关组,有η1,η2,…,ηn-r可由ζ1,ζ2,…,ζn-r线性表示,即BX=0的任一解都可由ζ1,ζ2,…,ζn-r线性表示,故BX=0的解都是AX=0的解,所以方程组AX=0与BX=0同解.
    解析： 暂无解析

  • 第23题：

    单选题
    对于常规的技术方案，在采用直线内插法近似求解财务内部收益率时，近似解与精确解之间存在的关系是（）
    A

    近似解<精确解

    B

    近似解>精确解

    C

    近似解-精确解

    D

    不确定关系


    正确答案： B
    解析： 暂无解析

相关内容