2022年福建省永春一中高二数学竞赛班讲义递推数列求通项含参考答案
数列是高中数学很重要的内容之一,数列中求通项的问题也是最常见的题型,其形式多样,解法灵活。请谈谈你认为的几种常用的求数列通项的方法。
纲要:举例说明,有:迭加法,迭乘法,换元法,倒数法,待定系数法,分类讨论等等(需简要说明每种方法适用的情况)。
以下算法设计基本方法中基本思想不属于归纳法的是( )
A.递推法
B.递归法
C.减半递推技术
D.回溯法
已知数列{an}的前n项和Sn=n2-2n.求
(I){an}的前三项;
(II){an}的通项公式.
常用于解决“是否存在”或“有多少种可能”等类型的问题(例如求解不定方程的问题)的算法设计基本方法是( )
A.归纳法
B.递推法
C.列举法
D.减半递推技术
A.逐步求精
B.实验法
C.原型法
D.递推法
答案:C
2022年永春一中高二数学竞赛班讲义第1讲 递推数列求通项班级 姓名 一、知识要点:1累加法,累乘法,待定系数法,取倒数法,取对数法,数学归纳法,与转化法。较难的求通项方法:1除法:由形如的递推式求通项,可两边同除以转化为形如的递推式。2不动点法:形如的分式递推式:记特征函数的不动点为,当时,成等差数列;当时,成等比数列。3特征根法:在给出的递推式中,记特征方程的两根为,当时,;当时,。4换元法(根号换元,三角换元)5双数列递推、周期数列等。二、例题精析例1(1)已知数列满足,求。(2)已知,求。(3)已知数列中,求。(4)已知,求。(5)已知,求。例2(1)已知数列满足:,求通项。(2)已知数列满足:,求通项。例3(1)已知数列满足:,求通项。(2)已知数列满足:,求通项。例4(1)数列中,求数列的通项公式。(2)数列中,求数列的通项公式。例5(1)数列中,试求(2)设,求并证明。例6数列中,数列中,。当时,求和。三、精选习题1已知数列满足,则 2数列中,则通项 。3已知数列满足,则= 4已知数列中,你有多少种方法求?5已知数列满足:,求通项。6数列满足,求数列的通项公式。7已知数列满足,其中是给定的正实数,求此数列的通项。8已知数列满足:R且,N(1)求数列的通项公式;(2)若,试比较与的大小(2011年高中联赛)高二数学竞赛讲义 数列和与通项 1 参考答案一、例题分析例2(1)设,为常数,用待定系数法求得,所以,故成等比数列,所以。(2)两边同除以,累加得 例3(1)解:令,得,则是函数的两个不动点。因为。所以数列是以为首项,以为公比的等比数列,故,则。(2)解:令,得,则是函数的不动点。因为,所以。例4(1)解:由特征方程,得,所以数列成等比数列,首项为,公比为,则,两边同除以,则,所以数列成等差数列,首项为,公比为,所以,。(2)简例应用(特征根法):数列:, 的特征方程是:,。又由,于是故例5设,则,所以,则,因为,即,则,得,所以(2)由,可知设,则,所以,则,因为当时,所以,证毕。例6解:因所以即(1)又因为所以.即(2)由(1)、(2)得:, 三、巩固练习2 提示:在的两边取常用对数,则,所以数列成等比数列,首项为,公比为,所以,所以3在的两边同除以,则,所以数列成等差数列,首项为,公差为,所以,4法1: , 得,所以数列的奇数项成等差数列,偶数项也成等差数列,所以, ,法2:设,则,所以。故,所以成等比数列,首项,公比是,所以法3:由得,两边同除以累加(右边是错位相减法)求得。6或,则,所以数列是等比数列,公比为,首项为, 特征根法:,或,设,由待定系数,得,所以7令,易求88设,且对所有正整数,有,求能使被 整除的一切的值。8,所以,累加得当或时,能使被 整除8
阅读以下说明和流程图,回答问题将解答填入对应栏内。
[说明]
已知递推数列:a(1)=1,a (2s)= a (s),a(2s+1)=a (s)+a (s+1)(s 为正整数)。试求该数列的第n项与前n项中哪些项最大?最大值为多少?
算法分析:该数列序号分为奇数或偶数两种情况做不同递推,所得数列呈大小有规律的摆动。设置a数组,赋初值a (1)=1。根据递推式,在循环中分项序号s (2~n)为奇数或偶数作不同递推:每得一项 a (s),即与最大值max 作比较,如果a (s)>max,则max=a(i)。最后,在所有项中搜索最大项(因最大项可能多于一项),并打印最大值max。
[问题]
将流程图中的(1)~(5)处补充完整。
注:流程图中(1)循环开始的说明按照“循环变量名:循环初值,循环终值,增量”格式描述。
[流程图]
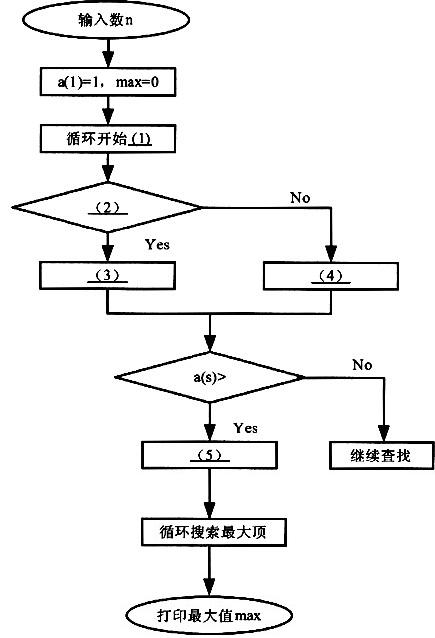
(1)for s=2 to n (2) mod(s,2)=0 (3) a(s)=a(s/2) (4) a(s)=a(s+1)/2+a(s-1)/2) (5) max=a(s)
常用的算法设计方法有:( ) Ⅰ.列举法 Ⅱ.归纳法 Ⅲ.递推 Ⅳ.递归. Ⅴ.回溯法
A.Ⅰ,Ⅱ,Ⅲ,Ⅴ
B.Ⅲ,Ⅳ,Ⅴ
C.Ⅰ,Ⅱ,Ⅴ
D.全是
解析:常用的算法设计方法有:①列举法,就是根据提出的问题,列举所有可能的情况,并用问题中给定的条件检验哪些是需要的,哪些是不需要的。②归纳法,通过列举少量的特殊情况,经过分析,最后找出一般的关系。⑧递推,从已知的初始条件出发,逐次推出所要求的各中间结果和最后结果。④递归,将一个复杂的问题归纳为若干个较简单的问题,然后将这些较简单的每一个问题再归结为更简单的问题,这个过程可以一直做下去,直到最简单的问题为止。⑤减半递推技术,“减半”是指将问题的规模减半,而问题的性质不变,“递归”是指重复“减半”的过程。⑥回溯法,有些实际问题却很难归纳出一组简单的递推公式或直观的求解步骤,并且也不能进行无限的列举。对于这类问题,一种有效的方法是“试”。通过对问题的分析,找出一个解决问题的线索,然后沿着这个线索逐步试探,对于每一步的试探,若试探成功,就得到问题的解,若试探失败,就逐步回退,换别的路线再进行试探。这种方法称为回溯法。
常用的算法设计方法有:( ) Ⅰ.列举法 Ⅱ.归纳法 Ⅲ.递推 Ⅳ.递归 Ⅴ.回溯法
A.Ⅰ,Ⅱ,Ⅲ,Ⅴ
B.Ⅲ,Ⅳ,Ⅴ
C.Ⅰ,Ⅱ,Ⅴ
D.全是
解析:常用的算法设计方法有:①列举法,就是根据提出的问题,列举所有可能的情况,并用问题中给定的条件检验哪些是需要的,哪些是不需要的。②归纳法,通过列举少量的特殊情况,经过分析,最后找出一般的关系。③递推,从已知的初始条件出发,逐次推出所要求的各中间结果和最后结果。④递归,将一个复杂的问题归纳为若干个较简单的问题,然后将这些较简单的每一个问题再归结为更简单的问题,这个过程可以一直做下去,直到最简单的问题为止。⑤减半递推技术,“减半”是指将问题的规模减半,而问题的性质不变,“递归”是指重复“减半”的过程。⑥回溯法,有些实际问题却很难归纳出一组简单的递推公式或直观的求解步骤,并且也不能进行无限的列举。对于这类问题,一种有效的方法是“试”。通过对问题的分析,找出一个解决问题的线索,然后沿着这个线索逐步试探,对于每一步的试探,若试探成功,就得到问题的解,若试探失败,就逐步回退,换别的路线再进行试探。这种方法称为回溯法。
(I)求{an}的通项公式;
(II)求{an)的前5项和.

(Ⅰ)求{an}的通项公式;
(Ⅱ)求{an}的前5项和.

