福建师范大学22春《复变函数》在线作业三及答案参考64

在缓和曲线的始点,缓和曲线倾角和曲率分别为()。

A、1/R，0

B、0，1/R

C、0，0

D、1/R，1/R

参考答案：C

曲线y=e-x在点(0，1)处的切线斜率k=______．

答案：

解析：

求曲线y=e-2x在点M(0，1)处的法线方程．

答案：

解析：

曲线y=ex+x2在点(0，1)处的切线斜率为______．

答案：

解析：

曲线y=x+ex在点(0，1)处的切线斜率k=______．

答案：

解析：

填2．因为y'=1+ex，所以k=y'(0)=2．

福建师范大学22春复变函数在线作业三及答案参考1. 计算曲线y=cosh x上点(0，1)处的曲率.高等数学复旦大学出版第三版上册课后答案习题二计算曲线y=coshx上点(0，1)处的曲率.计算曲线y=cosh x上点(0，1)处的曲率.答案仅供参考，不要直接抄袭哦2. 复合函数y=sin2(2x+5)是由哪些简单函数复合而成的?复合函数y=sin2(2x+5)是由哪些简单函数复合而成的?函数是由y=u2，u=sinv，v=2x+5复合而成的3. 设m=m1m2,且(m1,m2)=1,则(m)等于什么?A、(m1)B、(m2)(m1)C、(m1)*(m1)D、(m2)*(m2)设m=m1m2,且(m1,m2)=1,则(m)等于什么?A、(m1)B、(m2)(m1)C、(m1)*(m1)D、(m2)*(m2)正确答案： B4. ，其中D是由直线x=0，y=和y=x所围成的区域，其中D是由直线x=0，y=和y=x所围成的区域积分区域D如图8.24所示，0y，0xy 5. 使用最小平方法配合趋势直线时，求解a、b参数值的那两个标准方程式为_。使用最小平方法配合趋势直线时，求解a、b参数值的那两个标准方程式为_。y=na+bt ty=at+bt2 6. 一曲边梯形由曲线y=2x2+3，x轴及x=-1，x=2所围成，试列出用定积分表示该曲边梯形的面积表达式一曲边梯形由曲线y=2x2+3，x轴及x=-1，x=2所围成，试列出用定积分表示该曲边梯形的面积表达式S=-12(2x2+3)dx7. 甲、乙两人对策。甲手中有3张牌：2张K，1张A。甲任意藏起一张后然后宣称自己手中的牌是KK或KA，对此乙可以接受或甲、乙两人对策。甲手中有3张牌：2张K，1张A。甲任意藏起一张后然后宣称自己手中的牌是KK或KA，对此乙可以接受或提出异议。如甲叫的正确乙接受，甲得1元；如甲手中是KK叫KA时乙接受，甲得2元；甲手中是KA叫KK时乙接受，甲输2元。如乙对甲的宣称提出异议，输赢和上述恰相反而且钱数加倍。列出甲、乙各自的纯策略，求最优解和对策值，说明对策是否公平合理？游戏公平合理。8. 若fL(X)，则( )A.f在X上几乎处处连续B.存在gL(X)使得|f|=gC.若Xfdu=0，则f=0，a.e.参考答案：B9. 过半径为R的圆周上一点0任意作圆的弦0A，0A与直径0B的夹角X服从均匀分布。求所有这些弦长AB的平均长度及弦长A过半径为R的圆周上一点0任意作圆的弦0A，0A与直径0B的夹角X服从均匀分布。求所有这些弦长AB的平均长度及弦长AB的方差设弦长AB=Y，则Y=2R|sinX|，由于，所以X的概率密度为，由函数的期望公式求得；EY2=2R2；10. 求通过坐标原点，与曲面x2-2yz-2y+4z-3=0相切而且与直线相交的直线方程求通过坐标原点，与曲面x2-2yz-2y+4z-3=0相切而且与直线相交的直线方程设所求直线方程为因为所求直线与相交，所以即X-Y+Z=0且X:Y:Z2:1:(-1)，令，则有 x=tX,y=tY,z=tZ,代入曲面方程得 (tX)2-2t2YZ+2tY+4tZ-3=0, 即(X2-2YZ)t2-(2Y-4Z)t-3=0，因为直线与曲面相切，所以 (2Y-42)2+12(X2-2YZ)=0, 即Y2-4YZ+4Z2+3X2-6YZ=0, 由得X=Y-Z, 代入得Y2-10YZ+4Z2+3(Y-Z)2=0，即4Y2-16YZ+7Z2=0，即(2Y-7Z)(2Y-Z)=0, 所以2Y=7Z或2Y=Z，当2Y=7Z时，当2Y=Z时，所以求得X:Y:2=5:7:2或X:Y:Z=(-1):1:2，故所求直线方程为与 11. 设函数f(x)在(-，+)内有定义，下列函数中必为偶函数的有( ) Ay=|f(x)| By=f(x2) Cy=f(x)+f(-x) D设函数f(x)在(-，+)内有定义，下列函数中必为偶函数的有()Ay=|f(x)|By=f(x2)Cy=f(x)+f(-x)Dy=cBCD解选项A不对，例如f(x)=1+x12. 试证明：设fn(x是R1上非负渐降连续函数列若在有界闭集F上fn(x)0(n)，则fn(x)在F上一致收敛于零试证明：设fn(x是R1上非负渐降连续函数列若在有界闭集F上fn(x)0(n)，则fn(x)在F上一致收敛于零证明由题设可知，对任意的xF以及0，存在自然数指标n，使得fn(x)因为f(x)是连续函数，所以存在x0，使得fn(t)(tB(x，x)注意到B(x，x)是F的开覆盖，故存在有限个开球 B(xi，xi) (i=1，2，m)，记与xi相应的自然数指标为ni(i=1，2，m)，则令N=maxn1，n2，nm，我们得到 fn(x) (nN，xF) 这说明fn(x)在F上一致收敛于0 13. 设星形线x=acos3t，y=asin3t上每一点处的线密度的大小等于该点到原点距离的立方，在原点O处有一单位质点，求星设星形线x=acos3t，y=asin3t上每一点处的线密度的大小等于该点到原点距离的立方，在原点O处有一单位质点，求星形线在第一象限的弧段对这质点的引力14. 设随机变量X的分布律为 X 0 p 0.4 r 0.1设随机变量X的分布律为X0p0.4r0.1且E(X)=0，D(X)=2，试求待定系数，r，其中由离散型随机变量分布律的性质得1=0.4+r+0.1r=0.5 又由数学期望与方差的定义得 E(X)=0=0.4+00.5+0.10.4+0.1=0=-4， D(X)=2=0.4(-0)2+0.5(0-0)2+0.1(-0)20.42+0.12=2，解得=1，=4 又，故=-1，=4，r=0.5小结随机变量的分布律(或概率密度)的性质、数学期望和方差的定义在确定待定系数的题目中经常用到，要灵活掌握三者之间的相互转化关系 15. 若矩阵A可逆，则(2A)-1=2A-1( )若矩阵A可逆，则(2A)-1=2A-1()参考答案：错误错误16. 利用扩充问题求解下列线性规划问题：min f=-x4+2x5+3x6, s.t. x1+5x4-x5+5x6+x7=17, x2-x4+2x5-x6+x7=-22,利用扩充问题求解下列线性规划问题：min f=-x4+2x5+3x6,s.t. x1+5x4-x5+5x6+x7=17,x2-x4+2x5-x6+x7=-22,x3+x4+x5-x6+x7=-33,xi0(i=1，2，7)添加人工约束：x4+x5+x6+x7=M，对扩充问题迭代两次得表7，从表中x2的对应行可知问题无可行解表7 x1 x5 x6 x7 f -frac175 -frac15-frac95-4-frac15 x8 x2x3x4 M-frac175-22+frac175-33-frac175frac175 -frac15 frac65 0 frac45frac15 frac95 0 frac65-frac15 frac65-2 frac45frac15-frac15 1 frac1517. 求抛物线y24x上的点，使它与直线xy4O相距最近求抛物线y24x上的点，使它与直线xy4O相距最近正确答案：18. 2一平面经过原点和另一点(6，3，2)且与平而5x+4y-3z=8垂直，求此平面方程。2一平面经过原点和另一点(6，3，2)且与平而5x+4y-3z=8垂直，求此平面方程。2-17x+28y+9=019. (1)设f(x)=sinx,，试证在点x=0处fg(x)连续 (2)讨论函数在定义域内是否连续(1)设f(x)=sinx,，试证在点x=0处fg(x)连续(2)讨论函数在定义域内是否连续(1)由题意有因此fg(x)处处连续，自然fg(x)也在x=0点处连续 (2)当0xe时，有当xe时，有于是有又由于可知f(x)在x-=e点连续，从而f(x)的定义域x0上连续 20. 不能被5整除的数是A、115.0B、220.0C、323.0D、425.0不能被5整除的数是A、115.0B、220.0C、323.0D、425.0正确答案：C21. VE中两组标准正交基之间的过渡矩阵，必为正交矩阵 VE中两组正交基的过渡矩阵为正交矩阵？VE中两组标准正交基之间的过渡矩阵，必为正交矩阵VE中两组正交基的过渡矩阵为正交矩阵？例设VE=R3=(a，b，c)|a，b，cR，1=(2，1，1)，2=(0，3，0)，3=(1，0，-2)；1=(1，1，0)，2=(1，-1，0)，3=(0，0，1)是两组正交基，且，，不为正交矩阵 22. 从点(2，0)引两条直线与曲线y=x3相切，求由此两条切线与曲线y=x3所围图形的面积从点(2，0)引两条直线与曲线y=x3相切，求由此两条切线与曲线y=x3所围图形的面积如下图所示，设切点为(x0，)，则切线斜率为3，切线方程为y= 因为切线过(2，0)点，所以有，解得x0=0，x0=3 即切点坐标为：(0，0)，(3，27)，相应的两条切线方程为 y=0，y=27x-54 选积分变量为y，则所求面积为 = 23. 求解线性规划问题 min f=3x12x2x3, stx12x2x3=15， 2x15x3=18， 2x14x2x3x4=10, xj0(j=1，2，3求解线性规划问题minf=3x1+2x2+x

曲线sin(xy)+ln(y-x)=x在点(0，1)处的切线方程是________.

答案：1、y=x+1.

解析：

先求曲线sin(xy)+ln(y-x)=x在点(0，1)处切线斜率y'(0).等式sin(xy)+ln(y-x)=x两端对x求导得

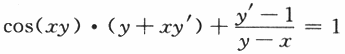
在上式中令x=0，y=1得y'(0)=1，于是该曲线在点(0，1)处的切线方程为y-1=x，即y=x+1.

为使铁路直线与圆曲线顺畅连接，应在直线与圆曲线之间加入缓和曲线，设圆曲线外轨抬高为h₀，关于缓和曲线以下说法正确的是()

A:HY点处缓和曲线曲率半径为R，外轨抬高为0
B:HY点处缓和曲线曲率半径为∞，外轨抬高为h₀
C:HY点处缓和曲线曲率半径为R，外轨抬高为h₀
D:HY点处缓和曲线曲率半径为∞，外轨抬高为0

答案：C

解析：

h₀点指圆缓点，是圆曲线连接缓和曲线的，圆缓点处缓和曲线曲率半径为R，外轨抬高为h₀。

为使铁路直线与圆曲线顺畅连接，应在直线与圆曲线之间加入缓和曲线，设圆曲线外轨抬高为ho，关于缓和曲线以下说法正确的是 ( )

A． HY点处缓和曲线曲率半径为R，外轨抬高为0
B．HY点处缓和曲线曲率半径为无穷大，外轨抬高为h0
C．HY点处缓和曲线曲率半径为R，外轨抬高为h0
D．HY点处缓和曲线曲率半径为无穷大，外轨抬高为0

答案：C

解析：

h。点指圆缓点，是圆曲线连接缓和曲线的，圆缓点处缓和曲线曲率半径为R，外轨抬高为h0。

为使铁路直线与圆曲线顺畅连接，应在直线与圆曲线之间加入缓和曲线，设圆曲线外轨抬高为ho，关于缓和曲线以下说法正确的是 ( )

答案：C

解析：

h。点指圆缓点，是圆曲线连接缓和曲线的，圆缓点处缓和曲线曲率半径为R，外轨抬高为h0。

为使铁路直线与圆曲线顺畅连接，应在直线与圆曲线之间加入缓和曲线，设圆曲线外轨抬高为h₀，关于缓和曲线以下说法正确的是()

答案：C

解析：

h₀点指圆缓点，是圆曲线连接缓和曲线的，圆缓点处缓和曲线曲率半径为R，外轨抬高为h₀。

福建师范大学22春《复变函数》在线作业三及答案参考64

更多 “福建师范大学22春《复变函数》在线作业三及答案参考64” 相关考题

相关内容

最新试卷

热门试卷