若函数的反函数的图像经过点P，则点P的坐标是（　　）A.(1，2) B.(2，1) C.(2，5) D.(5，2)

题目
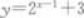若函数的反函数的图像经过点P，则点P的坐标是（　　）

A.(1，2)
B.(2，1)
C.(2，5)
D.(5，2)
相似考题

1.在百分位数分析中,若把P2.5点、P97.5点标在一个数轴上,则()。A、P50点一定在P2.5点与P97.5点之间的中点B、P50点一定靠近P2.5点C、P50点一定靠近P97.5点D、以上都不是

2.（2）若△P1OA1与△P2A1A2均为等边三角形，求此反比例函数的解析式及A2点的坐标

3.力F对某点p的矩不为0,则力F的()p。A、作用点为B、作用点不为C、作用线经过D、作用线不经过

4.若反比例函数的图象经过点A(-2,1) ,则它的表达式是 _________________ ．

更多“若函数的反函数的图像经过点P，则点P的坐标是（　　）”相关问题

  • 第1题：

    下面程序的输出结果是()。include using namespace std;class point {public:point(in

    下面程序的输出结果是( )。 #include ＜iostream＞ using namespace std; class point { public: point(int px=10,int py=10){ x=px;y=py;} getpx( ) { return x;} getpy( ) { return y;} private: int x,y; }; void main(voiD) { point p,q(15,15); cout＜＜"p点的坐标是:"＜＜p. getpx( )＜＜" ,"; cout＜＜p. getpy( )＜＜endl; cout＜＜"q点的坐标是:"＜＜q. getpx( )＜＜" ,"; cout＜＜q. getpy( ); }

    A．p点的坐标是:10,10 q点的坐标是:15,15

    B．p点的坐标是:0,0 q点的坐标是:15,15

    C．p点的坐标是:0,0 q点的坐标是:0,0

    D．p点的坐标是:10,10 q点的坐标是:10,10


    正确答案：A
    解析：此题是给构造函数的参数赋初值。在创建对象时，若对象不带参数，则类中变量的值为构造函数的初值；若创建对象时又给对象带了值，则用此值代替初值。

  • 第2题：

    在平面直角坐标系中选择一些横、纵坐标满足下面条件的点，标出它们的位置，看看它们在第几象限或哪条坐标轴上：

    （1）点P（x，y）的坐标满足xy＞0；

    （2）点P（x，y）的坐标满足xy＜0；

    （3）点P（x，y）的坐标满足xy=0；


    （1）在第一、三象限的点P（x，y）的坐标满足xy＞0；

    （2）在第二、四象限的点P（x，y）的坐标满足xy0；

    （3）在x轴上或者y轴上的点P（x，y）的坐标满足xy=0；


  • 第3题：

    若函数z=f（x，y）在点P0（x0，y0）处可微，则下面结论中错误的是（　　）。



    答案：D
    解析：
    二元函数z=f（x，y）在点（x0，y0）处可微，可得到如下结论：①函数在点（x0，y0）处的偏导数一定存在，C项正确；②函数在点（x0，y0）处一定连续，AB两项正确；可微，可推出一阶偏导存在，但一阶偏导存在不一定一阶偏导在P0点连续，也有可能是可去或跳跃间断点，故D项错误。

  • 第4题：

    如图所示，已知A，B为直线L：y=mx-m+2与抛物线y=x2的两个交点。
    (1)直线ι经过一个定点C，试求出点C的坐标；(2分)
    (2)若m=-1，已知在直线L下方的抛物线上存在一点P(点P与坐标原点0不重合)，且△ABP的面积为（3√13）/2，求点P的坐标。(6分)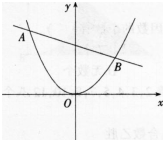


    答案：
    解析：
    (1)直线L：y=m(x-1)+2，当x=1时，y的取值与m无关，此时y=2，所以直线过定点(1，2)；

  • 第5题：

    若函数f(x)＝log2(5x＋1)，则其反函数y＝f－1(x)的图像过点（　　）

    A.(2，1)
    B.(3，2)
    C.(2，3)
    D.(4，3)

    答案：D
    解析：
    反函数与原函数的．27与y互换．把x＝3，y＝4代入，f(x)成立。 故反函数过点(4，3)．(答案为D)

  • 第6题：

    已知函数(x)=ax2+b的图像经过点(1，2)且其反函数-1(x)的图像经过点(3，0)，则函数(x)的解析式是( )

    A.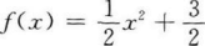
    B.(x)=-x2+3
    C.(x)=3x2+2
    D.(x)=x2+3


    答案：B
    解析：
    【考情点拨】本题主要考查的知识点为反函数的性质． 【应试指导】∵(x)的反函数-1(x)过(3，O)，所以(x)又过点(0，3)所以有(1)=2，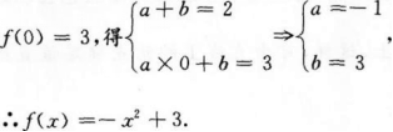

  • 第7题：

    已知直线／：ax+y=1在矩阵对应的变换作用下变为直线Z：x+by=l
    (1)求实数a，b的值；
    (2)若点P(x。，yo)在直线Z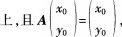求点P的坐标。


    答案：
    解析：
    (1）
    (2)

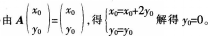
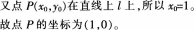
  • 第8题：

    已知一次函数的图像过点（3，5）与（-4，-9），则该函数的图像与y轴交点的坐标为（0，-1）。


    正确答案:正确

  • 第9题：

    有一点实体，其矢量坐标为P（9.5，15.6），若网格的宽与高都是2，则P点栅格化的行列坐标为（）。

    • A、P（5，8）
    • B、P（8，5）
    • C、P（4，7）
    • D、P（7，4）

    正确答案:B

  • 第10题：

    填空题
    二次函数的图像与x轴交点横坐标为－2和1，且通过点（2，4），则其函数解析式为____．

    正确答案： y=x2+x-2
    解析：
    设函数解析式为y＝ax2＋bx＋c，将三个点（－2，0）（1，0）（2，4）代入求解，得到a＝1，b＝1，c＝－2；所以函数解析式为y＝x2＋x－2．

  • 第11题：

    单选题
    有一点实体P，其矢量坐标为P（16.5，13.4），若网格的宽与高都是3，则P点栅格化的行列坐标为（）
    A

    P（6，4）

    B

    P（4，6）

    C

    P（5，6）

    D

    P（6，5）


    正确答案： B
    解析： 暂无解析

  • 第12题：

    单选题
    有一点实体，其矢量坐标为P（9.5，15.6），若网格的宽与高都是2，则P点栅格化的行列坐标为（）。
    A

    P（5，8）

    B

    P（8，5）

    C

    P（4，7）

    D

    P（7，4）


    正确答案： C
    解析： 矢量格式下的任意点(x，y)，所在的网格编号为(i，j)，其中i=INT(x/Lw)j=NT(y/Lw)。图件中网格格式下，网格(i，j)的中心点在矢量格式下的坐标为：Xc=j，Lw+Lw/2；Yc=i，Lw+Lw/2。通过计算得P(8，5)。故选B。

  • 第13题：

    若B点的坐标为(500.000,500.000)m,BP平距、方位角分别为100.000m和60°00'00²,则P点的纵坐标()m。

    A.450.000

    B.500.000

    C.550.000

    D.586.603


    答案：C

  • 第14题：

    已知函数f(x)=a2+k的图象经过点(1，7)，且其反函数f-1(x)的图像经过点(4，0)，则函数f(x)的表达式是 （ ）

    A．f(x)=4x+3

    B．f(x)=2x+5

    C．f(x)=5x+2

    D．f(x)=3x+5


    正确答案：A

  • 第15题：

    若函数f(x,y)在闭区域D上连续，下列关于极值点的陈述中正确的是：
    A.f(x,y)的极值点一定是f(x,y)的驻点
    B.如果P0是f(x,y)的极值点，则P0点处B2-AC
    C.如果P0是可微函数f(x,y)的极值点，则在P0点处df=0
    D.f(x,y)的最大值点一定是f(x,y)的极大值点


    答案：C
    解析：
    提示:在题目中只给出f(x,y)在闭区域D上连续这一条件，并未讲函数f(x,y)在P0点是否具有一阶、二阶偏导，而选项A、B判定中均利用了这个未给的条件，因而选项A、B不成立。选项D中f(x,y)的最大值点可以在D的边界曲线上取得，因而不一定是f(x,y)的极大值点，故选项D不成立。
    在选项C中，给出p0是可微函数的极值点这个条件，因而f(x,y)在P0偏导存在，且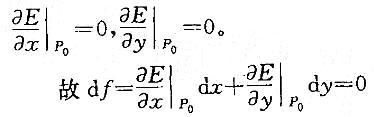

  • 第16题：

    已知动点P在曲线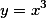上运动，记坐标原点与点P间的距离为l.若点P的横坐标对时间的变化率为常数,则当点P运动到点(1,1)时，l对时间的变化率是


    答案：
    解析：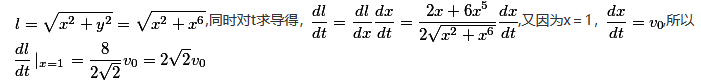

  • 第17题：

    抛物线x2=-16y上一点P到焦点的距离是6，则点P的坐标是( )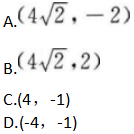


    答案：A
    解析：
    【考情点拨】本题主要考查的知识点为抛物线的定义． 【应试指导】本题应从抛物线的定义去考虑．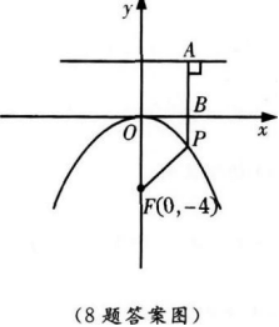


    ∴F(0，-4)，
    ∴准线方程y=4，由题意得｜PF｜=6，
    ∴｜PA｜=6，
    ∵｜AB｜=4，
    ∴｜PB｜=2，
    ∴P点的坐标为(x，-2)，
    ∵P(x，-2)点在抛物线上，
    ∴x2=-16×(-2)=32．

  • 第18题：

    设P是圆x2+y2=2上的一点，该圆在点P的切线平行于直线x+y+2=0，则点P的坐标为



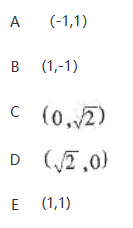    答案：E
    解析：

  • 第19题：

    若函数f(x,y)在闭区域D上连续，下列关于极值点的陈述中正确的是（ ）。
    A. f(x,y)的极值点一定是f(x,y)的驻点
    B.如果P0是f(x,y)的极值点，则P0点处B2-AC)
    C.如果P0是可微函数f(x,y)的极值点，则P0点处df=0
    D.f(x,y)的最大值点一定是f(x,y)的极大值点


    答案：C
    解析：
    提示：如果P0是可微函数f(x,y)的极值点，由极值存在必要条件，在P0点处有

  • 第20题：

    做直线运动的一质点经过P点时的瞬时速度为1m/s，则下列说法中正确的是（）

    • A、它在经过P点后的1s内的位移是1m
    • B、它在经过P点前的1s内的位移是1m
    • C、它在以过P点的时刻为中间时刻的1s内的位移是1m
    • D、若从P点开始匀速行驶1s，它在1s内的位移是1m

    正确答案:D

  • 第21题：

    若函数f（x，y）在闭区域D上连续，下列关于极值点的陈述中正确的是（）。

    • A、f（x，y）的极值点一定是f（x，y）的驻点
    • B、如果P0是f（x，y）的极值点，则P0点处B2-AC<0
    • C、如果P0是可微函数f（x，y）的极值点，则P0点处df=0
    • D、f（x，y）的最大值点一定是f（x，y）的极大值点

    正确答案:C

  • 第22题：

    判断题
    已知一次函数的图像过点（3，5）与（-4，-9），则该函数的图像与y轴交点的坐标为（0，-1）。
    A

    对

    B

    错


    正确答案： 错
    解析： 暂无解析

  • 第23题：

    单选题
    在平面直角坐标系中，如果点P（3a－9，1－a）在第三象限内，且横坐标纵坐标都是整数，则点P的坐标是（　　）。
    A

    （－1，－3）

    B

    （－3，－1）

    C

    （－3，2）

    D

    （－2，－3）


    正确答案： B
    解析：
    点P在第三象限，则横坐标和纵坐标都小于0。即3a－9＜0，1－a＜0，解得1＜a＜3。由于横纵坐标都是整数，所以a是整数，则a＝2。因此P点坐标为（－3，－1）。

相关内容