已知（x-1）²=4，求x的值。

题目

已知（x-1）²=4，求x的值。

相似考题

1.曲线y=x^3＋x－2在点(1,0)处的切线方程是()A、y=2(x-1)B、y=4(x-1)C、y=4x-1D、y=3(x-1)

2.求下列各式中x的值：（1）x3=0.008；（2）x3-3=3/8；（3）（x-1）3=64.

3.求下面函数的返回值（微软）int func(x){int countx = 0;while(x){countx ++;x = x&(x-1);}return countx;}

4.求下列代数式的值：1）-3x²+5x-0.5x²+x-1,其中x=2；2）1/4×(-4x2+2x-8)-(x/2-1),其中1/2; 3）（5a²-3b²）+（a²+b²）-（5a²+3b²），其中a=-1，b=1；4）2（a²b+ab²）-2（a²b -1）-2ab²-2，其中a=-2，b=2.

更多“已知(x－1)²=4,求x的值。 ”相关问题

  • 第1题：

    已知函数(x)=x4-4x+1．
    (1)求(x)的单调区间和极值；
    (2)求曲线y=(x)的凹凸区间．


    答案：
    解析：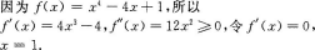

    列表如下，



    由表可知曲线(x)的单调递减区间为(-∞，1)，单调递增区间为(1，+∞)．由于"(x)=12x2≥0，所以为凹曲线，凹区间为(-∞，+∞)，极小值为(1)=1-4+1=-2．

  • 第2题：

    2、求f（x)=x sin（2x-1)在0附近的最小值，相应的命令是（）。

    A．[x,fval] = fminbnd(@(x) x*sin(2*x-1),0,0.5)

    B．[x,fval] = fminsearch(@(x) x*sin(2*x-1),0)

    C．[x,fval] = fminsearch(@(x) x*sin(2*x-1),0.5)

    D．[x,fval] = fminunc(@(x) x*sin(2*x-1),0)


    f′（x）= xcosx-sinx x 2 = x-tanx x 2 cosx ∵0＜x≤1＜ π 2 时，x＜tanx ∴f′（x）＜0，故函数单调递减， 所以当0＜x 1 ＜x 2 ＜1时，f（x 1 ）＞f（x 2 ）即a＞b 故选A

  • 第3题：

    求f（x)=x sin（2x-1)在0附近的最小值，相应的命令是（）。

    A．[x,fval]=fminbnd(@(x) x*sin(2*x-1),0,0.5)

    B．[x,fval]=fminbnd(@(x) x*sin(2*x-1),0)

    C．[x,fval]=fminsearch(@(x) x*sin(2*x-1),[0,0.5])

    D．[x,fval]=fminunc(@(x) x*sin(2*x-1),[0,0.5])


    [x,fval]=fminbnd(@(x) x*sin(2*x-1),0,0.5)

  • 第4题：

    当∣x∣≤4时,函数y=∣x-1∣+∣x-2∣+∣x-3∣的最大值与最小值之差是

    A.4
    B.6
    C.16
    D.20
    E.14

    答案：C
    解析：

  • 第5题：

    求f（x)=x sin（2x-1)在0附近的最小值，相应的命令是（）。

    A．[x,fval] = fminbnd(@(x) x*sin(2*x-1),0,0.5)

    B．[x,fval] = fminsearch(@(x) x*sin(2*x-1),0)

    C．[x,fval] = fminsearch(@(x) x*sin(2*x-1),0.5)

    D．[x,fval] = fminunc(@(x) x*sin(2*x-1),0)


    在 f(x)= 1 x 中，|f（x）|=| 1 x |的最大值是+∞，故①不满足条件； 在f（x）=sin 2 x中，|f（x）|=|sin 2 x|≤1，故②满足条件； 在f（x）=2 -|x| 中，|f（x）|=|2 -|x| |≤1，故③满足条件； 在 f(x)= 1 cotx 中，|f（x）|=| 1 cotx |的最大值是+∞，故④不满足条件． 故答案为：②③．

相关内容