某公司欲购置-台大型机器设备，销售方提出四种付款方案，如下：方案l：第三年年初付款l5万元，然后第六年年末付款25万元。方案2：第一年年初付款l0万元，从第三年开始，每年年初付款5万元，连续支付6次；方案3：第一年年初付款5万元，以后每间隔一个季度付款-次，每次支付2万元，连续支付4年；方案4：前三年不付款，后六年每年初付款7万元。假设该公司的年资本成本率为12%，分别计算四个方案的付款现值，最终确定应该选择哪个方案?((P/F，12%，l)=0．8929，(P/F，12%，2)=0．7972，(P/F，

题目

某公司欲购置-台大型机器设备，销售方提出四种付款方案，如下：

方案l：第三年年初付款l5万元，然后第六年年末付款25万元。

方案2：第一年年初付款l0万元，从第三年开始，每年年初付款5万元，连续支付6次；

方案3：第一年年初付款5万元，以后每间隔一个季度付款-次，每次支付2万元，连续支付4年；

方案4：前三年不付款，后六年每年初付款7万元。

假设该公司的年资本成本率为12%，分别计算四个方案的付款现值，最终确定应该选择哪个方案?((P/F，12%，l)=0．8929，(P/F，12%，2)=0．7972，(P/F，12%，3)=0．7118，(P/F，12%，6)=0．5066，(P/A，12%，4)=3．0373，(P/A，12%，6)=4．1114，(P/A，12%，l6)=6．9740，(P/A，3%，4)=3．7171，(P/A，3%，l6)=12．5611)

相似考题

1.甲公司欲购置一台设备，销售方提出四种付款方案，具体如下：方案1：第一年初付款10万元，从第二年开始，每年末付款28万元，连续支付5次;方案2：第一年初付款5万元，从第二年开始，每年初付款25万元，连续支付6次;方案3：第一年初付款10万元，以后每间隔半年付款一次，每次支付15万元，连续支付8次;方案4：前三年不付款，后六年每年初付款30万元。要求：假设按年计算的折现率为10%，分别计算四个方案的付款现值，最终确定应该选择哪个方案?(计算结果保留两位小数，用万元表示)(P/A，10%，5)=3.7908(P/A，10%，6)=4.3553(P/A，5%，8)=6.4632(P/F，10%，1)=0.9091(P/F，10%，2)=0.8264

2.甲公司欲购置一台设备，卖方提出四种付款方案，具体如下：方案1：第一年初付款10万元，从第二年开始，每年末付款28万元，连续支付5次；方案2：第一年初付款5万元，从第二年开始，每年初付款25万元，连续支付6次；方案3：第一年初付款10万元，以后每间隔半年付款一次，每次支付15万元，连续支付8次；方案4：前三年不付款，后六年每年初付款30万元。假设按年计算的折现率为10%，分别计算四个方案的付款现值，最终确定应该选择哪个方案?

3.某投资者准备购买一套办公用房，有三个付款方案可供选择；（1）甲方案：从现在起每年年初付款10万元，连续支付5年，共计50万元。（2）乙方案：从第3年起，每年年初付款12万元，连续支付5年，共计60万元。（3）丙方案：从现在起每年年末付款11.5万元，连续支付5年，共计57.5万元。假定该公司要求的投资报酬率为10%，通过计算说明应选择哪个方案。

4.某公司拟购置一处房产，房主提出两种付款方案：(1)从现在起，每年年初支付30万，连续支付10次，共300万元；(2)前3年不付款，后7年每年初支付50万元，共350万元。假设该公司的资金成本率(即最低报酬率)为10%，回答下列问题：(1)计算两种付款方式在第10年初的终值，并选择一个合适的方案；(2)计算两种付款方式在第1年初的现值，并选择一个合适的方案。已知：(F/P，10%，9)=2．3579，(F/A，10%，9)=13.579，(F/A，10%，10)=15.937(F/P，10%，6)=1.7716，(F/A，10%，6)=7.7156，(F/A，10%，7)=9.4872(P/A，10%，10)=6.1446，(P/F，10%，3)=0．7513，(P/F，10%，2)=0.8264(P/A，10%，7)=4.8684

更多“某公司欲购置-台大型机器设备，销售方提出四种付款方案，如下：方案l：第三年年初付款l5万元，然后第六年年末付款25万元。方案2：第一年年初付款l0万元，从第三年开始，每年年初付款5万元，连续支付6次；方案3：第一年年初付款5万元，以后每间隔一个季度付款-次，每次支付2万元，连续支付4年；方案4：前三年不付款，后六年每年初付款7万元。假设该公司的年资本成本率为12%，分别计算四个方案的付款现值，最终确定应该选择哪个方案?((P/F，12%，l)=0．8929，(P/F，12%，2)=0．7972，(P/F，”相关问题

  • 第1题：

    2018年年初，某公司购置一条生产线，有以下四种方案。
    方案一：2020年年初一次性支付100万元。
    方案二：2018年至2020年每年年初支付30万元。
    方案三：2019年至2022年每年年初支付24万元。
    方案四：2020年至2024年每年年初支付21万元。
    折现率10%，货币时间价值系数如下表（略）
    要求：（1）计算方案一付款方式下，支付价款的现值；
    （2）计算方案二付款方式下，支付价款的现值；
    （3）计算方案三付款方式下，支付价款的现值；
    （4）计算方案四付款方式下，支付价款的现值；
    （5）选择哪种付款方式更有利于公司。


    答案：
    解析：
    （1）100×（P/F，10%，2）＝82.64（万元）
    　　（2）30＋30×（P/A，10%，2）＝82.07（万元）
    　　（3）24×（P/A，10%，4）＝76.08（万元）
    　　（4）21×（P/A，10%，5）×（P/F，10%，1）＝72.37（万元）
    　　或：21×[（P/A,10%,6）－（P/A,10%,1）]＝72.37（万元）
    　　或：21×（F/A,10%,5）×（P/F,10%,6）＝72.37（万元）
    　　（5）由于方案四的现值最小，所以应该选择方案四

  • 第2题：

    某公司准备购买一套办公用房，有三种付款方案可供选择：
    甲方案：从现在起每年年初付款10万元，连续支付5年，共计50万元；
    乙方案：从第3年起，每年年初付款12万元，连续支付5年，共计60万元；
    丙方案：从现在起每年年末付款11.5万元，连续支付5年，共计57.5万元。
    假定该公司要求的投资报酬率为10%，已知：[（P/A，10%，5）=3.7908，（P/F，10%，1）=0.9091]，根据资料计算下列指标。
    要求：
    某公司准备购买一套办公用房，有三种付款方案可供选择：
    甲方案：从现在起每年年初付款10万元，连续支付5年，共计50万元；
    乙方案：从第3年起，每年年初付款12万元，连续支付5年，共计60万元；
    丙方案：从现在起每年年末付款11.5万元，连续支付5年，共计57.5万元。
    假定该公司要求的投资报酬率为10%，已知：[（P/A，10%，5）=3.7908，（P/F，10%，1）=0.9091]，根据资料计算下列指标。
    要求：
    该公司应选择的付款方案为（　　）。

    A.甲方案
    B.乙方案
    C.丙方案
    D.三个方案一样好

    答案：B
    解析：
    通过计算可知，乙方案的付款总现值最小，所以该公司应选择乙方案。

  • 第3题：

    某公司准备购买一套办公用房，有三种付款方案可供选择：
    甲方案：从现在起每年年初付款10万元，连续支付5年，共计50万元；
    乙方案：从第3年起，每年年初付款12万元，连续支付5年，共计60万元；
    丙方案：从现在起每年年末付款11.5万元，连续支付5年，共计57.5万元。
    假定该公司要求的投资报酬率为10%，已知：[（P/A，10%，5）=3.7908，（P/F，10%，1）=0.9091]，根据资料计算下列指标。
    要求：
    甲方案的付款总现值与丙方案付款总现值的差额为（　　）万元。

    A.-1.89
    B.2.35
    C.-2.21
    D.7.35

    答案：A
    解析：
    丙方案付款总现值=11.5×（P/A，10%，5）=11.5×3.7908=43.59（万元），甲方案与丙方案付款总现值的差额=41.70-43.59=-1.89（万元）

  • 第4题：

    甲公司于 2018年 1月 1日购置一条生产线，有四种付款方案可供选择。
    方案一： 2020年初支付 100万元。
    方案二： 2018年至 2020年每年初支付 30万元。
    方案三： 2019年至 2022年每年初支付 24万元。
    方案四： 2020年至 2024年每年初支付 21万元。
    公司选定的折现率为 10%，部分货币时间价值系数如下表所示。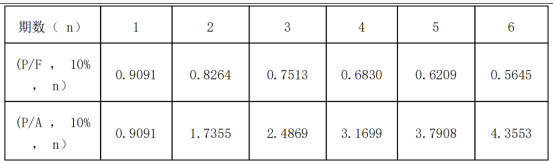

    要求：
    （ 1）计算方案一的现值。
    （ 2）计算方案二的现值。
    （ 3）计算方案三的现值。
    （ 4）计算方案四的现值。
    （ 5）判断甲公司应选择哪种付款方案。


    答案：
    解析：
    （ 1）方案一

    复利现值 =复利终值×复利现值系数 =100×（ P/F， 10%， 2） =100× 0.8264=82.64（万元）
    （ 2）方案二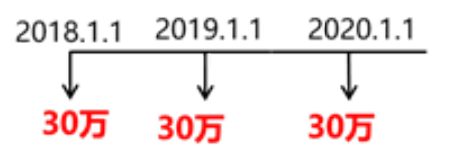

    现值 =30×（ P/A， 10%， 2） +30=30× 1.7355+30=82.07（万元）
    或 ： 现值 =30×（ P/A， 10%， 3）×（ 1+10%） =30× 2.4869× 1.1=82.07（万元）
    （ 3）方案三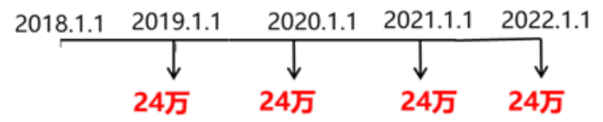

    现值 =24×（ P/A， 10%， 4） =24× 3.1699=76.08（万元）
    （ 4）方案四

    现值 =21×（ P/A， 10%， 5）×（ P/F， 10%， 1） =21× 3.7908× 0.9091=72.37（万元）
    （ 5）因为方案四的现值最小，所以甲公司应选择方案四的付款方案。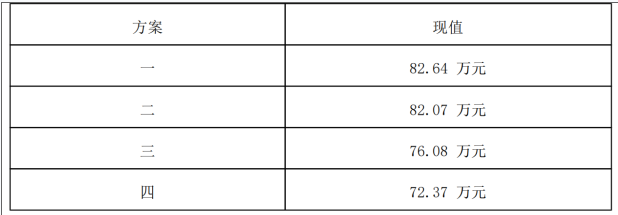

  • 第5题：

    （2018年）2018年年初，某公司购置一条生产线，有以下四种方案。
    　　方案一：2020年年初一次性支付100万元。
    　　方案二：2018年至2020年每年年初支付30万元。
    　　方案三：2019年至2022年每年年初支付24万元。
    　　方案四：2020年至2024年每年年初支付21万元。
    　　货币时间价值系数如下表（略）折现率为10%
    　　要求：
    　　（1）计算方案一付款方式下，支付价款的现值；
    　　（2）计算方案二付款方式下，支付价款的现值；
    　　（3）计算方案三付款方式下，支付价款的现值；
    　　（4）计算方案四付款方式下，支付价款的现值；
    　　（5）选择哪种付款方式更有利于公司。


    答案：
    解析：
    　　（1）100×（P/F，10%，2）＝82.64（万元）
    　　（2）30＋30×（P/A，10%，2）＝82.07（万元）
    　　（3）24×（P/A，10%，4）＝76.08（万元）
    　　（4）21×（P/A，10%，5）×（P/F，10%，1）＝72.37（万元）
    　　（5）由于方案四的现值最小，所以应该选择方案四。@##

  • 第6题：

    （2018年）甲公司于2018年1月1日购置一条生产线，有四种付款方案可供选择。
    方案一：2020年初支付100万元。
    方案二：2018年至2020年每年初支付30万元。
    方案三：2019年至2022年每年初支付24万元。
    方案四：2020年至2024年每年初支付21万元。
    公司选定的折现率为10%。
    部分货币时间价值系数表



    要求：
    （1）计算方案一的现值。
    （2）计算方案二的现值。
    （3）计算方案三的现值。
    （4）计算方案四的现值。
    （5）判断甲公司应选择哪种付款方案。


    答案：
    解析：
    （1）方案一的现值=100×（P/F，10%，2）=100×0.8264=82.64（万元）
    （2）方案二的现值=30×（P/A，10%，3）×（1+10%）=30×2.4869×（1+10%）=82.07（万元）
    （3）方案三的现值=24×（P/A，10%，4）=24×3.1699=76.08（万元）
    （4）方案四的现值=21×（P/A，10%，5）×（P/F，10%，1）=21×3.7908×0.9091=72.37（万元）
    （5）因为方案四的现值最小，所以甲公司应选择方案四的付款方案。

  • 第7题：

    某公司有一项付款业务，有甲乙丙三种付款方式可供选择。 甲方案：现在支付30万元，一次性结清； 乙方案：分5年付款，各年初的付款为6万元， 丙方案首付4万元，以后每年末付款6万元，连付5年。年利率为10%。 要求：按现值计算，选择最优方案。


    正确答案: 乙方案：6*PVIFA（10%，5）*（1+10%）=6*3.791*1.1=25.02
    丙方案：4+6*PVIFA（10%，5）=26.75
    应选择乙方案

  • 第8题：

    甲公司欲购置一台设备，销售方提出四种付款方案，具体如下。 方案1：第一年年初付款10万元，从第二年开始，每年年末付款28万元，连续支付5次； 方案2：第一年年末付款5万元，从第二年开始，每年年初付款25万元，连续支付6次； 方案3：第一年年初付款20万元，以后每间隔半年付款一次，每次支付15万元，连续支付8次；方案4：前三年不付款，后六年每年年初付款30万元。假设按年计算的折现率为10%。（P/A，10%，5）=3.7908，（P/F，10%，1）=0.9091，（P/A，10%，6）=4.3553，（P/A，5%，8）=6.4632，（P/F，10%，2）=0.8264 根据上述资料，回答下列问题。 如果采用方案1，付款额的现值为（）万元。

    • A、98.46
    • B、102.42
    • C、106.49
    • D、112.28

    正确答案:C

  • 第9题：

    甲公司欲购置一台设备，销售方提出四种付款方案，具体如下。 方案1：第一年年初付款10万元，从第二年开始，每年年末付款28万元，连续支付5次； 方案2：第一年年末付款5万元，从第二年开始，每年年初付款25万元，连续支付6次； 方案3：第一年年初付款20万元，以后每间隔半年付款一次，每次支付15万元，连续支付8次； 方案4：前三年不付款，后六年每年年初付款30万元。假设按年计算的折现率为10%。（P/A，10%，5）=3.7908，（P/F，10%，1）=0.9091，（P/A，10%，6）=4.3553，（P/A，5%，8）=6.4632，（P/F，10%，2）=0.8264 根据上述资料，回答下列问题。 甲公司应该选择（）付款。

    • A、方案1
    • B、方案2
    • C、方案3
    • D、方案4

    正确答案:A

  • 第10题：

    问答题
    李某计划购买一处新房用于结婚，总房价为100万元，开发商提出三种付款方案：　　方案一：分10年付清，每年初付款15万元。　　方案二：首付30万元，剩余款项分10年付清，每年末付款12万元。　　方案三：首付50万元，1至6年每年末付款10万元，7至10年每年末付款3万元。　　已知：（P/A，8%，4）＝3.3121，（P/A，8%，6）＝4.6229，（P/A，8%，9）＝6.2469，（P/A，8%，10）＝6.7101，（P/F，8%，6）＝0.6302，（F/P，8%，4）＝1.3605，（F/P，8%，10）＝2.1589，（F/A，8%，4）＝4.5061，（F/A，8%，6）＝7.3359，（F/A，8%，10）＝14.487　　要求：　　（1）假定银行利率为8%，分别计算三个方案的现值并确定最优付款方案。　　（2）假定银行利率为8%，分别计算三个方案的终值并确定最优付款方案。

    正确答案：
    (1)方案一的现值=15+15×(P/A,8%,9)=15+15×6.2469=108.70(万元)
    方案二的现值=30+12×(P/A,8%,10)=30+12×6.7101=110.52(万元)
    方案三的现值=50+10×(P/A,8%,6)+3×(P/A,8%,4)×(P/F,8%,6)=50+10×4.6229+3×3.3121×0.6302=102.49(万元)
    经过计算,方案三的付款现值最小,应该选择方案三。
    (2)方案一的终值=15×(F/A,8%,10)×(1+8%)=15×14.487×(1+8%)=234.69(万元)
    方案二的终值=12×(F/A,8%,10)+30×(F/P,8%,10)=12×14.487+30×2.1589=238.61(万元)
    方案三的终值=50×(F/P,8%,10)+10×(F/A,8%,6)×(F/P,8%,4)+3×(F/A,8%,4)=50×2.1589+10×7.3359×1.3605+3×4.5061=221.27(万元)
    经过计算,方案三的付款终值最小,应该选择方案三。
    解析： 暂无解析

  • 第11题：

    问答题
    计算分析题： 某投资者准备购买一套办公用房，有三个付款方案可供选择： （1）甲方案：从现在起每年年初付款24万元，连续支付5年，共计120万元； （2）乙方案：从第3年起，每年年初付款26万元，连续支付5年，共计130万元； （3）丙方案：从现在起每年年末付款25万元，连续支付5年，共计125万元。 假定该公司要求的投资报酬率为10%，通过计算说明应选择哪个方案。

    正确答案： 甲方案：
    付款总现值=24×（P/A，10%，5）×（1+10%）=24×3.7908×（1+10%）=100.08（万元）。
    乙方案：
    付款总现值=26×（P/A，10%，5）×（P/F，10%，1）=26×3.7908×0.9091=89.60（万元）。
    丙方案：
    付款总现值=25×（P/A，10%，5）=25×3.7908=94.77（万元）。
    通过计算可知，该公司应选择乙方案。
    解析： 暂无解析

  • 第12题：

    问答题
    计算分析题：甲公司欲购置－台设备，销售方提出四种付款方案，具体如下：方案1：第－年初付款10万元，从第二年开始，每年末付款28万元，连续支付5次； 方案2：第－年初付款5万元，从第二年开始，每年初付款25万元，连续支付6次； 方案3：第－年初付款10万元，以后每间隔半年付款－次，每次支付15万元，连续支付8次； 方案4：前三年不付款，后六年每年初付款30万元。 要求：假设按年计算的折现率为10％，分别计算四个方案的付款现值，最终确定应该选择哪个方案(计算结果保留两位小数，用万元表示)

    正确答案： 方案1的付款现值
    ＝10＋28×(P／A，10％，5)X(p／F，10％，1)
    ＝10＋28×3．7908×0．9091
    ＝106．49(万元)
    方案2的付款现值
    ＝5＋25×(P／A，10％，6)
    ＝5＋25×4．3553
    ＝113．88(万元)
    方案3的付款现值
    ＝10＋15×(P／A，5％，8)
    ＝10＋15×6．4632
    ＝106．95(万元)
    方案4的付款现值
    ＝30×(P／A，10％，6)×(P／F，10％，2)
    ＝30×4．3553×0．8264
    ＝107．98(万元)
    由于方案1的付款现值最小，所以应该选择方案1。
    解析： 暂无解析

  • 第13题：

    某公司拟购置一房产，房主提出三种付款方案：
    　　（1）从现在起，每年年初支付20万，连续支付10次，共200万元；
    　　（2）从第5年开始，每年年末支付25万元，连续支付10次，共250万元；
    　　（3）从第5年开始，每年年初支付24万元，连续支付10次，共240万元。
    　　假设该公司的资金成本率（即最低报酬率）为10%，你认为该公司应选择哪个方案？


    答案：
    解析：
    方案（1）
    　　P＝20＋20×（P/A，10%，9）＝20＋20×5.759＝135.18（万元）
    　　方案（2）
    　　P＝25×（P/A，10%，10）×（P/F，10%，4）＝104.92（万元）　　
    　　方案（3）
    　　P＝24×[（P/A，10%，13）－（P/A，10%，3）]＝24×（7.103－2.487）＝110.78（万元）

  • 第14题：

    某公司准备购买一套办公用房，有三种付款方案可供选择：
    甲方案：从现在起每年年初付款10万元，连续支付5年，共计50万元；
    乙方案：从第3年起，每年年初付款12万元，连续支付5年，共计60万元；
    丙方案：从现在起每年年末付款11.5万元，连续支付5年，共计57.5万元。
    假定该公司要求的投资报酬率为10%，已知：[（P/A，10%，5）=3.7908，（P/F，10%，1）=0.9091]，根据资料计算下列指标。
    要求：
    （1）甲方案的付款总现值为（　　）万元。

    A.41.70
    B.41.35
    C.43.59
    D.47.10

    答案：A
    解析：
    甲方案付款总现值=10×（P/A，10%，5）×（1+10%）=10×3.7908×（1+10%）=41.70（万元）

  • 第15题：

    （2018年） 2018年年初，某公司购置一条生产线，假设利率为10%，有以下四种方案。
    　　方案一：2020年年初一次性支付100万元。
    　　方案二：2018年至2020年每年年初支付30万元。
    　　方案三：2019年至2022年每年年初支付24万元。
    　　方案四：2020年至2024年每年年初支付21万元。
    　　已知：

    要求：
    　　（1）计算方案一付款方式下，支付价款的现值；
    　　（2）计算方案二付款方式下，支付价款的现值；
    　　（3）计算方案三付款方式下，支付价款的现值；
    　　（4）计算方案四付款方式下，支付价款的现值；
    　　（5）选择哪种付款方式更有利于公司。


    答案：
    解析：
    （1）100×（P/F，10%，2）＝100×0.8264＝82.64（万元）
    　　（2）30＋30×（P/A，10%，2）＝30＋30×1.7355＝82.07（万元）
    　　或：30×（P/A，10%，3）×（1＋10%）＝30×2.4869×1.1＝82.07（万元）
    　　（3）24×（P/A，10%，4）＝24×3.1699＝76.08（万元）
    　　（4）21×（P/A，10%，5）×（P/F，10%，1）＝21×3.7908×0.9091＝72.37（万元）
    　　（5）由于方案四的现值最小，所以应该选择方案四。

  • 第16题：

    （2018年）甲公司于 2018年 1月 1日购置一条生产线，有四种付款方案可供选择。
    方案一： 2020年初支付 100万元。
    方案二： 2018年至 2020年每年初支付 30万元。
    方案三： 2019年至 2022年每年初支付 24万元。
    方案四： 2020年至 2024年每年初支付 21万元。
    公司选定的折现率为 10%，部分货币时间价值系数如下表所示。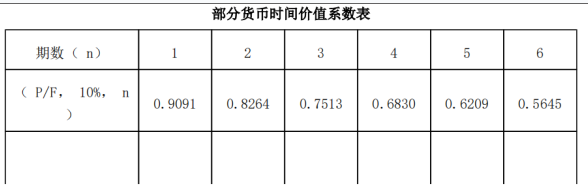


    要求：
    （ 1）计算方案一的现值。
    （2）计算方案二的现值。
    （ 3）计算方案三的现值。
    （ 4）计算方案四的现值。
    （ 5）判断甲公司应选择哪种付款方案。


    答案：
    解析：
    （ 1）方案一的现值 =100×（ P/F， 10%， 2） =100× 0.8264=82.64（万元）
    （ 2）方案二的现值 =30×（ P/A， 10%， 3）×（ 1+10%） =30× 2.4869×（ 1+10%） =82.07（万元）
    （ 3）方案三的现值 =24×（ P/A， 10%， 4） =24× 3.1699=76.08（万元）
    （ 4）方案四的现值 =21×（ P/A， 10%， 5）×（ P/F， 10%， 1） =21× 3.7908× 0.9091=72.37（万元）
    （ 5）因为方案四的现值最小，所以甲公司应选择方案四的付款方案。

  • 第17题：

    （2018年）2018年年初，某公司购置一条生产线，有以下四种方案。
    　　方案一：2020年年初一次性支付100万元。
    　　方案二：2018年至2020年每年年初支付30万元。
    　　方案三：2019年至2022年每年年初支付24万元。
    　　方案四：2020年至2024年每年年初支付21万元。
    　　货币时间价值系数如下表（略）
    　　要求：（1）计算方案一付款方式下，支付价款的现值；
    　　（2）计算方案二付款方式下，支付价款的现值；
    　　（3）计算方案三付款方式下，支付价款的现值；
    　　（4）计算方案四付款方式下，支付价款的现值；
    　　（5）选择哪种付款方式更有利于公司。


    答案：
    解析：
    （1）100×（P/F，10%，2）＝82.64（万元）
    　　（2）30＋30×（P/A，10%，2）＝82.07（万元）
    　　（3）24×（P/A，10%，4）＝76.08（万元）
    　　（4）21×（P/A，10%，5）×（P/F，10%，1）＝72.37（万元）
    　　（5）由于方案四的现值最小，所以应该选择方案四。

  • 第18题：

    甲公司欲购置一台设备，销售方提出四种付款方案，具体如下。 方案1：第一年年初付款10万元，从第二年开始，每年年末付款28万元，连续支付5次； 方案2：第一年年末付款5万元，从第二年开始，每年年初付款25万元，连续支付6次； 方案3：第一年年初付款20万元，以后每间隔半年付款一次，每次支付15万元，连续支付8次； 方案4：前三年不付款，后六年每年年初付款30万元。假设按年计算的折现率为10%。（P/A，10%，5）=3.7908，（P/F，10%，1）=0.9091，（P/A，10%，6）=4.3553，（P/A，5%，8）=6.4632，（P/F，10%，2）=0.8264 根据上述资料，回答下列问题。 如果采用方案2，付款额的现值为（）万元。

    • A、102.42
    • B、106.49
    • C、113.43
    • D、113.88

    正确答案:C

  • 第19题：

    云达科技公司拟购置一设备，供方提出两种付款方案：  （1）从现在起，每年年初支付200万元，连续支付10次，共2000万元；  （2）从第5年开始，每年年初支付250万元，连续支付10次，共2500万元。  假设公司的资金成本率（即最低报酬率）为10%，你认为云达科技公司应选择哪个付款方案？


    正确答案: 第一种付款方案是计算即付年金的现值。根据即付年金的现值的计算方法，有
    P0=200×[（P/A，10%，10-1）+1]=200×（5.759+1）=1351.8（万元）
    第二种付款方案是计算递延年金的现值。其计算方法或思路有以下几种：
    第1种方法：
    P0=250×（P/A，10%，10）×（P/S，10%，3）=250×6.145×0.7513=1154.11（万元）
    第2种方法：
    P0=250×[（P/A，10%，3+10）-（P/A，10%，3）]=250×[7.1034-2.4869]=1154.125（万元）
    第3种方法：（即利用即付年金现值的计算思路进行计算）
    P0=250×[（P/A，10%，10-1）+1]×（P/S，10%，4）=250×[5.7590+1]×0.6830=1154.099（万元）
    答：该公司应选择第（2）种付款方案。

  • 第20题：

    甲公司欲购置一台设备，销售方提出四种付款方案，具体如下。 方案1：第一年年初付款10万元，从第二年开始，每年年末付款28万元，连续支付5次； 方案2：第一年年末付款5万元，从第二年开始，每年年初付款25万元，连续支付6次； 方案3：第一年年初付款20万元，以后每间隔半年付款一次，每次支付15万元，连续支付8次； 方案4：前三年不付款，后六年每年年初付款30万元。假设按年计算的折现率为10%。（P/A，10%，5）=3.7908，（P/F，10%，1）=0.9091，（P/A，10%，6）=4.3553，（P/A，5%，8）=6.4632，（P/F，10%，2）=0.8264 根据上述资料，回答下列问题。 如果采用方案3，付款额的现值为（）万元。

    • A、102.49
    • B、116.95
    • C、112.46
    • D、113.88

    正确答案:B

  • 第21题：

    问答题
    A公司20X7年12月10日欲购置一批电脑，销售方提出三种付款方案，具体如下：方案1：20X7年12月10日付款10万元，从20X9年开始，每年12月10日付款28万元，连续支付5次；方案2：20X7年12月10日付款5万元，从20X8年开始，每年12月10日付款25万元，连续支付6次；方案3：20X7年12月10日付款10万元，从20X8年开始，6月10日和12月10日付款，每次支付15万元，连续支付8次。假设A公司的投资收益率为10%，A公司应该选择哪个方案？

    正确答案：
    解析：

  • 第22题：

    问答题
    某投资者准备购买一套办公用房，有3个付款方案可供选择：(1)甲方案：从现在起每年初付款10万元，连续支付5年，共计50万元。(2)乙方案：从第3年起，每年初付款12万元，连续支付5年，共计60万元。(3)丙方案：从现在起每年末付款11.5万元，连续支付5年，共计57. 5万元。假定该投资者要求的投资报酬率为10%，通过计算说明应选择哪个方案。

    正确答案：
    解析：

  • 第23题：

    问答题
    某公司有一项付款业务，有甲乙丙三种付款方式可供选择。甲方案：1～5年每半年末付款2万元，共20万元；乙方案：1～5年每年年初付款3.8万元，共19万元；丙方案：三年后每年年初付款7.5万元，连续支付三次，共22.5万元。假定该公司股票的β系数为0.75，平均股票要求的收益率为12.5%，无风险收益率为2.5%，请替该公司做出付款方式的决策。

    正确答案： 公司股票的必要收益率=2.5%+0.75×（12.5%-2.5%）=10%
    P甲=2×（P/A，5%，10）=2×7.7217=15.4434（万元）
    P乙=3.8+3.8×（P/A，10%，4）=3.8+3.8×3.1699=15.8456（万元）
    P丙=7.5×［（P/A，10%，5）-（P/A，10%，2）］=7.5×（3.7908-1.7355）=15.4148（万元）
    因为P丙甲乙，所以该公司应选择丙方案。
    解析： 暂无解析

相关内容