输入n*n的矩阵，判断其是否为对称阵，即判断其上三角阵与下三角阵对应元素是否都相等。

题目

输入n*n的矩阵，判断其是否为对称阵，即判断其上三角阵与下三角阵对应元素是否都相等。

相似考题

1.可对角化的矩阵是____。A.实对称阵B.有n个相异特征值的n阶阵C.有n个线性无关的特征向量的n阶方阵

2.若把A分解成一个下三角阵L和一个单位上三角阵U的乘积，称为克洛特(Crout)分解。()

3.将非奇异阵A分解成一个下三角阵L和一个上三角阵U的乘积：A=LU称为对矩阵A的三角分解。()

4.● 已知对称矩阵 An*n（Ai,j=Aj,i）的主对角线元素全部为0，若用一维数组B 仅存储矩阵 A 的下三角区域的所有元素（不包括主对角线元素），则数组 B的大小为（40）。（40）A.n(n-1)B.n2/2C.n(n-1)/2D.n(n+1)/2

更多“输入n*n的矩阵，判断其是否为对称阵，即判断其上三角阵与下三角阵对应元素是否都相等。”相关问题

  • 第1题：

    下列不属于节点导纳矩阵特点的是()。

    A.n×n维方程

    B.对称阵

    C.高度稀疏矩阵

    D.上三角矩阵


    答案：D

  • 第2题：

    简单无向图的邻接矩阵是对称的，可以对其进行压缩存储。若无向图G有n个节点，其邻接矩阵为A[1..n, 1..n]，且压缩存储在B[1..k]中，则k的值至少为(30)。若按行压缩存储对称矩阵的上三角元素，则当n等于10时，边(V6，V3)的信息存储在B[(31)]中。

    A．n(n+1)/2

    B．n2/2

    C．(n-1)(n+1)/2

    D．n(n-1)/2


    正确答案：D

  • 第3题：

    下列程序的功能是( )。 main() { static int s[3][3]={1，2，3，4，5，6，7，8，9，)，m，n； for(m=0；m＜3；m++) { for(n=0；n＜=m；n++) printf("%d"，s[m][n])；printf("\n')； } }

    A．输出3×3矩阵的下三角的元素

    B．输出3×3矩阵的上三角的元素

    C．输出3×3矩阵的对角线上的元素

    D．输出3×3矩阵的元素


    正确答案：A
    解析：本题使用了一个双重for循环，外循环变量m的变化范围是0～2，而内循环变量n的变化范围从0～m，所以执行循环体时(m，n)的值依次为(0，0)，(1，0)，(1，1)，(2，0)，(2，1)，(2，2)，故输出的是3×3矩阵的下三角元素。所以应该选择A。

  • 第4题：

    设A为n阶实对称矩阵,下列结论不正确的是().

    A.矩阵A与单位矩阵E合同
    B.矩阵A的特征值都是实数
    C.存在可逆矩阵P,使P^-1AP为对角阵
    D.存在正交阵Q,使Q^TAQ为对角阵

    答案：A
    解析：
    根据实对称矩阵的性质，显然(B)、(C)、(D)都是正确的，但实对称矩阵不一定是正定矩阵，所以A不一定与单位矩阵合同，选(A).

  • 第5题：

    设A,B都是n阶对称阵,证明AB是对称阵的充要条件是AB=BA.


    答案：
    解析：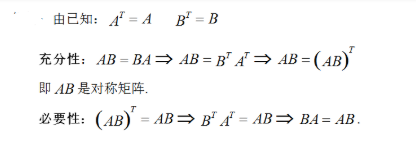

  • 第6题：

    设A=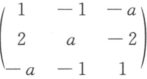,求A的特征值与特征向量,判断矩阵A是否可对角化,若可对角化,求出可逆矩阵P及对角阵.


    答案：
    解析：

  • 第7题：

    简单无向图的邻接矩阵是对称的，可以对其进行压缩存储。若无向图G有n个结点，其邻接矩阵为A[1.n，1.n]，且压缩存储在B[1.n(n-1)/2]。若按行压缩存储对称矩阵的上三角元素，则当n等于10时，边(V6，V3)的信息存储在()。

    A.B[18]
    B.B[19]
    C.B[20]
    D.B[21]

    答案：C
    解析：
    边(V6，V3)与边(V3，V6)是同一条边。原第i行第j列元素在矩阵B(上三角形式)中的下标为：(n-1)+(n-2)+…+(n-(i-1))+(j-i)。将数值代入，(10-1)+(10-2)+(6-3)=20。边(V6，V3)的信息存储在B[20]中。

  • 第8题：

    由高斯消去法说明当Δi≠0（i=1，2，...，n-1）时，则A=LU，其中L为单位下三角阵，U为上三角阵。


    正确答案: 高斯消去法第k步等价于左乘单位下三角矩阵Lk，而顺序主子式均不为零保证所得矩阵对角元不为零，可进行第k+1步消元，U=A（n）=Ln...L1A，A=L1-1...Ln-1U=LU。

  • 第9题：

    n阶对称矩阵，如果只存储下三角元素，只需要（）个存储单元。


    正确答案:n（n-1）/2

  • 第10题：

    设A是n阶方阵（不一定是对称阵）．二次型f（x）=xTAx相对应的对称阵是（）．

    • A、A
    • B、AT
    • C、1/2（A+AT）
    • D、A+AT

    正确答案:C

  • 第11题：

    问答题
    由高斯消去法说明当Δi≠0（i=1，2，...，n-1）时，则A=LU，其中L为单位下三角阵，U为上三角阵。

    正确答案： 高斯消去法第k步等价于左乘单位下三角矩阵Lk，而顺序主子式均不为零保证所得矩阵对角元不为零，可进行第k+1步消元，U=A（n）=Ln...L1A，A=L1-1...Ln-1U=LU。
    解析： 暂无解析

  • 第12题：

    单选题
    设A，B是n阶对称阵，Λ是对角阵，下列矩阵中不是对称阵的是（）．
    A

    A+2E

    B

    A+Λ

    C

    AB

    D

    A-B


    正确答案： A
    解析： 暂无解析

  • 第13题：

    无向图的邻接矩阵是对称的,因此可只存储邻接矩阵的下(或上)三角阵()

    此题为判断题(对，错)。


    参考答案：对

  • 第14题：

    若将N阶对称矩阵A按照行序为主序方式将包括主对角线元素在内的下三角形的所有元素依次存放在一个一维数组B中，则该对称矩阵在B中占用了(40)—个数组元素。(40)

    A．N2

    B．N×(N-1)

    C．N×(N+1)/2

    D．N×(N-1)/2


    正确答案：C
    解析：因为N阶对称矩阵包括主对角线元素在内的下三角形的所有元素一共为N×(N+1)/2，因此应选择C。

  • 第15题：

    简单无向图的邻接矩阵是对称的，可以对其进行压缩存储。若无向图G有n个结点，其邻接矩阵为A[1..n,1..n]，且压缩存储在B[1..k]中，则k的值至少为(40)。若按行压缩存储对称矩阵的上三角元素，则当n等于10时，边(V6,V3)的信息存储在 B[(41)]中。

    A．

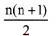
    B．

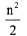
    C．

    D．


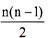    正确答案：D
    解析：具有n个结点的简单无向图的邻接矩阵是对称矩阵。对称矩阵关于主对角线对称，因此只需存储上三角或下三角部分即可。比如，我们只存储上三角中的元素aij，其特点是j≤i且1≤i≤n，对于上三角中的元素aij，它和对应的aij相等，因此当访问的元素在上三角时，直接去访问和它对应的下三角元素即可。这样，原米需要n*n个存储单元，现在只需要n(n+1)/2个存储单元了，由于简单无向图中没有自环，因此主对角线的元素无须存储，因此至少需要n(n-1)/2个存储单元。若按行压缩存储对称矩阵的上三角元素，则第1行需存储n-1个元素，第二行存储n-2个元素，第i行需存储n-i个元素，元素aij(1≤i≤n-1且ij≤n)存储在B[(i-1)n-i(i-1)/2+j-i]中，当n为10，与边(V6,V3)对应的矩阵元素为a3.6，即其信息存储在B[20]中。

  • 第16题：

    设x为n维列向量,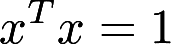,令,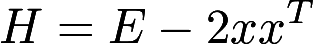证明H是对称的正交阵.


    答案：
    解析：

  • 第17题：

    证明对称阵A为正定的充分必要条件是:存在可逆矩阵U,使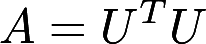,即A与单位阵E合同


    答案：
    解析：

  • 第18题：

    节点导纳矩阵是（ ）。

    A.对称的满阵
    B.对称的稀疏矩阵
    C.不对称的满阵
    D.不对称的稀疏矩阵

    答案：B
    解析：

  • 第19题：

    下列不属于节点导纳矩阵特点的是（）。

    • A、n×n维方程
    • B、对称阵
    • C、高度稀疏矩阵
    • D、上三角矩阵

    正确答案:D

  • 第20题：

    设A为n阶非奇异矩阵且有分解式A=LU，其中L为单位下三角阵，U为上三角阵，求证A的所有顺序主子式均不为零。


    正确答案: 因为A非奇异，U的对角元uii不为零，又LU分解等价于高斯消去法，aii（i）=uii≠0由引理可知，矩阵A的顺序主子式均不为零。

  • 第21题：

    设A，B是n阶对称阵，Λ是对角阵，下列矩阵中不是对称阵的是（）．

    • A、A+2E
    • B、A+Λ
    • C、AB
    • D、A-B

    正确答案:C

  • 第22题：

    问答题
    设A为n阶非奇异矩阵且有分解式A=LU，其中L为单位下三角阵，U为上三角阵，求证A的所有顺序主子式均不为零。

    正确答案： 因为A非奇异，U的对角元uii不为零，又LU分解等价于高斯消去法，aii（i）=uii≠0由引理可知，矩阵A的顺序主子式均不为零。
    解析： 暂无解析

  • 第23题：

    单选题
    设A是n阶方阵（不一定是对称阵）．二次型f（x）=xTAx相对应的对称阵是（）．
    A

    A

    B

    AT

    C

    1/2（A+AT）

    D

    A+AT


    正确答案： C
    解析： 暂无解析

  • 第24题：

    填空题
    n阶对称矩阵，如果只存储下三角元素，只需要（）个存储单元。

    正确答案： n（n-1）/2
    解析： 暂无解析

相关内容