一个四边形的广场它的四边分别是60米、72米、96米、84米，现在要在四边上植树，如果四边上每两棵树的间隔距离相等，那么至少要种多少棵树（）A、20B、22C、24D、26

题目

一个四边形的广场它的四边分别是60米、72米、96米、84米，现在要在四边上植树，如果四边上每两棵树的间隔距离相等，那么至少要种多少棵树（）

  • A、20
  • B、22
  • C、24
  • D、26
相似考题

1.一个四边形广场，它的四边长分别是60米，72米，84米，96米，现在在四边上植树，四角需种树，而且每两棵树的间隔相等，那么，至少要种多少棵树?( )A.22B.25C.26D.30

2.一个四边形广场，它的四边长分别是60米、72米、96米、84米，现在四边上植树，四角需种树，而且每两棵树的间隔相等，那么，至少要种多少棵树?（ ）A．22B．25C．26D．30

3.若顺次连接四边形ABCD各边中点所得四边形是矩形，则四边形ABCD一定是( )。A.对角线相互垂直的四边形 B.矩形 C.对角线相等的四边形 D.菱形

4.如果一个四边形是中心对称图形，那么这个四边形一定是平行四边形吗？为什么？

更多“一个四边形的广场它的四边分别是60米、72米、96米、84米，现”相关问题

  • 第1题：

    一个四边形广场，它的四条边长分别是60米、72米、96米、84米，现在四边和四角需种树，而且每两棵树的间隔相等，那么，至少要种多少棵树?（　　）

    A.22
    B.25
    C.26
    D.30

    答案：C
    解析：
    此题为封闭植树与最大公约数结合的问题。根据题意可知，要使四边上每两棵树间隔距离都相等，这个间隔距离必须能整除每一边长。要种的树尽可能少(间隔距离尽可能大)，就应先求出四条边长的最大公约数。60、72、96、84四数的最大公约数是12，种的棵数至少为(60+72+96+84)÷12=26。所以选C项。

  • 第2题：

    如图7，在四边形ABCD中，AD∥BC，要使四边形ABCD为平行四边形，则应添加的条件是__________（添加一个条件即可）。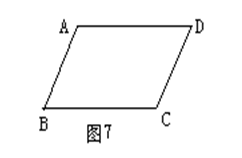


    答案：
    解析：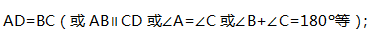

  • 第3题：

    《义务教育教学课程标准（2011年版）》关于平行四边形的性质的教学要求是：探索并证明平行四边形的性质定理——平行四边形的对边以及对角相等，请基于该要求，完成下列教学设计任务：

    （1）设计平行四边形性质的教学目标；（6分）

    （2）设计两种让学生发现平行四边形性质的教学流程；（12分）

    （3）设计平行四边形性质证明的教学流程，使学生领悟证明过程中的教学思想方法。（12分）


    答案：
    解析：
    本题主要以初中数学教学中的重要内容之一“平行四边形的性质定理”为例，平行四边形的性质定理的基础知识，初中数学课程内容、课程标准及实施建议，教学过程的基本要素及教学方法的选择，教学设计中的教学目标、教学过程及教学策略等相关知识，比较综合性地考查学科知识、课程知识、教学知识以及教学技能的基本知识和基本技能。

    （1）新课标倡导三维教学目标，知识与技能目标、过程与方法目标、情感态度与价值观目标。知识与技能目标，是对学生学习结果的描述，即学生同学习所要达到的结果，又叫结果性目标。这种目标一般有三个层次的要求：学懂、学会、能应用。

    过程与方法目标，是学生在教师的指导下，如何获取知识和技能的程序和具体做法，是过程中的目标，又叫程序性目标。这种目标强调三个过程：做中学、学中做、反思。

    情感态度与价值观目标，是学生对过程或结果的体验后的倾向和感受，是对学习过程和结果的主观经验，又叫体验性目标。它的层次有认同、体会、内化三个层次。

    知识与技能目标是过程与方法目标、情感态度与价值观目标的基础；过程与方法目标是实现知识与技能目标的载体，情感态度与价值观目标对其他目标有重要的促进和优化作用。

    （2）让学生发现平行四边形性质的教学流程，可以从不同角度进行设计，如“观察—猜想—验证—归纳”，“动手操作—小组讨论—归纳总结”等，但重要的是让学生在学习过程中进行主动学习，教师只是起到引导的作用，充分体现“学生是主体，教师是主导”的教学理念。

    （3）平行四边形关于边、角的性质定理，即平行四边形的对边以及对角相等，这一定理的证明是通过证明三角形全等来证明对边、对角相等来进行的。注意在平行四边形性质证明的教学流程中，务必使学生领悟证明过程中所用到的转化思想与方法。

  • 第4题：

    例如，“菱形→等边四边形→平行四边形→四边形”这是一个（）过程。

    • A、弱抽象
    • B、浅层抽象
    • C、深层抽象
    • D、强抽象

    正确答案:D

  • 第5题：

    婆罗摩笈多给出的四边形面积公式在只针对（）成立。

    • A、折四边形
    • B、凹四边形
    • C、圆内接四边形
    • D、圆外切四边形

    正确答案:C

  • 第6题：

    单选题
    例如，“菱形→等边四边形→平行四边形→四边形”这是一个（）过程。
    A

    弱抽象

    B

    浅层抽象

    C

    深层抽象

    D

    强抽象


    正确答案： A
    解析： 暂无解析

  • 第7题：

    单选题
    一个三角形和一个平行四边形，面积相等，底也相等，那么三角形和平行四边形的高相比较().
    A

    三角形的高是平行四边形的一半

    B

    相等

    C

    三角形的高是平行四边形的2倍


    正确答案： A
    解析： 暂无解析

  • 第8题：

    单选题
    一个四边形广场，它的四边长分别是60米、72米、96米、84米，现在要在四边上植树，四角需种树，而且每两棵树的间隔相等，那么，至少要种多少棵树？（　　）
    A

    22

    B

    25

    C

    26

    D

    30


    正确答案： A
    解析：
    由题意可知，需要四边长被两棵树之间的间隔整除。60、72、96、84都能被12整除，即60、72、96、84的最大公约数为12。因此至少要种60÷12＋72÷12＋96÷12＋84÷12＝5＋6＋8＋7＝26棵树。

  • 第9题：

    初中数学《平行四边形的判定》

    一、考题回顾



    二、考题解析
    【教学过程】
    (一)引入新课
    提出问题：平行四边形的定义是什么?平行四边形有什么性质?我们可以说怎么样的一个图形是平行四边形呢?除定义之外还有没有其它的方法来判定一个四边形是平行四边形呢?
    由此引出今天学习的内容是《平行四边形的判定》。
    (二)探索新知
    通过前面的学习，我们知道，平行四边形的对边相等，对角相等，对角线互相平分。那么反过来，对边相等或对角线互相平分的四边形是不是平行四边形呢?下面我们就来验证一下。
    实验一：取两长两短的四根木条用小钉铰在一起，做成一个四边形，如果等长的木条成为对边，那么无论如何转动这个四边形，它的形状都是平行四边形;
    实验二：取两根长短不一的细木条，将它们的中点重叠，并用小钉钉在一起，用橡皮筋连接木条的顶点，做成一个四边形。转动两根木条，这个四边形是平行四边形。
    引导学生归纳得出结论：
    两组对边分别相等的四边形是平行四边形;
    两组对角分别相等的四边形是平行四边形;
    对角线互相平分的四边形是平行四边形。
    提问学生：你能根据平行四边形的定义证明它们吗?
    引导学生以“对角线互相平分的四边形是平行四边形”为例，通过三角形全等进行证明。明确平行四边形的判定定理与相应的性质定理互为逆定理。
    提问学生：求证四边形ABCD是平行四边形，说一说有哪些证明方法?
    预设：可以利用定义，或证明两组对边分别相等，或两组对角分别相等。
    继续提问：思考两组对边分别平行或相等的四边形是平行四边形，如果只考虑四边形的一组对边，它们满足什么条件时这个四边形能成为平行四边形呢?
    学生活动：组织学生前后桌四人一组进行讨论，教师巡视指导。引导学生猜想一组对边平行且相等的四边形是平行四边形，并进行证明。
    通过充分讨论和分享，结合学生的回答，教师明确：平行四边形判定的另一种方法，即一组对边平行且相等的四边形是平行四边形。
    提问学生：现在你有多少种判定一个四边形是平行四边形的方法?
    引导学生回顾平行四边形判定的四种方法。
    (三)课堂练习
    基础题：练习题1，引导学生利用平行四边形判定的四种方法进行证明。
    提升题：练习题2，解决生活实际问题。
    (四)小结作业
    提问：今天有什么收获?
    引导学生回顾：本节课学习了平行四边形判定的四种方法。
    课后梯度作业：必做题和选做题。
    【板书设计】



    1.平行四边形的判定定理都有哪些?
    2.为什么要学习平行四边形的判定?


    答案：
    解析：
    1.
    两组对边分别平行的四边形是平行四边形;两组对边分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形。
    2.
    平行四边形的判定是对前面所学全等三角形和平行四边形性质的一个回顾和延伸，又是后续学习特殊的平行四边形的基础，同时它还进一步培养学生的简单的推理能力、图形迁移能力、观察能力、合情推理能力，使学生学会将平行四边形的问题转化为三角形的问题，渗透化归思想。

  • 第10题：

    在学习了平行四边形、三角形的中位线定理后，某老师设计了一个教学目标。

    ① 进一步理解三角形中位线定理和平行四边形判定定理

    ② 运用三角形中位线定理、平行四边形判定定理解决问题

    ③ 提高发现解决能力

    他的教学过程设计包含以下一道例题：如图1，在四边形ABCD中，EFGH分别是AB、BC、CD、DA中点，

    问题一、求证四边形EFGH是平行四边形。

    问题二、如何改变问题条件，从而分别得到菱形、矩形、正方形。

    针对上述材料，完成以下任务

    （1）结合目标分析该例题设计意图（10分）

    （2）类比上述例题问题二设计一个新问题，使之符合教学目标③要求(8分)

    （3）设计该例题简要教学流程（8分）并给出解题的小结提纲（4分）


    答案：
    解析：
    本题主要考查教学设计相关内容。

  • 第11题：

    下列说法中，不正确的是（　　）。

    A.两组对边分别相等的四边形是平行四边形
    B.平行四边形的对角线互相平分
    C.平行四边形的对边相等
    D.对角线相等的四边形是平行四边形

    答案：D
    解析：
    对于A项，两组对边分别相等的四边形是平行四边形，说法正确；对于B项，平行四边形的对角线互相平分，说法正确；对于C项，平行四边形的对边相等，说法正确；对于D项，对角线相等的四边形是平行四边形，说法错误，例如，等腰梯形对角线相等，但不是平行四边形。故选D。

  • 第12题：

    地形图分幅有（）

    • A、四边形
    • B、梯形分幅
    • C、平行四边形
    • D、矩形分幅

    正确答案:B,D

  • 第13题：

    问答题
    平行四边形面积公式推导的教学片段： （1）教师布置学生独立思考的内容：我们如何把平行四边形转化为已经知道面积公式的平面图形来研究它的面积公式呢？ （2）学生合作交流不到2分钟，当教师发现有一个小组的同学"过平行四边形的一个顶点作平行四边形的高，把平行四边形分割成一个直角三角形和一个直角梯形，然后再等量拼成一个长方形，所以平行四边形的面积就是底乘高"的方法后，就立即宣布合作结束。 从与合作学习有关的因素的角度分析本材料。

    正确答案： 作为新课程倡导的三大学习方式之一，小组合作学习在形式上成为了有别于传统教学的一个最明显特征。它有力地挑战了教师的"一言堂"的专制，在课堂上给了学生自主、合作的机会，当前，很多教师都已经有意识地把它引入课堂，但很多时候的小组合作流于形式。
    在组织小组合作学习前，你可以先回答下列问题：（1）为什么这节课（或者这个环节）要进行小组合作学习？不用可以吗？（2）如果要用，什么时候进行？问题怎么提？大概需要多少时间？可能会出现哪些情况？教师该如何点拔、引导？（3）如何把全班教学、小组教学、个人自学三种具体的教学形式结合起来，做到优势互补？（4）学习中，哪些内容适合进行班级集体教学、哪些内容适合小组合作学习、哪些内容适合个人自学？
    小组合作学习与传统的教学形式不是替代的关系，而是互补的关系。广大的教师在小组合作学习的研究和实践中要有一个科学的态度，不要从一个极端走向另一个极端，从而将传统的教学形式说得一无是处。不讲原则的过多的合作学习也可能限制学生思考的空间，对学生个人能力的发展也是不利的。
    解析： 暂无解析

  • 第14题：

    单选题
    婆罗摩笈多给出的四边形面积公式在只针对（）成立。
    A

    折四边形

    B

    凹四边形

    C

    圆内接四边形

    D

    圆外切四边形


    正确答案： D
    解析： 暂无解析

  • 第15题：

    单选题
    一块四边形荒地，为了防风固沙、保持水土，要在它的四边都种上树，它的四边长分别是120米、144米、192米、168米，要求每两棵树的间隔相等，且四个角都需种树，至少要种多少棵树？（　　）
    A

    24

    B

    26

    C

    28

    D

    30


    正确答案： A
    解析：
    120，144，192，168的最大公约数是24，至少种的棵数为（120＋144＋192＋168）÷24＝26棵。

  • 第16题：

    单选题
    一个四边形的广场它的四边分别是60米、72米、96米、84米，现在要在四边上植树，如果四边上每两棵树的间隔距离相等，那么至少要种多少棵树（）
    A

    20

    B

    22

    C

    24

    D

    26


    正确答案： B
    解析： 暂无解析

相关内容