随机变量X的数学期望E（X）=2，方差D（X）=4，则E（X2）=（）

题目

随机变量X的数学期望E（X）=2，方差D（X）=4，则E（X2）=（）

相似考题

1.X为随机变量,E[X]为其期望,则下面有关X的期望,正确的是:()A E[2X]=2XB E[2X]=2E[X]C E[2X]=2+XD E[2+X]=2X

2.设X服从λ=2的泊松分布,则x的数学期望和方差分别是多少?

3.设随机变量x的分布函数为则数学期望E（X）等于（　　）。

4.设随机变量X的数学期望EX = 1,且满足P{|X－1|>=2}=1／16,根据切比雪夫不等式,X的方差必满足()A.DX>=1/4B.DX>=1/2C.DX>=1/16D.DX>=1

参考答案和解析
正确答案:8
更多“随机变量X的数学期望E（X）=2，方差D（X）=4，则E（X<s”相关问题

  • 第1题：

    设X1,X2,…,Xn,…相互独立,则X1,X2,…,Xn,…满足辛钦大数定律的条件是( )




    A.X1,X2,…,Xn,…同分布且有相同的数学期望与方差
    B.X1,X2,…,Xn,…同分布且有相同的数学期望
    C.X1,X2,…,Xn,…为同分布的离散型随机变量
    D.X1,X2,…,Xn,…为同分布的连续型随机变量

    答案：B
    解析：
    根据辛钦大数定律的条件，应选(B).

  • 第2题：

    已知离散型随机变量X的概率分布为

    (1)求常数a；
    (2)求X的数学期望EX及方差DX．


    答案：
    解析：
    (1)因为0．2+a+0．2+0．3=1，所以a=0．3．(4分)(2)E=0×0．2+10×0．3+20×0．2+30×0．3=16，(7分)
    DX=(0-16)2×0．2+(10-16)2×0．3+(20-16)2×0．2+(30-16)2×0．3=124．(10分)

  • 第3题：

    设离散型随机变量x的分布列为

    ①求常数a的值；
    ②求X的数学期望E(X)．


    答案：
    解析：
    ①随机变量的分布列必须满足规范性，所以0．2+a+0．5=1，得a=0．3．②E(X)=1×0．2+2×0．3+3×0．5=2．3．

  • 第4题：

    设随机变量X的数学期望和方差分别为E(X)=μ,D(x)=σ^2,用切比雪夫不等式估计P{｜X一μ｜<3σ）.


    答案：
    解析：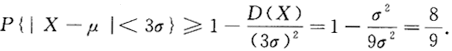

  • 第5题：

    设随机变量x的概率密度为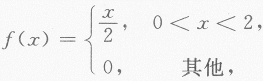F(x)为X的分布函数，EX为X的数学期望，则P{F(X)>EX-1}=________.


    答案：
    解析：

  • 第6题：

    若随机变量Y是X的线性函数，Y=aX+b（a﹥0）且随机变量X存在数学期望与方差，则X与Y的相关系数ρXY=（）

    • A、a
    • B、a2
    • C、0
    • D、1

    正确答案:D

  • 第7题：

    若随机变量X服从参数为n和p的二项分布，则它的数学期望为（），方差是（）


    正确答案:np；npq

  • 第8题：

    已知随机变量X~N（0， 9），那么该随机变量X的期望为（），方差为（）


    正确答案:0；9

  • 第9题：

    设随机变量X与Y相互独立，它们分别服从参数λ=2的泊松分布与指数分布．记Z=X-2Y，则随机变量Z的数学期望与方差分别等于（）．

    • A、1，3
    • B、-2，4
    • C、1，4
    • D、-2，6

    正确答案:A

  • 第10题：

    设随机变量X和Y的数学期望分别为-2和2，方差分别为1和4，而相关系数为-0.5，则根据切比雪夫不等式P{|X+Y|≥6}≤（）。


    正确答案:1/12

  • 第11题：

    多选题
    数学期望的性质包括（）
    A

    设c为常数，则E（c）＝c

    B

    设X为随机变量，α为常数，则E（αX）＝αE（X）

    C

    设X、y是两个随机变量，则E（X±Y）＝E（X）＋E（Y）

    D

    设X、y是相互独立的随机变量，则E（XY）＝E（X）E（Y）

    E

    设c为常数，则E（c）＝0。


    正确答案： A,B
    解析： 设X、y是相互独立的随机变量，则E（XY）＝E（X）E（Y）。

  • 第12题：

    单选题
    设随机变量X与Y相互独立，它们分别服从参数λ=2的泊松分布与指数分布．记Z=X-2Y，则随机变量Z的数学期望与方差分别等于（）．
    A

    1，3

    B

    -2，4

    C

    1，4

    D

    -2，6


    正确答案： C
    解析： 已知参数λ=2的泊松分布的数学期望与方差分别为 E（X）=2，D（X）=2； 参数λ=2的指数分布的数学期望与方差分别为 E（y）=1/2，D（Y）=1/4． 由数学期望与方差的性质得到 E（Z）=E（X-2Y）=E（X）-2E（Y）=2-2×1/2=1， D（Z）=D（X-2Y）=D（x）+（-2）2D（Y）=2+4×1/4=3. 故选（A）．

  • 第13题：

    已知某个连续型随机变量X的数学期望E(X)=1，则X的概率密度函数不可能是( ).

    A.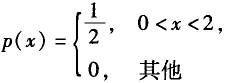
    B.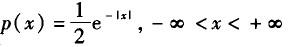
    C.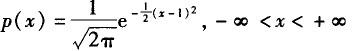
    D.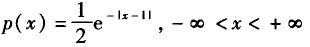

    答案：B
    解析：
    A、C、D的概率密度函数p(x)都关于直线x=1对称，而B的概率密度函数P(x)是偶函数，即关于直线x=0对称.因此，如果数学期望存在，那么B情形下E(X)=0，故选B.

  • 第14题：

    设离散型随机变量X的概率分布为

    求X的数学期望EX及方差DX．


    答案：
    解析：

  • 第15题：

    设随机变量X1,X2,…,Xn相互独立且在［0,na］上服从均匀分布,令U=max{X1,X2,…,Xn},求U的数学期望与方差.


    答案：
    解析：

  • 第16题：

    设随机变量X方差为2,则根据切比雪夫不等式有估计P{｜X-E(X)｜≥2}≤_______.


    答案：
    解析：

  • 第17题：

    设随机变量126X，X，L，X的期望均为0，方差均为1，且任意两个随机变量的相关系数都为1/3，令123Y=X+X+X，456Z=X+X+X，则Y与Z的相关系数为（）。

    • A、1/2
    • B、3/5
    • C、2/3
    • D、5/9
    • E、1/24

    正确答案:B

  • 第18题：

    设随机变量X的数学期望E（X）=75，D（X）=5，且P{|X-75|≥k}≤0.05，则k≥（）。


    正确答案:10

  • 第19题：

    随机变量X的概率分布如：f（X）=X/6X=1，，2，3。则X的数学期望是（）

    • A、0.333
    • B、0.500
    • C、2.000
    • D、2.333

    正确答案:D

  • 第20题：

    设随机变量X和Y的数学期望都是2，方差分别为1和4，而相关系数为0.5，则根据切比雪夫不等式P{|X-Y|≥6}≤（）。


    正确答案:1/12

  • 第21题：

    随机变量X的数学期望EX=μ，方差DX=σ2，k、b为常数，则有E（kX+b）=（）；D（kX+B）=（）。


    正确答案:kμ+b；k2σ2

  • 第22题：

    设随机变量X的方差为2，则P{|X-E（X）|≥2}≤（）。


    正确答案:1/2

  • 第23题：

    单选题
    设随机变量126X，X，L，X的期望均为0，方差均为1，且任意两个随机变量的相关系数都为1/3，令123Y=X+X+X，456Z=X+X+X，则Y与Z的相关系数为（）。
    A

    1/2

    B

    3/5

    C

    2/3

    D

    5/9

    E

    1/24


    正确答案： A
    解析： 暂无解析

相关内容