函数在一点处的左右极限都存在，则函数在这一点的极限存在。

题目

函数在一点处的左右极限都存在，则函数在这一点的极限存在。

相似考题

1.函数在一点处极限存在的充要条件是函数在该点的左极限等于右极限。()此题为判断题(对，错)。

2.设f(x)为连续函数，且下列极限都存在，则其中可推出f′(3)存在的是( )。A. B. C. D.

3.函数y=f(x)在点x=x0处左右极限都存在并且相等，是它在该点有极限的（）A.必要条件 B.充分条件 C.充要条件 D.无关条件

4.若函数f(x)在x0处连续,则f(x)在x0处极限存在。()此题为判断题(对，错)。

更多“函数在一点处的左右极限都存在，则函数在这一点的极限存在。”相关问题

  • 第1题：

    函数y=f（x）在点xo处的左、右极限存在且相等是函数在该点极限存在的（ ）.《》（ ）

    A.必要条件
    B.充分条件
    C.充分必要条件
    D.既非充分条件，也非必要条件

    答案：C
    解析：

  • 第2题：

    设其中g(x)是有界函数，则f(x)在x=0点( )。

    A、极限不存在
    B、极限存在但不连续
    C、连续、但不可导
    D、可导

    答案：D
    解析：

  • 第3题：

    函数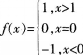x=0点( )。

    A、极限存在，且等于O
    B、左、右极限存在，但极限不存在
    C、左极限存在，但右极限不存在
    D、左极限不存在，但右极限存在

    答案：B
    解析：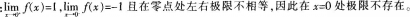

  • 第4题：

    函数在某一点处的导数是一种无穷小比无穷小的极限。


    正确答案:正确

  • 第5题：

    若一点是函数的拐点，则在这点的左右函数的二阶导数要反号。


    正确答案:正确

  • 第6题：

    二元函数的极限与累次极限之间的关系是（）。

    • A、二元函数的极限存在则两累次极限都存在
    • B、累次极限就是二元函数的极限
    • C、两累次极限都存在则二元函数的极限存在
    • D、二元函数的极限和两累次极限都存在时，可用累次极限求二元函数极限

    正确答案:D

  • 第7题：

    若函数φ（z）在复平面内任意一点的导数都存在，则称这个函数在复平面上什么？（）

    • A、解析
    • B、可导
    • C、可分
    • D、可积

    正确答案:A

  • 第8题：

    单选题
    若函数φ（z）在复平面内任意一点的导数都存在，则称这个函数在复平面上什么？（）
    A

    解析

    B

    可导

    C

    可分

    D

    可积


    正确答案： B
    解析： 暂无解析

  • 第9题：

    单选题
    二元函数的极限与累次极限之间的关系是（）。
    A

    二元函数的极限存在则两累次极限都存在

    B

    累次极限就是二元函数的极限

    C

    两累次极限都存在则二元函数的极限存在

    D

    二元函数的极限和两累次极限都存在时，可用累次极限求二元函数极限


    正确答案： A
    解析： 暂无解析

  • 第10题：

    判断题
    若一点是函数的拐点，则在这点的左右函数的二阶导数要反号。
    A

    对

    B

    错


    正确答案： 错
    解析： 暂无解析

  • 第11题：

    单选题
    如果函数f（x）在点x0的某个邻域内恒有|f（x）|≤M（M是正数），则函数f（x）在该邻域内（　　）。
    A

    极限存在

    B

    连续

    C

    有界

    D

    不能确定


    正确答案： C
    解析：
    由函数有界的定义可知：设函数f（x）的定义域为D，数集X∈D。如果存在数K1使得f（x）≤K1对任意x∈X都成立则称函数f（x）在X上有上界。故选C项。

  • 第12题：

    判断题
    函数在一点处的左右极限都存在，则函数在这一点的极限存在。
    A

    对

    B

    错


    正确答案： 错
    解析： 暂无解析

  • 第13题：

    在下列函数中，当x→0时，函数f（x）的极限存在的是《》（ ）


    答案：C
    解析：

  • 第14题：

    函数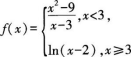在x=3处的极限是( )


    A.不存在

    B.等于6

    C.等于3

    D.等于0

    答案：A
    解析：
    分段函数在x=3处不是无限靠近同一个值，故不存在极限。

  • 第15题：

    设f（x)为不恒等于零的奇函数，且厂(0)存在，则函数()。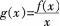

    A、在x=0处左极限不存在
    B、有跳跃间断点x=0
    C、在x=0处右极限不存在
    D、有可去间断点x=0

    答案：D
    解析：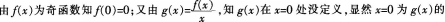

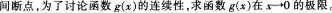
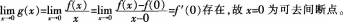
  • 第16题：

    函数在某一点处的导数的几何意义是：函数曲线在这点处的切线。


    正确答案:错误

  • 第17题：

    若x点是函数的可去间断点，则在x点处函数（）。

    • A、左右极限都存在但不相等
    • B、左极限不存在
    • C、左右极限都存在且相等
    • D、右极限不存在

    正确答案:C

  • 第18题：

    若x点是函数的第二类间断点，则在x点处函数（）。

    • A、极限值不等于这点的函数值
    • B、左右极限都存在
    • C、左右极限至少有一个不存在
    • D、没有定义

    正确答案:C

  • 第19题：

    单选题
    若x点是函数的第二类间断点，则在x点处函数（）。
    A

    极限值不等于这点的函数值

    B

    左右极限都存在

    C

    左右极限至少有一个不存在

    D

    没有定义


    正确答案： C
    解析： 暂无解析

  • 第20题：

    单选题
    若x点是函数的可去间断点，则在x点处函数（）。
    A

    左右极限都存在但不相等

    B

    左极限不存在

    C

    左右极限都存在且相等

    D

    右极限不存在


    正确答案： A
    解析： 暂无解析

  • 第21题：

    判断题
    函数在某一点处的导数的几何意义是：函数曲线在这点处的切线。
    A

    对

    B

    错


    正确答案： 错
    解析： 暂无解析

  • 第22题：

    判断题
    函数在某一点处的导数是一种无穷小比无穷小的极限。
    A

    对

    B

    错


    正确答案： 对
    解析： 暂无解析

  • 第23题：

    单选题
    如果函数f（x）当x→x0时极限存在，则函数f（x）在点x0处（　　）。
    A

    有定义

    B

    无定义

    C

    不一定有定义

    D

    连续


    正确答案： C
    解析：
    f（x）当x→x0时极限是否存在与函数在该点有无定义无关，所以A、B两项错误。又该点的极限存在，但不一定连续，且函数f（x）在x0点处连续要求在该点必须有定义，所以D项错误，C项正确。故选C项。

相关内容