函数y=f(x)在点x=x0处左右极限都存在并且相等，是它在该点有极限的（）A.必要条件 B.充分条件 C.充要条件 D.无关条件

题目
函数y=f(x)在点x=x0处左右极限都存在并且相等，是它在该点有极限的（）

A.必要条件
B.充分条件
C.充要条件
D.无关条件
相似考题

1.以下结论正确的是()。A、若x0为函数y=f(x)的驻点,则x0必为函数y=f(x)的极值点.B、函数y=f(x)导数不存在的点,一定不是函数y=f(x)的极值点.C、若函数y=f(x)在x0处取得极值,且f′(x)存在,则必有f′(x)=0.D、若函数y=f(x)在x0处连续,则y=f′(x0)一定存在.

2.若函数f(x)在x0处连续,则f(x)在x0处极限存在。()此题为判断题(对，错)。

3.函数z=f(x，y)在点(x0，y0)处连续是z=f(x，y)在点(x0，y0)处存在一阶偏导数的(58)。A．充分条件B．必要条件C．充要条件D．既非充分，又非必要条件

4.设函数y=f(x)在点x0处可导,且f′(x)0,曲线y=f(x)则在点(x0,f(x0))处的切线的倾斜角为()。A、0B、π/2C、锐角D、钝角

更多“函数y=f(x)在点x=x0处左右极限都存在并且相等，是它在该点有极限的（）”相关问题

  • 第1题：

    f（x）在点x0处的左、右极限存在且相等是f（x）在点x0处连续的（　　）。

    A、 必要非充分的条件
    B、 充分非必要的条件
    C、 充分且必要的条件
    D、 既非充分又非必要的条件

    答案：A
    解析：
    函数f（x）在点x0处连续的充要条件为：在该点处的左右极限存在且相等，并等于函数在该点处的函数值，即：



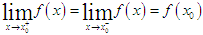
    故f（x）在点x0处的左、右极限存在且相等，并不能得出f（x）在点x0处连续，也可能是可去间断点，为必要非充分条件。

  • 第2题：

    函数y=f(x) 在点x=x0处取得极小值，则必有：
    A. f'(x0)=0
    B.f''(x0)＞0
    C. f'(x0)=0且f''(x0)＞0
    D.f'(x0)=0或导数不存在


    答案：D
    解析：
    提示：已知y=f(x)在x=x0处取得极小值，但在题中f(x)是否具有一阶、二阶导数，均未说明，从而答案A、B、C就不一定成立。答案D包含了在x=x0可导或不可导两种情况，如y= x 在x=0处导数不存在，但函数y= x 在x=0取得极小值。

  • 第3题：

    下列命题正确的是（）

    A.函数f(x)的导数不存在的点，一定不是f(x)的极值点
    B.若x0为函数f(x)的驻点，则x0必为f(x)的极值点
    C.若函数f(x)在点x0处有极值，且f'(x0)存在，则必有f'(x0)＝0
    D.若函数f(x)在点x0处连续，则f'(x0)一定存在

    答案：C
    解析：
    根据函数在点x0处取极值的必要条件的定理，可知选项C是正确的．

  • 第4题：

    对于二元函数z=f（x，y），在点（x0，y0）处连续是它在该点处偏导数存在的什么条件（）？

    • A、必要条件而非充分条件
    • B、充分条件而非必要条件
    • C、充分必要条件
    • D、既非充分又非必要条件

    正确答案:D

  • 第5题：

    下列结论不正确的是（）。

    • A、z=f（x，y）在点（x0，y0）处可微，则f（x，y）在点（x0，y0）处连续
    • B、z=f（x，y）在点（x0，y0）处可微，则f（x，y）在点（x0，y0）处可导
    • C、z=f（x，y）在点（x0，y0）处可导，则f（x，y）在点（x0，y0）处可微
    • D、z=f（x，y）在点（x0，y0）处偏导数连续，则f（x，y）在点（x0，y0）处连续

    正确答案:C

  • 第6题：

    若x点是函数的第二类间断点，则在x点处函数（）。

    • A、极限值不等于这点的函数值
    • B、左右极限都存在
    • C、左右极限至少有一个不存在
    • D、没有定义

    正确答案:C

  • 第7题：

    下列结论不正确的是（）。

    • A、y=f（x）在点x0处可微，则f（x）在点x0处连续
    • B、y=f（x）在点x0处可微，则f（x）在点x0处可导
    • C、y=f（x）在点x0处连续，则f（x）在点x0处可微
    • D、y=f（x）在点x0处可导，则f（x）在点x0处连续

    正确答案:C

  • 第8题：

    单选题
    以下关于二元函数的连续性的说法正确是（　　）。
    A

    若f（x，y）沿任意直线y＝kx在点x＝0处连续，则f（x，y）在（0，0）点连续

    B

    若f（x，y）在点（x0，y0）点连续，则f（x0，y）在y0点连续，f（x，y0）在x0点连续

    C

    若f（x，y）在点（x0，y0）点处偏导数fx′（x0，y0）及fy′（x0，y0）存在，则f（x，y）在（x0，y0）处连续

    D

    以上说法都不对


    正确答案： C
    解析：
    根据二元函数f（x，y）在（x0，y0）出连续的定义可知B项正确。

  • 第9题：

    单选题
    对于二元函数z=f（x，y），在点（x0，y0）处连续是它在该点处偏导数存在的什么条件（）？
    A

    必要条件而非充分条件

    B

    充分条件而非必要条件

    C

    充分必要条件

    D

    既非充分又非必要条件


    正确答案： B
    解析： 暂无解析

  • 第10题：

    判断题
    若连续函数y=f（x）在x0点不可导，则曲线y=f(x)在（x0,f(x0））点没有切线.
    A

    对

    B

    错


    正确答案： 错
    解析： 暂无解析

  • 第11题：

    单选题
    如果函数f（x）在点x0的某个邻域内恒有|f（x）|≤M（M是正数），则函数f（x）在该邻域内（　　）。
    A

    极限存在

    B

    连续

    C

    有界

    D

    不能确定


    正确答案： C
    解析：
    由函数有界的定义可知：设函数f（x）的定义域为D，数集X∈D。如果存在数K1使得f（x）≤K1对任意x∈X都成立则称函数f（x）在X上有上界。故选C项。

  • 第12题：

    判断题
    函数在一点处的左右极限都存在，则函数在这一点的极限存在。
    A

    对

    B

    错


    正确答案： 错
    解析： 暂无解析

  • 第13题：

    函数y=f(x)在点x=x0处取得极小值，则必有：

    A.f′(x0)=0
    B.f′′(x0)＞0
    C. f′(x0)=0 且 f(xo)＞0
    D.f′(x0)=0 或导数不存在

    答案：D
    解析：
    已知y=f(x)在x=x0处取得极小值，但在题中f(x)是否具有一阶、二阶导数，均未说明，从而答案A、B、C就不一定成立。答案D包含了在x=x0可导或不可导两种情况，如 ：y= x 在x=0处导数不存在，但函数y= x 在x=0取得极小值。

  • 第14题：

    函数y = f (x)在点x = x0,处取得极小值，则必有：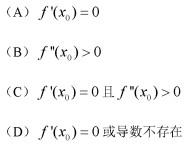


    答案：D
    解析：
    取得极值，有可能是导数不存在，如函数y = x 在x = 0时取得极小值，但在x = 0处导数不存在。

  • 第15题：

    函数y=f（x）在点xo处的左、右极限存在且相等是函数在该点极限存在的（ ）.《》（ ）

    A.必要条件
    B.充分条件
    C.充分必要条件
    D.既非充分条件，也非必要条件

    答案：C
    解析：

  • 第16题：

    若连续函数y=f（x）在x0点不可导，则曲线y=f(x)在（x0,f(x0））点没有切线.


    正确答案:错误

  • 第17题：

    若x点是函数的可去间断点，则在x点处函数（）。

    • A、左右极限都存在但不相等
    • B、左极限不存在
    • C、左右极限都存在且相等
    • D、右极限不存在

    正确答案:C

  • 第18题：

    函数在一点处的左右极限都存在，则函数在这一点的极限存在。


    正确答案:错误

  • 第19题：

    单选题
    若x点是函数的第二类间断点，则在x点处函数（）。
    A

    极限值不等于这点的函数值

    B

    左右极限都存在

    C

    左右极限至少有一个不存在

    D

    没有定义


    正确答案： C
    解析： 暂无解析

  • 第20题：

    单选题
    若x点是函数的可去间断点，则在x点处函数（）。
    A

    左右极限都存在但不相等

    B

    左极限不存在

    C

    左右极限都存在且相等

    D

    右极限不存在


    正确答案： A
    解析： 暂无解析

  • 第21题：

    单选题
    考虑二元函数f（x，y）的下面4条性质：①f（x，y）在点（x0，y0）处连续；②f（x，y）在点（x0，y0）处的两个偏导数连续；③f（x，y）在点（x0，y0）处可微；④f（x，y）在点（x0，y0）处的两个偏导数存在。若用“P⇒Q”表示可由性质P推出Q，则有（　　）。
    A

    ②⇒③⇒①

    B

    ③⇒②⇒①

    C

    ③⇒④⇒①

    D

    ③⇒①⇒④


    正确答案： C
    解析：
    根据二元函数连续、可微及可导的关系可知②⇒③⇒①、②⇒③⇒④。

  • 第22题：

    单选题
    二元函数z＝f（x，y）在点（x0，y0）处存在一阶连续偏导数是它在此点处可微的（　　）。
    A

    充分条件

    B

    必要条件

    C

    充要条件

    D

    以上都不是


    正确答案： C
    解析：
    一阶偏导数在（x0，y0）点连续，则函数在（x0，y0）处可微；而函数在（x0，y0）处可微，其一阶偏导数不一定连续。

  • 第23题：

    单选题
    如果函数f（x）当x→x0时极限存在，则函数f（x）在点x0处（　　）。
    A

    有定义

    B

    无定义

    C

    不一定有定义

    D

    连续


    正确答案： C
    解析：
    f（x）当x→x0时极限是否存在与函数在该点有无定义无关，所以A、B两项错误。又该点的极限存在，但不一定连续，且函数f（x）在x0点处连续要求在该点必须有定义，所以D项错误，C项正确。故选C项。

相关内容