单选题由1、2、3组成没有重复数字的所有三位数之和是多少？（）A 1222B 1232C 1322D 1332

题目
单选题
由1、2、3组成没有重复数字的所有三位数之和是多少？（）
A

1222

B

1232

C

1322

D

1332

相似考题

1.从1，2，3，4，5中任取3个数，组成的没有重复数字的三位数共有 （ ）A.40个B.80个C.30个D.60个

2.（10）由1、2、3、4、5、6组成没有重复数字且1、3都不与5相邻的六位偶数的个数是（A）72（B）96（C） 108（D）144

3.（9）由1、2、3、4、5 组成没有重复数字且1、2 都不与5 相邻的五位数的个数是（A）36（B）32（C）28（D）24

4.（16）用数字0，1，2，3，4，5，6组成没有重复数字的四位数，其中个位、十位和百位上的数字之和为偶数的四位数共有 个（用数字作答）

更多“由1、2、3组成没有重复数字的所有三位数之和是多少？（）”相关问题

  • 第1题：

    用0，1，2，…，9这十个数字，可以组成没有重复数字的三位数的个数为

    A．720

    B．648

    C．620

    D．548


    正确答案：B

  • 第2题：

    一个三位数的各位数字之和是16，其中十位数字比个位数字小3。如果把这个三位数的百位数字与个位数字对调，得到一个新的三位数，则新的三位数比原三位数大495，则原来的三位数是多少?

    A．169

    B．358

    C．469

    D．736


    正确答案：B
    此题用排除法。由“各位数字之和是16”可排除C项；由“百位数字与个位数字对调，得到一个新的三位数，则新的三位数比原三位数大495”可排除选项A、D两项，故此题选B。

  • 第3题：

    由1、2、3组成没有重复数字的所有三位数之和是多少？

    A．1222

    B．1232

    C．1322

    D．1332


    正确答案：D

  • 第4题：

    由1、2、3组成没有重复数字的所有三位数之和是多少?（ ） A．1 222 B．1 232 C．1 322 D．1 332


    正确答案：D
    观察四个备选答案可知，本题无法用尾数法进行排除，所以只能逐一列出后进行运算。123＋132+213+231+312+321=1332。故选D。

  • 第5题：

    由1，2，3，4，5这5个数字组成的没有重复数字的五位数中，有多少个大于34152?（）

    A. 50
    B. 54
    C. 58
    D. 60

    答案：C
    解析：
    由题知，满足题意的五位数分为以下几种情况：
    (1)万位数是5的五位数共有4X3X2Xl = 24（个）；
    (2)万位数是4的五位数共有4X3X2X1 = 24（个）；
    (3)万位数是3，则千位数只能是5或4。千位数是5时共有3X2X1 = 6（个）五位数满足题意；千位数是4的满足题意的五位数共有如下4个：34215，34251，34512，34521。
    所以，共有24 + 24 + 6 + 4 = 58 （个）数大于34152。本题正确答案为C。

  • 第6题：

    从1、2、3、4中任取3个数组成没有重复的三位数的偶数，取法种数为（）。

    A.13
    B.12
    C.10
    D.11

    答案：B
    解析：
    题干要求组成没有重复数字的三位数的偶数，只有尾数是2或4两种情况。当尾数是2时，有2x3=6(种）；当尾数是4时，有2x3=6(种），所以共有6+6=12(种），故本题答案为B。

  • 第7题：

    由1、2、3组成的没有重复数字的所有三位数之和为多少?( )


    A. 1222
    B. 1232
    C. 1322
    D. 1332

    答案：D
    解析：
    解题指导： 因为1、2、3之和可被3整除，故而1、2、3所组成的没有重复数字的三位数都能被3整除，而这些数字相加之和也必能被3整除，只有D项能被3整除，为正确答案。根据排列组合原理，可知该没有重复数字的三位数共有6个，1、2、3三个数在个、十、百位上各出现两次，即（1+2+3）×2=12，也就是说这一数字当为12+120+1200=1332。故答案为D。

  • 第8题：

    由1，3，5，7，9五个数字组成的没有重复数字的五位数有120个，将它们从小到大排列起来，第50个数是多少？

    A.51739
    B.53197
    C.53179
    D.51397

    答案：D
    解析：
    第一步，本题考查多位数问题。
    第二步，由1，3，5，7，9五个数字组成的没有重复数字的五位数中，以1开头（作为万位）的五位数有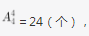

    是120个数中最小的24个；同理，以3开头（作为万位）的五位数也有＝24（个），是120个数中次小的24个；以1和3开头（作为万位）的五位数共有24＋24＝48（个）。
    第三步，从小到大排列起来，第50个数字应该是以5开头（作为万位）中第二小的数字，即51397。（51379是以5为万位最小的数字）。

  • 第9题：

    在1,2,3,4,5这五个数字组成的没有重复数字的三位数中,各位数字之和为奇数的共有（ ）

    A.24个
    B.16个
    C.28个
    D.14个
    E.30个

    答案：A
    解析：

  • 第10题：

    在由数字1，2，3，4，5组成的所有没有重复数字的5位数中，大于23145且小于43521的数共有（）。

    • A、56个
    • B、57个
    • C、58个
    • D、60个

    正确答案:C

  • 第11题：

    由1、2、3组成没有重复数字的所有三位数之和是多少？（）

    • A、1222
    • B、1232
    • C、1322
    • D、1332

    正确答案:D

  • 第12题：

    单选题
    用2，3，4，5，6，7六个数字组成两个三位数，每个数字只用一次，这两个三位数的差最小是多少？（　　）
    A

    47

    B

    49

    C

    69

    D

    111


    正确答案： C
    解析：
    因为每个数字只能用一次，故首位决定大小，三个三位数的百位数字至少相差1，在这种情况下要使差值最小，则两个三位数应为最接近，即较小的三位数之末两位应尽可能大，而较大的三位数之末两位应尽可能小。因此合适的三位数情况构造为523和476，此时三位数之末两位的之末两位的差距最大，故三位数差值最小，为523－476＝47。

  • 第13题：

    由0，1，2，3，4五个数字组成没有重复数字的五位偶数的个数为

    A．120个

    B．60个

    C．36个

    D．24个


    正确答案：B

  • 第14题：

    由1，2，3 组成的没有重复数字的所有三位数之和为多少？（ ）

    A.1222 B.1232 C.1322 D.1332


    正确答案：D

  • 第15题：

    由1、2、3组成的没有重复数字的所有三位数之和为多少?（ ）

    A．1222

    B．1232

    C．1322

    D．1332


    正确答案：D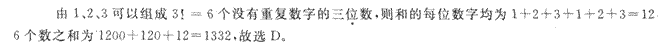

  • 第16题：

    由1、2、3组成的没有重复数字的所有三位数之和为多少？( )

    A．1222

    B．1232

    C. 1322

    D．1332


    正确答案：D
    94.D【解析】对其中任何一个数字，分别有2次出现在个位，所以所有这些数字的个位数字之和是(1+2+3)×2=12，同理所有这些数字的十位、百位数字之和都是12,所以所有这些数字之和是12+ 12×lO十12×100=1332，故选D。

  • 第17题：

    用数字0，1，2，3，4，5可组成无重复数字的三位数个数是（）

    A.120
    B.20
    C.100
    D.10

    答案：C
    解析：

  • 第18题：

    由1、2、3组成没有重复数字的所有三位数之和是多少？

    A. 1222
    B. 1232
    C. 1322
    D. 1332

    答案：D
    解析：
    123+132+213+231+312+321=1332 。故答案为D。

  • 第19题：

    用2、3、4、5、6、7六个数字组成两个三位数，每个数字只用一次，这两个三位数的差最小是多少？（）

    A.47
    B.49
    C.69
    D.111

    答案：A
    解析：
    要使两个三位数的差值最小，百位数必须相邻，十位数必须差距最大，所以较大数上的十位数为2，较小数上的十位数为7，个位上剩下3,4，5，6，则较小数上的个位数为3，较小数上的个位为6，故较大数为523，较小数为476，相减得差为47。

  • 第20题：

    由数字1、2、3、4、5、6可组成多少个没有重复数字的四位奇数?( )

    A.15
    B.180
    C.720
    D.4096

    答案：B
    解析：
    根据题意可知，个位数必须用奇数，有3种选择，则总共有3XA53=3×5×4x3=180个。故选B。

  • 第21题：

    从1、2、3、4中任取3个数组成没有重复的三位数且必须为偶数，则取法种数为（ ）。
    A. 13 B. 12 C. 10 D. 11


    答案：B
    解析：
    题干要求组成没有重复数字的三位数且是偶数，只有尾数是2或4两种情况。当尾数是2时，有2X3 = 6（种）；当尾数是4时，有2X3 = 6（种），所以共有6 + 6 = 12（种），故本题答案为B。

  • 第22题：

    由1、3、6可以组成几个没有重复数字的三位数（）

    • A、4.0
    • B、5.0
    • C、6.0
    • D、7.0

    正确答案:C

  • 第23题：

    问答题
    桌子上有3张数字卡片，这几张卡片组成三位数字236。如果把这3张卡片变换一下位置或方向，就会组成另外一个三位数，而且这个三位数恰好能够被47整除。那么如何改变卡片的方位呢？这个三位数是多少呢？

    正确答案： 能够被47整除的三位数有94，141，188，235，282，329……要仔细得观察236这个数字，看怎么变动可以满足要求。可以将236中的23左右交换为32，再把6的那张卡片上下倒置变为“9”即可变为“329”，能够被47整除。
    解析： 暂无解析

  • 第24题：

    单选题
    在由数字1，2，3，4，5组成的所有没有重复数字的5位数中，大于23145且小于43521的数共有（）。
    A

    56个

    B

    57个

    C

    58个

    D

    60个


    正确答案： A
    解析： 暂无解析

相关内容