(9)由1、2、3、4、5 组成没有重复数字且1、2 都不与5 相邻的五位数的个数是(A)36(B)32(C)28(D)24
题目
(9)由1、2、3、4、5 组成没有重复数字且1、2 都不与5 相邻的五位数的个数是
(A)36
(B)32
(C)28
(D)24
相似考题
参考答案和解析
正确答案:A
更多“(9)由1、2、3、4、5 组成没有重复数字且1、2 都不与5 相邻的五位数的个数是(A)36 (B)32 (C)28 (D)24 ”相关问题
-
第1题:
1、2、3、4、5、6这七个数字能够组成多少个被125整除的无重复数字的五位数? A.9 B.12 C.21 D.24
正确答案:C
能被125整除,则五位数的后三位应该是125或者250。如果后三位数是125,则有3×3=9个数;如果后三位数是250,则有4×3=12个数。
故一共可以组成9+12=21个被125整除的五位数。
-
第2题:
从0,2,4,6中取出3个数字,从1,3,5,7中取出两个数字,共能组成多少个没有重复数字且大于65000的五位数答案:解析:根据约束条件“大于65000的五位数”可知这样的五位数只有 7××××、65×××、67×××三种类型.
(1)能组成7××××型的五位数的个数是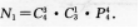
(2)能组成65×××型的五位数的个数是
(3)能组成67×××型的五位数的个数是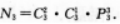
故所求的五位数的个数为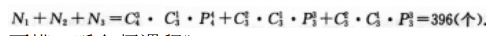
-
第3题:
用数字0,1,2,3,4,5可以组成没有重复数字,并且比20000大的五位数共有 个.
(1) (2) (3) 略 -
第4题:
由1,2,3,4,5这5个数字组成的没有重复数字的五位数中,有多少个大于34152?()A. 50
B. 54
C. 58
D. 60答案:C解析:由题知,满足题意的五位数分为以下几种情况:
(1)万位数是5的五位数共有4X3X2Xl = 24(个);
(2)万位数是4的五位数共有4X3X2X1 = 24(个);
(3)万位数是3,则千位数只能是5或4。千位数是5时共有3X2X1 = 6(个)五位数满足题意;千位数是4的满足题意的五位数共有如下4个:34215,34251,34512,34521。
所以,共有24 + 24 + 6 + 4 = 58 (个)数大于34152。本题正确答案为C。 -
第5题:
由1,2,3,4,5构成的无重复数字的五位数中,大于34000的五位数有( )个A.36
B.48
C.60
D.72
E.90答案:C解析:
