单选题设f（x）在（－∞，＋∞）内可导，且对任意x2＞x1，都有f（x2）＞f（x1），则正确的结论是（　　）。A 对任意x，f′（x）＞0B 对任意x，f′（x）≤0C 函数－f（－x）单调增加D 函数f（－x）单调增加

题目
单选题
设f（x）在（－∞，＋∞）内可导，且对任意x2＞x1，都有f（x2）＞f（x1），则正确的结论是（　　）。
A

对任意x，f′（x）＞0

B

对任意x，f′（x）≤0

C

函数－f（－x）单调增加

D

函数f（－x）单调增加

相似考题

1.已知x1(t)和x2(t)的傅里叶变换分别为X1(f)和X2(f),则卷积x1(t)*x2(t)的傅里叶变换为()。A、X1(f)X2(f)B、X1(f)*X2(f)C、X1(-f)X2(-f)D、X1(-f)*X2(-f)

2.A.对任意x，f′（x）＞0 B.对任意x，f′（x）≤0 C.函数-f（-x）单调增加 D.函数f（-x）单调增加

3.下列命题中，正确的是( ).A.单调函数的导函数必定为单调函数 B.设f´(x)为单调函数，则f(x)也为单调函数 C.设f(x)在(a，b)内只有一个驻点xo，则此xo必为f(x)的极值点 D.设f(x)在(a，b)内可导且只有一个极值点xo，f´(xo)=0

4.已知函数f(x)=(a+1)lnx+ax2+1.(Ⅰ)讨论函数f(x)的单调性；(Ⅱ)设a≤-2，证明：对任意x2,x2 (0,+∞)，|f(x1)-f(x2)|≥4|x1-x2|.

更多“单选题设f（x）在（－∞，＋∞）内可导，且对任意x2＞x1，都有f（x2）＞f（x1），则正确的结论是（　　）。A 对任意x，f′（x）＞0B 对任意x，f′（x）≤0C 函数－f（－x）单调增加D 函数f（－x）单调增加”相关问题

  • 第1题：

    设随机变量X的密度函数为f(x),且f(x)为偶函数,X的分布函数为F(x),则对任意实数a,有().



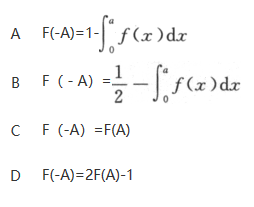    答案：B
    解析：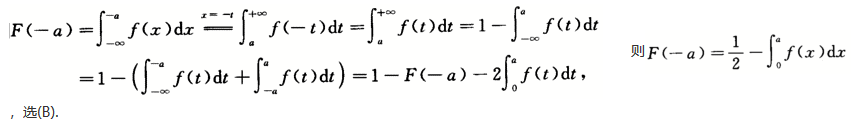

  • 第2题：

    设随机变量X的密度函数为f(x)，且f(-x)=f(x)，F(x)是X的分布函数，则对任意实数a有( )。

    A.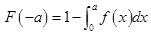
    B.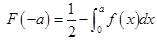
    C.F(-a)=F(a)
    D.F(-a)=2F(a)-1

    答案：B
    解析：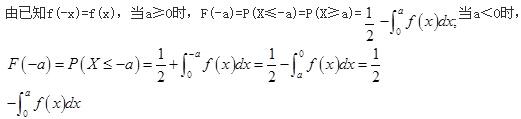

  • 第3题：

    设随机变量x的密度函数为f(x)，且f(-x)=f（x)，F(x)是X的分布函数，则对任意实数 a，有( )。


    答案：B
    解析：

  • 第4题：

    设f(x)处处连续，且在x=x1处有f'(x1)=0,在x=x2处不可导，那么（ ）。
    A.x=x1及x=x2都必不是f(x)的极值点
    B.只有x=x1是f(x)的极值点
    C.x=x1及x=x2都有可能是f(x)的极值点
    D.只有x=x2是f(x)的极值点


    答案：C
    解析：
    提示：驻点和导数不存在点都是极值可疑点。

  • 第5题：

    已知函数



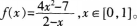
    (1)求f(x)单调区间与值域；
    (2)设a≥1，函数g(x)=x3-3a2x-2a，x∈[0，1]。若对于任意x1∈[0，1]，总存在x0∈[0，1]使g(x0)=f(x1)成立，求a的取值范围。



    答案：
    解析：

  • 第6题：

    F（x）为随机变量的分布函数，当x2>x1时，有F（x2）（）F（x1）。


    正确答案:≥

  • 第7题：

    已知函数定义Functionf（x1%，x2%）as integer，则下列调用语句正确的是（）

    • A、a=f（x，y）
    • B、call f（x，y）
    • C、f（x，y）
    • D、fxy

    正确答案:A

  • 第8题：

    设函数f（x）在（-∞，+∞）上是偶函数，且在（0，+∞）内有f＇（x）>0，f＂（x）>0，则在（-∞，0）内必有（）。

    • A、f＇（x）>0，f＂（x）>0
    • B、f＇（x）<0，f＂（x）>0
    • C、f＇（x）>O，f＂（x）<0
    • D、f＇（x）<0，f＂（x）<0

    正确答案:B

  • 第9题：

    单选题
    设f（x）处处连续，且在x=x1处有f＇（x1）=0，在x=x2处不可导，那么（）。
    A

    x=x1及x=x2都必不是f（x）的极值点

    B

    只有x=x1是f（x）的极值点

    C

    x=x1及x=x2都有可能是f（x）的极值点

    D

    只有x=x2是f（x）的极值点


    正确答案： D
    解析： 暂无解析

  • 第10题：

    问答题
    设f（x）在（a，b）内二阶可导，且f″（x）≥0，证明：对于（a，b）内任意两点x1、x2及0≤t≤1，有f[（1－t）x1＋tx2]≤（1－t）f（x1）＋tf（x2）。

    正确答案：
    由于不等式中含有f[(1-t)x1+tx2]、f(x1)、f(x2),则应在x0=(1-t)x1+tx2处展开泰勒式,即f(x)=f(x0)+f′(x0)(x-x0)+f″(ξ)(x-x0)2/(2!),ξ介于x和x0之间。
    又f″(x)≥0,则f″(ξ)≥0。故f(x)≥f(x0)+f′(x0)(x-x0)。则
    f(x1)≥f(x0)+f′(x0)(x1-x0)①
    f(x2)≥f(x0)+f′(x0)(x2-x0)②
    ①(1-t)+②t,得(1-t)f(x1)+tf(x2)≥f(x0)+f′(x0)[(1-t)x1+tx2-x0]=f(x0),即(1-t)f(x1)+tf(x2)≥f[(1-t)x1+tx2]。
    解析： 暂无解析

  • 第11题：

    单选题
    设函数f（x）={x2，x≤1；ax+b，x>1}，为使函数f（x）在x=1处连续且可导，则（）。
    A

    a=1，b=0

    B

    a=0，b=1

    C

    a=2，b=-1

    D

    a=-1，b=2


    正确答案： A
    解析： 暂无解析

  • 第12题：

    单选题
    映射f：A→B，若A中任意两个不同元素x1≠x2有f（x1）≠f（x2），则f是（）。
    A

    单射

    B

    满射

    C

    双射

    D

    反射


    正确答案： B
    解析： 暂无解析

  • 第13题：

    设f（x）是定义在[-a，a]上的任意函数，则下列答案中哪个函数不是偶函数？

    A.f（x）+f（-x）
    B.f（x）*f（-x）
    C.[f（x）]2
    D.f（x2）

    答案：C
    解析：
    提示：利用函数的奇偶性定义来判定。选项A、B、D均满足定义F（-x）=F（x），所以为偶函数，而C不满足，设F（x）= [f（x）]2，F（-x）= [f（-x）]2，因为f（x）是定义在 [-a,a]上的任意函数，f（x）可以是奇函数，也可以是偶函数，也可以是非奇非偶函数，从而推不出F（-x）=F（x）或 F（-x） = -F（x）。

  • 第14题：

    函数y=f（x）在（a，6）内二阶可导，且f′（x）＞0，f″（x）＜0，则曲线y=f（x）在（a，6）内（ ）.《》（ ）

    A.单调增加且为凹
    B.单调增加且为凸
    C.单调减少且为凹
    D.单调减少且为凸

    答案：B
    解析：
    本题考查的知识点为利用一阶导数符号判定函数的单调性和利用二阶导数符号判定曲线的凹凸性.由于在（a，6）内，f′（x）＞0，可知f（x）在（a，b）内单调增加，又由于，f″（x）＜0，可知曲线y=f（x）在（a，b）内为凸，可知应选B.

  • 第15题：

    二元多项式f（x1,x2)，如果将x1，x2对换后，有f(x1,x2=f(x2,x1)则称f（x1,x2）为二元对称多项式。下列是二元对称多项式的是( )。
    A．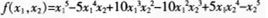
    B．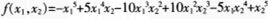
    C．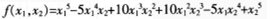
    D．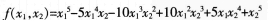


    答案：C
    解析：
    由定义，互换石。，石：的位置，二元多项式不变，即正确选项为选项C。

  • 第16题：

    设函数f(x)在(0，1)内可导，f'(x)>0，则f(x)在(0，1)内（　　）

    A.单调减少
    B.单调增加
    C.为常量
    D.不为常量，也不单调

    答案：B
    解析：
    由于f'(x)>0，可知f(x)在(0，1)内单调增加．因此选B．

  • 第17题：

    设可导函数f（x）满足xf′（x）-f（x）＞0，则（）。

    • A、单调减少
    • B、单调增加
    • C、是常数且为1
    • D、是常数且为2

    正确答案:B

  • 第18题：

    映射f：A→B，若A中任意两个不同元素x1≠x2有f（x1）≠f（x2），则f是（）。

    • A、单射
    • B、满射
    • C、双射
    • D、反射

    正确答案:A

  • 第19题：

    设f（x）处处连续，且在x=x1处有f＇（x1）=0，在x=x2处不可导，那么（）。

    • A、x=x1及x=x2都必不是f（x）的极值点
    • B、只有x=x1是f（x）的极值点
    • C、x=x1及x=x2都有可能是f（x）的极值点
    • D、只有x=x2是f（x）的极值点

    正确答案:C

  • 第20题：

    单选题
    设函数f（x）在区间[1，＋∞）内二阶可导，且满足条件f（1）＝f′（1）＝0，x＞1时f″（x）＜0，则g（x）＝f（x）/x在（1，＋∞）内（　　）。
    A

    曲线是向上凹的

    B

    曲线是向上凸的

    C

    单调减少

    D

    单调增加


    正确答案： A
    解析：
    判断函数的单调性及凹凸性，需求出其导函数和二阶导数，并判断其正负号。g′（x）＝[xf′（x）－f（x）]/x2，构造函数F（x）＝xf′（x）－f（x），F′（x）＝xf″（x）＜0（题中已给出f″（x）＜0），故F（x）单调减少。则F（x）＜F（1）＝0，故g′（x）＜0，即g（x）在（1，＋∞）内单调减少。

  • 第21题：

    单选题
    若函数f（x）在区间（a，b）内可导，x1和x2是区间（a，b）内任意两点（x1＜x2），则至少存在一点ξ，使（　　）
    A

    f（b）－f（a）＝f′（ξ）（b－a）（a＜ξ＜b）

    B

    f（b）－f（x1）＝f′（ξ）（b－x1）（x1＜ξ＜b）

    C

    f（x2）－f（x1）＝f′（ξ）（x2－x1）（x1＜ξ＜x2）

    D

    f（x2）－f（a）＝f′（ξ）（x2－a）（a＜ξ＜x2）


    正确答案： C
    解析：
    考查拉格朗日中值定理的应用。
    值得注意的是，当函数f（x）在[a，b]上连续且在（a，b）内可导时，才可在[a，b]上对函数f（x）应用拉格朗日中值定理。
    由于题中没有说明函数f（x）在[a，b]上连续，因此有可能f（x）在x＝a或x＝b上没有定义，选项中涉及f（a）、f（b）的均为错误选项。

  • 第22题：

    单选题
    设f（x）在（－∞，＋∞）内可导，且对任意x2＞x1，都有f（x2）＞f（x1），则正确的结论是（　　）。
    A

    对任意x，f′（x）＞0

    B

    对任意x，f′（x）≤0

    C

    函数－f（－x）单调增加

    D

    函数f（－x）单调增加


    正确答案： A
    解析：
    令F（x）＝－f（－x），由题知x2＞x1，则－x2＜－x1，则有f（－x2）＜f（－x1），即－f（－x2）＞－f（－x1），即F（x2）＞F（x1）单调增加，C正确。取f（x）＝x3，可排除A项。取f（x）＝x，可排除B、D项。

  • 第23题：

    问答题
    设函数f（x）在（a，b）内连续，a＜x1＜x2＜…＜xn＜b，证明：必∃ξ∈（a，b），使f（ξ）＝[f（x1）＋f（x2）＋…＋f（xn）]/n。

    正确答案：
    设f(x)在[x1,xn]上的最大值为M,最小值为m。
    则由题设可知,f(x)在[x1,xn]上连续,则它在[x1,xn]上必有最大值和最小值,则m≤[f(x1)+f(x2)+…+f(xn)]/n≤M。
    由最值介值定理可知,必∃ξ∈[x1,xn]⊂(a,b),使得f(ξ)=[f(x1)+f(x2)+…+f(xn)]/n。
    解析： 暂无解析

  • 第24题：

    单选题
    设f（x）是定义在［-a，a］上的任意函数，则下列答案中哪个函数不是偶函数？（）
    A

    f（x）+f（-x）

    B

    f（x）·f（-x）

    C

    ［f（x）］2

    D

    f（x2）


    正确答案： A
    解析： 暂无解析

相关内容