已知函数f(x)=(a+1)lnx+ax2+1.(Ⅰ)讨论函数f(x)的单调性；(Ⅱ)设a≤-2，证明：对任意x2,x2 (0,+∞)，|f(x1)-f(x2)|≥4|x1-x2|.

题目

已知函数f(x)=(a+1)lnx+ax2+1.

(Ⅰ)讨论函数f(x)的单调性；

(Ⅱ)设a≤-2，证明：对任意x2,x2 (0,+∞)，|f(x1)-f(x2)|≥4|x1-x2|.

相似考题

1.已知x1(t)和x2(t)的傅里叶变换分别为X1(f)和X2(f),则卷积x1(t)*x2(t)的傅里叶变换为()。A、X1(f)X2(f)B、X1(f)*X2(f)C、X1(-f)X2(-f)D、X1(-f)*X2(-f)

2.设f(x)=3x,g(x)=x2，则函数g[f(x)]-f[g(x)]=_______________.

3.请补充main函数，该函数的功能是求方程ax2+bx+c=0的根(方程的系数a,b,c从键盘输入)。例如， 当a=1，b=2，c=1时， 方程的两个根分别是：x1=-1.00,x2=-1.00。注意：部分源程序给出如下。请勿改动主函数main和其他函数中的任何内容，仅在 main函数的横线上填入所编写的若干表达式或语句。试题程序：include ＜stdio.h＞include ＜conio.h＞include ＜math.h＞main(){float a，b，c，disc，x1，x2，p，q；scanf("%f，%f，%f"，&a，&b，&c)；disc=b*b-4*a*c；clrscr()；printf("****** the result ****+*+\n")；if(disc＞=0){x1=【 】；x2=(-b-sqrt(disc))/(2*a)；printf("x1=%6．2f，x2=%6.2f\n"，x1，x2)；}else{p=【 】；q=【 】；printf("x1=%6.2f+%6.2f i\n"，p，q)；printf("x2=%6.2f-%6.2f i\n"，p，q)；}}

4.设x2为f(x)的一个原函数，则f(x)=_______

参考答案和解析
正确答案：


更多“已知函数f(x)=(a＋1)lnx＋ax2＋1. (Ⅰ)讨论函数f(x)的单调性; (Ⅱ)设a≤－2,证明:对任意x2,x2 ”相关问题

  • 第1题：

    设f（x）是定义在[-a，a]上的任意函数，则下列答案中哪个函数不是偶函数？

    A.f（x）+f（-x）
    B.f（x）*f（-x）
    C.[f（x）]2
    D.f（x2）

    答案：C
    解析：
    提示：利用函数的奇偶性定义来判定。选项A、B、D均满足定义F（-x）=F（x），所以为偶函数，而C不满足，设F（x）= [f（x）]2，F（-x）= [f（-x）]2，因为f（x）是定义在 [-a,a]上的任意函数，f（x）可以是奇函数，也可以是偶函数，也可以是非奇非偶函数，从而推不出F（-x）=F（x）或 F（-x） = -F（x）。

  • 第2题：

    设f(x)是连续函数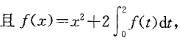， 则f(x)=
    A. x2 B. x2-2 C 2x D. x2 -16/9


    答案：D
    解析：

  • 第3题：

    设f(x)是连续函数，
    　　(Ⅰ)利用定义证明函数可导，且F’(x)=f(x)；
    　　(Ⅱ)当f(x)是以2为周期的周期函数时，证明函数也是以2为周期的周期函数.


    答案：
    解析：



  • 第4题：

    求函数．f(x)＝x2?2x在x=0处的n阶导数,f(n)(O)。


    答案：
    解析：
    函数乘积求高阶导数，莱布尼茨公式。

  • 第5题：

    设f(x)是连续函数，且，则f(x)=( )。
    A. x2 B. X2-2 C. 2x D. x2-16/9


    答案：D
    解析：

  • 第6题：

    设f（x）的一个原函数为cosx，g（x）的一个原函数为x2，则f［g（x）］等于：（）

    • A、cosx2
    • B、-sinx2
    • C、cos2x
    • D、-sin2x

    正确答案:D

  • 第7题：

    已知函数定义Functionf（x1%，x2%）as integer，则下列调用语句正确的是（）

    • A、a=f（x，y）
    • B、call f（x，y）
    • C、f（x，y）
    • D、fxy

    正确答案:A

  • 第8题：

    单选题
    设f（x）的一个原函数为cosx，g（x）的一个原函数为x2，则f［g（x）］等于：（）
    A

    cosx2

    B

    -sinx2

    C

    cos2x

    D

    -sin2x


    正确答案： A
    解析： 利用原函数定义，求出f（x）、g（x）；利用复合函数关系求出f[g（x）]。

  • 第9题：

    单选题
    设f（x）是定义在［-a，a］上的任意函数，则下列答案中哪个函数不是偶函数？（）
    A

    f（x）+f（-x）

    B

    f（x）·f（-x）

    C

    ［f（x）］2

    D

    f（x2）


    正确答案： B
    解析： 暂无解析

  • 第10题：

    单选题
    设f（x）在（－∞，＋∞）内可导，且对任意x2＞x1，都有f（x2）＞f（x1），则正确的结论是（　　）。
    A

    对任意x，f′（x）＞0

    B

    对任意x，f′（x）≤0

    C

    函数－f（－x）单调增加

    D

    函数f（－x）单调增加


    正确答案： A
    解析：
    令F（x）＝－f（－x），由题知x2＞x1，则－x2＜－x1，则有f（－x2）＜f（－x1），即－f（－x2）＞－f（－x1），即F（x2）＞F（x1）单调增加，C正确。取f（x）＝x3，可排除A项。取f（x）＝x，可排除B、D项。

  • 第11题：

    问答题
    设函数f（x）在（a，b）内连续，a＜x1＜x2＜…＜xn＜b，证明：必∃ξ∈（a，b），使f（ξ）＝[f（x1）＋f（x2）＋…＋f（xn）]/n。

    正确答案：
    设f(x)在[x1,xn]上的最大值为M,最小值为m。
    则由题设可知,f(x)在[x1,xn]上连续,则它在[x1,xn]上必有最大值和最小值,则m≤[f(x1)+f(x2)+…+f(xn)]/n≤M。
    由最值介值定理可知,必∃ξ∈[x1,xn]⊂(a,b),使得f(ξ)=[f(x1)+f(x2)+…+f(xn)]/n。
    解析： 暂无解析

  • 第12题：

    问答题
    10.设F1(x)，F2(x)分别为随机变量X1和X2的分布函数，且F(x)=aF1(x)一bF2(x)也是某一随机变量的分布函数，证明a—b=1．

    正确答案：
    解析：

  • 第13题：

    设F1(x)与F2(x)分别为随机变量X1与X2的分布函数。为使F(x)=aF1(x)-bF2(x)成为某一随机变量的分布函数，则a与b分别是：


    答案：A
    解析：

  • 第14题：

    设X～N（μ,σ^2）,其分布函数为F(x),对任意实数a,讨论F(-a)+F(a)与1的大小关系.


    答案：
    解析：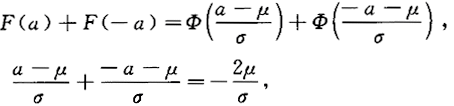

    则μ>0时，F(a)+F（-a）小于1；
    当μ=0时，F(a)+F（-a）=1；
    当μa小于0时，F(a)+F（-a）大于1.

  • 第15题：

    设函数f(x)＝ex，则．f(x－a)·f(x＋a)＝（　　）

    A.f(x2－a2)
    B.2f(x)
    C.f(x2)
    D.f2(x)

    答案：D
    解析：

  • 第16题：

    已知 X1 和 X2 是相互独立的随机变量，分布函数分别为F1（x）和F2（x），则下列选项一定是某一随机变量分布函数的为（ ）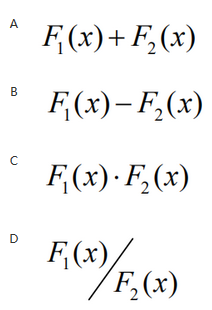


    答案：C
    解析：
    分布函数要满足非负性，规范性，单调不减性，右连续性.

  • 第17题：

    F（x）为随机变量的分布函数，当x2>x1时，有F（x2）（）F（x1）。


    正确答案:≥

  • 第18题：

    F（x）为随机变量的分布函数，当x2>x1时，有F（x2）（）F（x1）.

    • A、>
    • B、≥
    • C、<
    • D、≤

    正确答案:B

  • 第19题：

    单选题
    已知函数定义Functionf（x1%，x2%）as integer，则下列调用语句正确的是（）
    A

    a=f（x，y）

    B

    call f（x，y）

    C

    f（x，y）

    D

    fxy


    正确答案： B
    解析： 暂无解析

  • 第20题：

    单选题
    若函数f（x）在区间（a，b）内可导，x1和x2是区间（a，b）内任意两点（x1＜x2），则至少存在一点ξ，使（　　）
    A

    f（b）－f（a）＝f′（ξ）（b－a）（a＜ξ＜b）

    B

    f（b）－f（x1）＝f′（ξ）（b－x1）（x1＜ξ＜b）

    C

    f（x2）－f（x1）＝f′（ξ）（x2－x1）（x1＜ξ＜x2）

    D

    f（x2）－f（a）＝f′（ξ）（x2－a）（a＜ξ＜x2）


    正确答案： C
    解析：
    考查拉格朗日中值定理的应用。
    值得注意的是，当函数f（x）在[a，b]上连续且在（a，b）内可导时，才可在[a，b]上对函数f（x）应用拉格朗日中值定理。
    由于题中没有说明函数f（x）在[a，b]上连续，因此有可能f（x）在x＝a或x＝b上没有定义，选项中涉及f（a）、f（b）的均为错误选项。

  • 第21题：

    问答题
    设f（x）在（a，b）内二阶可导，且f″（x）≥0，证明：对于（a，b）内任意两点x1、x2及0≤t≤1，有f[（1－t）x1＋tx2]≤（1－t）f（x1）＋tf（x2）。

    正确答案：
    由于不等式中含有f[(1-t)x1+tx2]、f(x1)、f(x2),则应在x0=(1-t)x1+tx2处展开泰勒式,即f(x)=f(x0)+f′(x0)(x-x0)+f″(ξ)(x-x0)2/(2!),ξ介于x和x0之间。
    又f″(x)≥0,则f″(ξ)≥0。故f(x)≥f(x0)+f′(x0)(x-x0)。则
    f(x1)≥f(x0)+f′(x0)(x1-x0)①
    f(x2)≥f(x0)+f′(x0)(x2-x0)②
    ①(1-t)+②t,得(1-t)f(x1)+tf(x2)≥f(x0)+f′(x0)[(1-t)x1+tx2-x0]=f(x0),即(1-t)f(x1)+tf(x2)≥f[(1-t)x1+tx2]。
    解析： 暂无解析

  • 第22题：

    单选题
    设函数f（x）＝x2（x－1）（x－2），则f′（x）的零点个数为（　　）。
    A

    0

    B

    1

    C

    2

    D

    3


    正确答案： A
    解析：
    函数f（x）＝x2（x－1）（x－2），f（0）＝f（1）＝f（2）＝0，由罗尔定理可知，至少有ξ1∈（0，1）、ξ2∈（1，2）使得f′（ξ1）＝0，f′（ξ2）＝0，即f′（x）至少有两个零点。又函数f（x）是四次多项式，故f′（x）是三次多项式，三次方程f′（x）＝0的实根不是一个就是三个，故f′（x）有三个零点。

  • 第23题：

    单选题
    设函数f（u）可导，y＝f（x2），当自变量x在x＝－1处取得增量Δx＝－0.1时，相应的函数的增量Δy的线性主部为0.1，则f′（1）＝（　　）。
    A

    －1

    B

    0.1

    C

    1

    D

    0.5


    正确答案： B
    解析：
    由dy＝f′（x2）dx2＝2xf′（x2）dx，则0.1＝－2f′（1）（－0.1），即f′（1）＝0.5。

相关内容