单选题两曲线y=1/x,y=ax2+b在点(2,1/2)处相切,则( )。A a=-1/16,b=3/4B a=1/16,b=1/4C a=-1,b=9/2D a=1,b=-7/2
题目
a=-1/16,b=3/4
a=1/16,b=1/4
a=-1,b=9/2
a=1,b=-7/2
相似考题
更多“单选题两曲线y=1/x,y=ax2+b在点(2,1/2)处相切,则( )。A a=-1/16,b=3/4B a=1/16,b=1/4C a=-1,b=9/2D a=1,b=-7/2”相关问题
-
第1题:
曲线y=x3—2x在点(1,-1)处的切线方程为 .
正确答案:
y=x-2【考情点拨】本题主要考查的知识点为切线方程.【应试指导】 -
第2题:
11 、点 A ( 2 , y 1 ) 、 B ( 3 , y 2 )是二次函数 y=x 2- 2x+1 的图象上两点,则 y 1 与 y 2 的大小关
系为 y 1 _________ y 2 (填 “ > ” 、 “ < ” 、 “ = ” ) .
正确答案:<
考点:二次函数图象上点的坐标特征。
分析:本题需先根据已知条件求出二次函数的图象的对称轴,再根据点A、B的横坐标的大小即可判断出y1与y2的大小关系.
解答:解:∵二次函数y=x2﹣2x+1的图象的对称轴是x=1,
在对称轴的右面y随x的增大而增大,
∵点A(2,y1)、B(3,y2)是二次函数y=x2﹣2x+1的图象上两点,
23,
∴y1y2.
故答案为:.
点评:本题主要考查了二次函数图象上点的坐标特征,在解题时要能灵活应用二次函数的图象和性质以及点的坐标特征是本题的关键.
-
第3题:
设函数z=x2+3y2-4x+6y-1,则驻点坐标为A.(2,一1)
B.(2,1)
C.(-2,-1)
D.(-2,1)答案:A解析: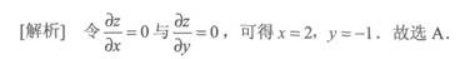
-
第4题:
曲线y=e2x-4x在点(0,1)处的切线方程是()A.2x-y-1=0
B.2x+y-1=0
C.2x-y+1=0
D.2x+y+1=0答案:B解析:【考情点拨】本题考查了曲线的切线方程的知识点.
-
第5题:
曲线y=x3-4x+2在点(1,-1)处的切线方程为( )A.x-y-2-0
B.x-y=0
C.x+y=0
D.x+y-2=0答案:C解析: -
第6题:
曲线y=3x+1在点(1,3)处的切线方程为( )。A、y=2x+1
B、r=4x-1
C、y=4x+2
D、y=3x答案:B解析:先求出y=x3+1在点(1,3)处切线的斜率为4,再根据过(1,3),得到切线方程为y=4x-l。 -
第7题:
若w=1,x=2,y=3,z=4,则表达式w
- A、4
- B、3
- C、2
- D、1
正确答案:D -
第8题:
曲面z=y+lnx/z在点(1,1,1)处的法线方程是:()
- A、(x-1)/1=(y-1)/1=(z-1)/-1
- B、(x-1)/1=(y-1)/1=(z-1)/-2
- C、(x-1)/1=(y-1)/-1=(z-1)/-2
- D、x+y-z=1
正确答案:B -
第9题:
哪一点处,两曲线y=sinx和y=3x的切线平行()。
- A、(1,1)
- B、(-1,1)
- C、(1,-1)
- D、(2,3)
正确答案:A -
第10题:
单选题两曲线y=1/x,y=ax2+b在点(2,1/2)处相切,则( )。Aa=-1/16,b=3/4
Ba=1/16,b=1/4
Ca=-1,b=9/2
Da=1,b=-7/2
正确答案: A解析:
由题意可知,点(2,1/2)即是两曲线相切的切点,又是两曲线的一个交点,且两曲线在该点的切线斜率相等。
由点(2,1/2)在曲线y=ax2+b上,将点带入得4a+b=1/2。
又相切于该点,故切线斜率相等,即导数相等,即-1/x2=2ax,将x=2带入得a=-1/16,故b=3/4。 -
第11题:
判断题信源X的概率分布为P(X)={1/2,1/3,1/6},信源Y的概率分布为P(Y)={1/3,1/2,1/6},则信源X和Y的熵相等。A对
B错
正确答案: 错解析: 暂无解析 -
第12题:
单选题设函数y=f(x)由方程e2x+y-cos(xy)=e-1所确定,则曲线y=f(x)在点(0,1)处的法线方程为( )。Ay+1=x/2
By-1=x/2
Cy+1=x
Dy-1=x
正确答案: B解析:
e2x+y-cos(xy)=e-1方程两边对x求导,得e2x+y(2+y′)+sin(xy)·(y+xy′)=0。当x=0时,y=1,y′=-2,因此,法线方程为y-1=x/2。 -
第13题:
曲线y=x3-5x+l在点(2,-l)处的切线方程为 ( )
A.7x—Y一15—0
B.7x-Y+15=0
C.x+y-1=0
D.z+y+1=0
正确答案:A
本题主要考查的知识点为曲线的切线方程.【应试指导】y=x3-5x+1在点(2,-l)处的切线的斜率为 -
第14题:
设曲线y=^e1?x2与直线x=-1的交点为P,则曲线在点P处的切线方程是( )A.2x-y+2=0
B.2x+y+1=0
C.2x+y-3=0
D.2x-y+3=0答案:D解析:
@## -
第15题:
曲线y=x3+2x在点(1,3)处的法线方程是()A.5x+y-8=0
B.5x-y-2=0
C.x+5y-16=0
D.x-5y+14=0答案:C解析:【考情点拨】本题考查了法线方程的知识点.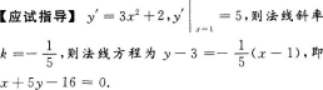
-
第16题:
设函数f(x)具有2阶连续导数,若曲线y=f(x)过点(0,0)且与曲线y=^x在点(1,2)处相切,则 =________.答案:1、2(ln2-1)解析:
=________.答案:1、2(ln2-1)解析:
-
第17题:
曲面z=1-x2-y2在点(1/2,1/2,1/2)处的切平面方程是:A.x+y+z-3/2=0
B.x-y-z+3/2=0
C.x-y+z-3/2=0
D.x-y+z+3/2=0答案:A解析:提示 F(x,y,z)=x2+y2+z-1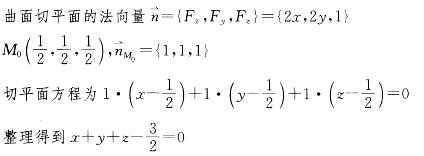
-
第18题:
设曲线y = x3+ax与曲线y= bx2+c在点(-1,0)处相切,则( )。
A. a=b=-1,c=1B. a =-1,b=2,C=-2 C. a=1,b=-2,c=2 D. a=b =-1,c =-1答案:A解析: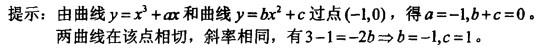
-
第19题:
信源X的概率分布为P(X)={1/2,1/3,1/6},信源Y的概率分布为P(Y)={1/3,1/2,1/6},则信源X和Y的熵相等。
正确答案:正确 -
第20题:
在曲线x=t,y=t2,z=t3上某点的切线平行于平面x+2y+z=4,则该点的坐标为:()
- A、(-1/3,1/9,-1/27),(-1,1,-1)
- B、(-1/3,1/9,-1/27),(1,1,1)
- C、(1/3,1/9,1/27),(1,1,1)
- D、(1/3,1/9,1/27),(-1,1,-1)
正确答案:A -
第21题:
设随机变量X~N(-3,1),Y~N(2,1),且X,Y相互独立,记Z=X-2Y+7,则Z~()。
正确答案:N(0,5) -
第22题:
单选题哪一点处,两曲线y=sinx和y=3x的切线平行()。A(1,1)
B(-1,1)
C(1,-1)
D(2,3)
正确答案: C解析: 暂无解析 -
第23题:
单选题曲线y=x+sin2x在点(π/2,1+π/2)处的切线方程是( )。Ay=x/2+1
By=x+1
Cy=(x+1)/2
Dy=x+1/2
正确答案: C解析:
将y=x+sin2x对x求导得y′=1+2sinxcosx,则点(π/2,1+π/2)处切线斜率y′(π/2)=k|x=π/2=1,则切线方程y-(1+π/2)=x-π/2,即y=x+1。 -
第24题:
单选题设平面α平行于两直线x/2=y/(-2)=z及2x=y=z,且与曲面z=x2+y2+1相切,则α的方程为( )。A4x+2y-z=0
B4x-2y+z+3=0
C16x+8y-16z+11=0
D16x-8y+8z-1=0
正确答案: A解析:
由平面α平行于两已知直线可得,平面α的法向量为:n=(2,-2,1)×(1,2,2)=-3(2,1,-2)。设切点为(x0,y0,z0),则切点处曲面的法向量为(2x0,2y0,-1),故2/(2x0)=1/(2y0)=(-2)/(-1),由此解得x0=1/2,y0=1/4,从而z0=x02+y02+1=21/16,因此α的方程为:2(x-1/2)+(y-1/4)-2(z-21/16)=0,即16x+8y-16z+11=0。
