设Ｘ的取值受限于有限区间［a，b］，则X服从（）分布时，其熵达到最大；如X的均值为，方差受限为，则X服从高斯分布时，其熵达到最大。

题目

设Ｘ的取值受限于有限区间［a，b］，则X服从（）分布时，其熵达到最大；如X的均值为，方差受限为，则X服从高斯分布时，其熵达到最大。

相似考题

1.设X~N(0,1),Y~N(0,1),且X与Y相互独立,则X＋Y服从的分布为()A、X+Y服从N(0，1)B、X+Y不服从正态分布C、X+Y~X2(2)D、X+Y也服从正态分布

2.设X服从λ=2的泊松分布,则x的数学期望和方差分别是多少?

3.设随机变量X服从标准正态分布，则其密度函数φ0(x)=

4.关于中心极限定理，下列说法正确的是( )。A．多个随机变量的平均值(仍然是一个随机变量)服从或近似服从正态分布B．几个相互独立同分布随机变量，其共同分布不为正态分布或未知，但其均值μ和方差σ2都存在，则在n相当大的情况下，样本均值X近似服从正态分布N(μ，σ2/n)C．无论什么分布(离散分布或连续分布，正态分布或非正态分布)，其样本均值X的分布总近似于正态分布D．设n个分布一样的随机变量，假如其共同分布为正态分布N(μ，σ2)，则样本均值X仍为正态分布，其均值不变仍为μ，方差为σ2/n

更多“设Ｘ的取值受限于有限区间［a，b］，则X服从（）分布时，其熵达到最大；如X的均值为，方差受限为，则X服从高斯分布时，其熵达到最大。”相关问题

  • 第1题：

    如果随机变量X服从均值为2，方差为9的正态分布，随机变量Y服从均值为5，方差为16的正态分布，X与Y的相关系数为0.5，那么X+2Y所服从的分布是： （ ）。

    A．均值为12，方差为100的正态分布

    B．均值为12，方差为97的正态分布

    C．均值为10，方差为100的正态分布

    D．不再服从正态分布


    正确答案：B

  • 第2题：

    设总体X服从参数为λ的泊松分布，其中λ未知.X1，…，Xn是取自总体X的样本，则λ的最大似然估计是( ).

    A.
    B.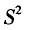
    C.S
    D.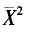

    答案：A
    解析：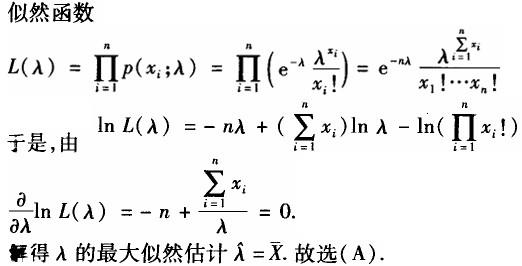

  • 第3题：

    设X,Y都服从标准正态分布,则().


    A.X+Y服从正态分布
    B.X^2+Y服从X2分布
    C.X^2,Y^2都服从χ^2分布
    D.X^2/Y^2服从F分布


    答案：C
    解析：
    因为X，Y不一定相互独立，所以X+Y不一定服从正态分布，同理(B)，(D)也不对，选(C).

  • 第4题：

    设信源X包含4个不同离散消息，当且仅当X中各个消息出现的概率为（）时，信源熵达到最大值，为（），此时各个消息的自信息量为（）。


    正确答案:1/4；2； 2

  • 第5题：

    限平均功率最大熵定理指出对于相关矩阵一定的随机矢量X，当它是正态分布时具有最大熵。


    正确答案:正确

  • 第6题：

    设X服从0—1分布，P=0.6，Y服从λ=2的泊松分布，且X，Y独立，则X+Y（）.

    • A、服从泊松分布
    • B、仍是离散型随机变量
    • C、为二维随机向量
    • D、取值为0的概率为0

    正确答案:B

  • 第7题：

    设X在区间[a，b]上服从均匀分布，则方差DX=a+b


    正确答案:错误

  • 第8题：

    设总体X服从参数为λ的泊松分布，其中λ未知．X1，…，X是取自总体X的样本，则A的最大似然估计是（）．

    • A、X
    • B、S2
    • C、S
    • D、2

    正确答案:A

  • 第9题：

    填空题
    某离散无记忆信源X，其符号个数为n，则当信源符号呈（）分布情况下，信源熵取最大值（）。

    正确答案： 等概,log（n）
    解析： 暂无解析

  • 第10题：

    多选题
    关于中心极限定理的描述正确的是：（）。
    A

    对于n个相互独立同分布的随机变量共同服从正态分布，则样本均值又仍为正态分布

    B

    正态样本均值服从分布N（μ，σ2/n）

    C

    设X1，X2，„，Xn为n个相互独立共同分布随机变量，其共同分布不为正态分布或未知，但其均值和方差都存在，则在n相当大时，样本均值近似服从正态分布

    D

    无论共同分布是什么，只要变量个数n相当大时，均值的分布总近似于正态分布


    正确答案： C,D
    解析： 暂无解析

  • 第11题：

    单选题
    设总体X服从区间[-2，4]上的均匀分布，x1，x2，···，xn为其样本，则( )
    A

    n/3

    B

    1/3

    C

    3/n

    D

    3


    正确答案： C
    解析：

  • 第12题：

    填空题
    设信源X包含4个不同离散消息，当且仅当X中各个消息出现的概率为（）时，信源熵达到最大值，为（），此时各个消息的自信息量为（）。

    正确答案： 1/4,2, 2
    解析： 暂无解析

  • 第13题：

    设随机变量x服从二项分布b(10,O.9),则其均值与标准差分别为( )。A.E(X)=10B.E(X)=9S

    设随机变量x服从二项分布b(10，O．9)，则其均值与标准差分别为（ ）。

    A.E(X)=10

    B.E(X)=9

    C.Vax(X)=0．3

    D.Vax(X)=0．9

    E.Vax(X)=0．3


    正确答案：BD

  • 第14题：

    设服从N(0,1)分布的随机变量X，其分布函数为φ(x)，如果φ(1)=0.84，则P|x|≤1的值是( )。



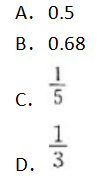    答案：B
    解析：
    X～N(0,1)，P{|x|≤1)=2Φ(1)-1=0.68

  • 第15题：

    设随机变量X和Y都服从正态分布,则().

    A.X+Y一定服从正态分布
    B.(X,Y)一定服从二维正态分布
    C.X与Y不相关,则X,Y相互独立
    D.若X与Y相互独立,则X-Y服从正态分布

    答案：D
    解析：
    若X,Y独立且都服从正态分布，则X,Y的任意线性组合也服从正态分布，选(D).

  • 第16题：

    一维高斯分布的连续信源，其信源熵只与其均值和方差有关。


    正确答案:错误

  • 第17题：

    某离散无记忆信源X，其符号个数为n，则当信源符号呈（）分布情况下，信源熵取最大值（）。


    正确答案:等概；log（n）

  • 第18题：

    设随机变量X服从二项分布B（10，p），若X的方差是5/2，则p=（）


    正确答案:1/2

  • 第19题：

    关于中心极限定理的描述正确的是：（）。

    • A、对于n个相互独立同分布的随机变量共同服从正态分布，则样本均值又仍为正态分布
    • B、正态样本均值服从分布N（μ，σ2/n）
    • C、设X1，X2，„，Xn为n个相互独立共同分布随机变量，其共同分布不为正态分布或未知，但其均值和方差都存在，则在n相当大时，样本均值近似服从正态分布
    • D、无论共同分布是什么，只要变量个数n相当大时，均值的分布总近似于正态分布

    正确答案:A,B,C,D

  • 第20题：

    判断题
    一维高斯分布的连续信源，其信源熵只与其均值和方差有关。
    A

    对

    B

    错


    正确答案： 错
    解析： 暂无解析

  • 第21题：

    单选题
    关于中心极限定理，下列说法正确的是（　　）。
    A

    多个随机变量的平均值（仍然是一个随机变量）服从或近似服从正态分布

    B

    n个相互独立同分布随机变量，其共同分布不为正态分布或未知，但其均值μ和方差σ2都存在，则在n相当大的情况下，样本均值X—近似服从正态分布N（μ，σ2/n）

    C

    无论什么分布（离散分布或连续分布，正态分布或非正态分布），其样本均值X—的分布总近似于正态分布

    D

    设n个分布一样的随机变量，假如其共同分布为正态分布N（μ，σ2），则样本均值X—仍为正态分布，其均值不变仍为μ，方差为σ2/n


    正确答案： C
    解析：
    AC两项成立的前提条件是多个随机变量必须相互独立且同分布；D项要求这些随机变量相互独立。

  • 第22题：

    填空题
    设Ｘ的取值受限于有限区间［a，b］，则X服从（）分布时，其熵达到最大；如X的均值为，方差受限为，则X服从高斯分布时，其熵达到最大。

    正确答案： 均匀;
    解析： 暂无解析

  • 第23题：

    单选题
    设总体X服从参数为λ的泊松分布，其中λ未知．X1，…，X是取自总体X的样本，则A的最大似然估计是（）．
    A

    X

    B

    S2

    C

    S

    D

    2


    正确答案： A
    解析： 暂无解析

相关内容