王某购买了一台固定资产，约定需要从现在开始每年年末偿还1万元，需要偿还n年，利率为i，则这台固定资产的现值是[1-（1+i）-n]/i万元，如果改为每年年初偿还，偿还期数不变，则这台固定资产的现值是（　　）万元。 A.[1-（1+i）-n-1]/i-1 B.[1-（1+i）-n-1]/i+1 C.[1-（1+i）-n+1]/i-1 D.[1-（1+i）-n+1]/i+1

题目
王某购买了一台固定资产，约定需要从现在开始每年年末偿还1万元，需要偿还n年，利率为i，则这台固定资产的现值是[1-（1+i）-n]/i万元，如果改为每年年初偿还，偿还期数不变，则这台固定资产的现值是（　　）万元。

A.[1-（1+i）-n-1]/i-1
B.[1-（1+i）-n-1]/i+1
C.[1-（1+i）-n+1]/i-1
D.[1-（1+i）-n+1]/i+1
相似考题

1.某项目建设期为2年，建设期内每年初贷款1000万元，年利率为8%。若运营期前5年每年末等额偿还贷款本息，到第5年末全部还清。则每年末偿还贷款本息()万元。A.482.36B.520.95C.562.63D.678.23

2.某项目建设期为2年，建设期内每年年初分别贷款600万元和900万元，年利率为10%。若在运营期前5年内于每年年末等额偿还贷款本利，则每年应偿还（ ）万元。A．343.20B．395.70C．411.52D．452.68

3.某工程项目建设期为 2 年，建设期内第 1 年初和第 2 年初分别贷款 600 万元和 400 万元，年利率为 8 ％。若运营期前 3 年每年末等额偿还贷款本息，到第 3 年末全部还清。则每年末应偿还贷款本息（ ）万元。A ． 406.66B ． 439.19C ． 587.69D ． 634.70

4.某企业年初想银行借得一笔款项，有效期利率为10%，偿还期为5年，如果采用等额还本付息方式还款，每年某企业需要偿还164万元。现企业决定采用到期一次还本付息式还款，则到期偿还的本利和是( )万元。A.625B.825C.902D.1001

更多“王某购买了一台固定资产，约定需要从现在开始每年年末偿还1万元，需要偿还n年，利率为i，则这台固定资产的现值是[1-（1+i）-n]/i万元，如果改为每年年初偿还，偿还期数不变，则这台固定资产的现值是（　　）万元。 ”相关问题

  • 第1题：

    某企业为了偿还3年后的债务10万元,从现在开始每年年末进行存款,银行存款利率为10%,则为

    某企业为了偿还３年后的债务10万元，从现在开始每年年末进行存款，银行存款利率为10%，则为了保证还款，每年年末应该存款（ ）元。（ＦＶＡ10%，3＝3.31 ＦＶＡ10%，2＝2.1）

    A．3.02万元

    B．33.1万元

    C．4.76万元

    D．21万元


    正确答案：A
    10/3.31=3.02，用的是偿债基金的公式 

  • 第2题：

    设本金为P，利率为i，本利和为F，计息期数为n，每年末投资为A（在几年内），则现值系数可表示为（　　）。
    A．P（1+i）n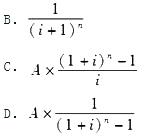


    答案：B
    解析：
    现值是指按规定的贴现率，同某一时间的资金额等值的任何较早时间的资金额。已知终值F，求现值P，可表示为：（P/F，i，n），由公式F=P（1+i）n得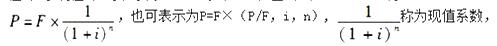：，用PW表示。

  • 第3题：

    假设银行利率为i，从现在开始每年年末存款1元，n年后的本利和为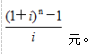

    如果改为每年年初存款，存款期数不变，n年后的本利和应为（）元。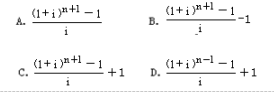


    答案：B
    解析：
    预付年金终值系数与普通年金终值系数相比，期数加1，系数减1。

  • 第4题：

    假设银行利率为i，从现在开始每年年末存款1元，n年后的本利和为（F/A，i，n）元。如果改为每年年初存款，存款期数不变，n年后的本利和应为（　）元。

    A.（F/A，i，n＋1）
    B.（F/A，i，n＋1）－1
    C.（F/A，i，n－1）＋1
    D.（F/A，i，n－1）

    答案：B
    解析：
    预付年金终值系数与普通年金终值系数相比，期数加1，而系数减1。

  • 第5题：

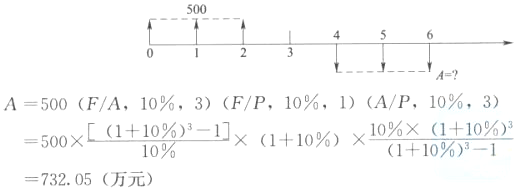
    某工程项目建设期为3年，建设期内每年初贷款500万元，年利率为10%。运营期前3年每年末等额偿还贷款本息，到第3年末全部还清。则每年末应偿还贷款本息（ ）万元。

    A：606.83
    B：665.50
    C：732.05
    D：953.60

    答案：C
    解析：
    2019版教材P162
    关于等值计算考核点，关键是理解等值计算的6个公式和有效利率与名义利率的概念与换算关系，并能灵活运用。历年在该考核点的考核形式万变不离其宗，考生可以针对本考核点多做一些练习题，以加快做题速度。
    这一题其实很简单，因为借款是3年，还款也是3年，所以相当于把0、1、2期的借款，分别搬到了4、5、6期还款，所以就是500*1.1^4=732.05

  • 第6题：

    (2010年)某工程项目建设期为3年，建设期内每年初贷款500万元，年利率为10%，运营期前3年每年末等额偿还贷款本息，到第3年末全部还清，则每年末应偿还贷款本息()万元。

    A.606.83
    B.665.48
    C.732.05
    D.953.66

    答案：C
    解析：
    第三年末应偿还的本息：500×(1+10%)=550万；(500+550)×(1+10%)=1155万；(1155+500)×(1+10%)=1820.5万 运营期三年每年偿还A=P(A/P,i,n)=1820.5×(A/P,10%,3)=1820.5×0.4021=732.05（万元）。

  • 第7题：

    某人第1年年末借款M元，利率为i，按约定从第3年开始到第n年等额还清所有借款，则在第3年到第n年间，每年需偿还()元。

    A:M[i(1+i)n-1]/[(1+i)n-2-1]
    B:M[i(1+i)n-3]/[(1+i)n-2-1]
    C:M[i(1+i)n-2]/[(1+i)n-2-1]
    D:M[i(1+i)n-3]/[(1+i)n-3-1]

    答案：A
    解析：
    画出现金流量图如下图所示：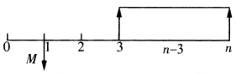

    则第1年的借款在第2年末为M(1+i)元，再利用已知现值求年金的方法，现值为M(1+i)元，年数为(n-2)年，于是年金A=M[i(1+i)n-1]/[(1+i)n-2-1]。

  • 第8题：

    假设银行利率为i，从现在开始每年年末存款1元，n年后的本利和为[（1＋i） n－1]/i元。如果改为每年年初存款，存款期数不变、，n年后的本例和应为（　）元。


    答案：B
    解析：
    预付现金终值系数和普通年金终值系数相比，期数加1，系数减1。

  • 第9题：

    某企业基建3年，每年初向银行贷款100万元，年利率为10%，银行要求企业在第5、第6和第7年的年末等额偿还，则企业每年应偿还（）万元。

    • A、161.04
    • B、177.15
    • C、146.40
    • D、177.69

    正确答案:A

  • 第10题：

    某企业从银行贷款220万元，用于购买某设备，若偿还期为5年，每年末偿还相等的金额，贷款利率为5.55%，每年末应偿还（　）万元。

    • A、38.84(万元)
    • B、46.84(万元)
    • C、51.59(万元)
    • D、68.84(万元)

    正确答案:C

  • 第11题：

    单选题
    某公司年初从银行得到一笔贷款，原约定连续5年每年年末还款10万元，年利率11％，按复利计息。后与银行协商，还款计划改为到第5年年末一次偿还本利，利率不变，则第5年年末应偿还本利和：（）
    A

    54.400万元

    B

    55.500万元

    C

    61.051万元

    D

    62.278万元


    正确答案： C
    解析： 已知A求F，用等额支付系列终值公式计算。

  • 第12题：

    单选题
    某工程项目建设期为3年，建设期内每年初贷款500万元，年利率为10%，运营期前3年每年年末等额偿还贷款本息，到第3年年末全部还清，则每年末应偿还贷款本息（）万元。
    A

    606．83

    B

    665．50

    C

    732．05

    D

    953．60


    正确答案： A
    解析： 将流出的现金流量和流入的现金流量均分别累计折算到运营期第
    1年年初并令其相等，则有：500(f/A，10%，3)(f/P，10%，1)＝A(P/A，10%，3)。
    A＝500(f/A，10%，3)(f/P，10%，1)/(P/A，10%，3)
    ＝500(f/A，10%，3)(f/P，10%，1)×(A/P，10%，3)
    ＝500×[(1＋10%)3－1]/10%×(1＋10%)×10%×(1＋10%)3/[(1＋10%)3－1]
    ＝732．05(万元)
    本题建设期每年年初贷款，注意年金与终值的现金流量模型f在建设期第三年年年初，当研究期限为3年对待用已知A求f的公式时，0时刻在建设期第一年年初再往前虚拟一年的期初。

  • 第13题：

    设本金为P，利率为i，本利和为F，计息期数为n，每年末投资为A(在几年内)，则现值系数可表示为( )。

    A.P(1+i)n
    B.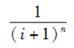
    C.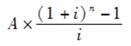
    D.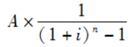

    答案：B
    解析：

  • 第14题：

    企业1~4 年每年年初向银行借款100 万元，借款年利率为10%，预计在6~9 年末等额本息偿还全部借款。则每年年末需要偿还的金额为（ ）万元。

    A.155.28
    B.161.05
    C.177.16
    D.180.36

    答案：C
    解析：
    F=P×（1+10%）^6=100×（1+10%）^6=177.16 万元。

  • 第15题：

    假设银行利率为i，从现在开始每年年末存款1元，n年后的本利和为[（1+i）n-1]/i元。如果改为每年年初存款，存款期数不变，n年后的本利和应为（　　）元。

    A.[（1+i）n+1-1]/i
    B.[（1+i）n+1-1]/i-1
    C.[（1+i）n-1-1]/i+1
    D.[（1+i）n+1-1]/i+1

    答案：B
    解析：
    预付年金终值系数和普通年金终值系数相比，期数加1，系数减1；或者在相同期数的普通年金终值系数基础上，再乘以1+i。

  • 第16题：

    （2014年）假设银行利率为i，从现在开始每年年末存款1元，n年后本利和

    为元。如果改为每年年初存款，存款期数不变，n年后的本利和应为（）元。


    答案：D
    解析：
    预付年金终值系数与普通年金终值系数相比，期数加1，而系数减1。

  • 第17题：

    某项目建设期为2年，建设期内每年初贷款1000万元，年利率为8%。若运营期前5年每年末等额偿还贷款本息，到第5年末全部还清。则每年末偿还贷款本息（ ） 万元。
    A. 482.36 B. 520.95
    C. 562.63 D. 678.23


    答案：C
    解析：
    可画出现金流量表进行分析，把前两年的投资额折算至第二年末求出终值，再由此计算出题目要求的等额年值，计算周期为五年，故
    1000CF/P, 8%, 2)+1000(F/P, 8%, 1)= 2246.4万元
    A=P（A/P, i, n) = 2246.4(A/P，8%, 5) = 562.63
    见教材第二章第一节P39
    【考核要点】等值计算。

  • 第18题：

    企业计划期初向银行借款300万元，期限3年，到期一次偿还本金，按年付息，预计资金筹集费为借款额的5%；所得税税率为25%。若企业希望税后资金成本控制在8%以内，考虑利息的抵税作用后，则该借款的利率不应超过()（注：（P/A,i,n）=[(1+i)n-1]/[i(1+i)n],（A/P,i,n）=[i(1+i)n]/(1+i)n-1]

    A:7.99%
    B:8.08%
    C:8.35%
    D:8.63%

    答案：B
    解析：
    列计算式为：300-300*5%-[300*借款利率*(1-25%)/(1+8%)1]-[300*借款利率*(1-25%)/(1+8%)2]-[300*借款利率*(1-25%)/(1+8%)3]-300/(1+8%)3=0。根据上式可得出，借款利率不应超过8.08%。

  • 第19题：

    企业年初借得50000元贷款，10年期，年利率为12%，每年末等额偿还。已知年金现值系数(P/A，12%，10)=5.6502，则每年应偿还的金额为()元。

    A.8849
    B.5000
    C.6000
    D.28251

    答案：A
    解析：
    根据5000=A×(P/A，12%，10)，得出A=5000/5.6502=8849(元)。

  • 第20题：

    某公司年初从银行得到一笔贷款，原约定连续5年每年年末还款10万元，年利率11％，按复利计息。后与银行协商，还款计划改为到第5年年末一次偿还本利，利率不变，则第5年年末应偿还本利和：（）

    • A、54.400万元
    • B、55.500万元
    • C、61.051万元
    • D、62.278万元

    正确答案:D

  • 第21题：

    某企业第1年年初和第1年年末分别向银行借款300万元，年利率均为10%，复利计息，第3～5年年末等额本息偿还全部借款。则每年年末应偿还金额为（）万元。

    • A、209.43
    • B、230.33
    • C、278.67
    • D、315.68

    正确答案:C

  • 第22题：

    某企业年初向银行借得一笔款项，有效年利率为10%，偿还期为5年，如果采用等额还本付息的方式还款，每年年末企业需要偿还164万元，现企业决定采用到期一次还本付息方式还款，则到期应偿还的本利和是（）万元。

    • A、625
    • B、825
    • C、902
    • D、1001

    正确答案:D

  • 第23题：

    单选题
    某企业从银行贷款1000万元用于项目建设，贷款年利率为8%，计划于每年年末等额偿还，偿还期为8年，则该企业每年末应偿还（　　）万元。
    A

    125.00

    B

    135.50

    C

    174.01

    D

    197.64


    正确答案： C
    解析：
    已知现值为1000万元，利率为8%，期限为8年，年值A＝P（A／P，i，n）＝1000×（A／P，8%，8）＝174.01（万元）。

相关内容