设z=xy，则dz=（）

题目

设z=xy，则dz=（）

相似考题

1.下面规则中，不正确的是（）。A．若X→Y，WY→Z，则XW→ZB．若X→Y，Y→Z，则XY→ZC．若XY→Z，则X→Z，Y→ZD．若X→Y，则Y→Z，刚X→Z

2.(本题满分6分)设函数z=sin(xy)+2x2+y，求dz．

3.下面规则中，不正确的是A．若X→Y，WY→Z，则XW→ZB．若X→Y，Y→Z，则XY→ZC．若XY→Z，则X→Z，Y→ZD．若X→Y，则Y→Z，则X→Z

4.设函数；=arctan(xy)+2x2+y，求dz.

更多“设z=xy，则dz=（） ”相关问题

第1题：

设x，y和z都是int型变量，且x=3，y=4，z=5，则下列表达式中，值为0的表达式是A．x&&y B．x<=y C． x||++y&&y-z D．!（x<y&&!z||1）

正确答案：D
在本题中，定义了三个整型变量x，y，z，并分别赋初值为3，4，5。然后求结果为0的表达式。
选项A中的表达式x&&y，由于在C语言中，有非0即真的定义，即变量x，y的值都不为0，因此表达式的结果不为0。
选项B中的表达式x<=y，由于变量y的值比变量x的值大，因此，该表达式的结果也不为0。
选项C中的表达式x||++y&&y-z，由于运算符&&的优先级较||高，那么本表达式等价于x||（++y&&y-z），在表达式中，首先运算++y，将变量y的值变为5，然后执行y-z，得到结果为0，因此，（++y&&y-z）的运算结果为0，但x为非0值，最终的结果不为0。
选项D中的表达式!（x<y&&!z||1），首先运算!z，结果为0，由此可知x<y&&!z的结果为0，但由于||运算符后有一个1，因此，（x<y&&!z||1）部分的结果为1，而再进行逻辑非运算结果为0。
第2题：

设φ(x,y,z)=xy2z,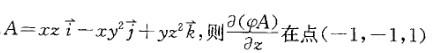处的值为:

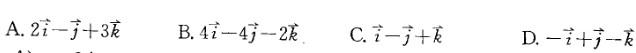答案：A
解析：

(-1)(-1,0,-2)+(-1)(-1,1,-1)=(2,1,-3)
第3题：

设函数z=ln(x+y2)，则全微分dz=_______．

答案：
解析：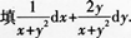
第4题：

设z=sin(xy)+2x2+y，求dz．

答案：
解析：
解法1
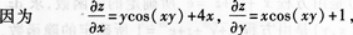
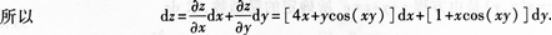
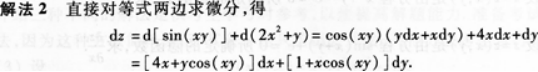
第5题：

设函数z=ex+y，则dz=_______．

答案：
解析：
填exdx+dy．
第6题：

设函数，(u)可导，z=f(sin y-sin x)+xy，则=__________.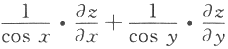

答案：
解析：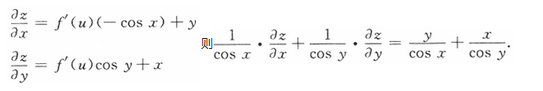
第7题：

设Z=Z(x，Y)是由方程x+y3+z+e2=1确定的函数，求dz

答案：
解析：
利用隐函数求偏导数公式，记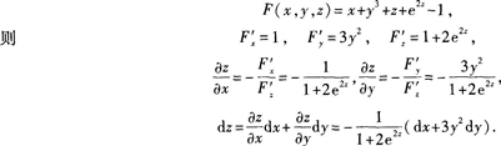
第8题：

设函数z=xy，则全微分dz_______.

答案：
解析：
第9题：

对于关系模式R（X，Y，Z），下列结论错误的是（）
- A、若X→Y，Y→Z，则X→Z
- B、若X→Y，X→Z，则X→YZ
- C、若X→Z，则XY→Z
- D、若XY→Z，则X→Z，Y→Z
正确答案:D
第10题：

填空题
设z＝f（xy，x/y）＋g（y/x），其中f、g均可微，则∂z/∂x＝____。

正确答案： yf₁′+f₂′/y-yg′/x²
解析：
设f₁′为函数f（u，v）对第一中间变量的偏导，f₂′为函数f（u，v）对第二中间变量的偏导，g′为函数g对x的导数。则∂z/∂x＝∂f（xy，x/y）/∂x＋∂g（y/x）/∂x＝f₁′y＋f₂′·（1/y）＋g′·（－y/x²）＝f₁′y＋f₂′/y－yg′/x²。
第11题：

单选题
设f有二阶偏导数，z＝f（xy），则∂2z/∂x∂y等于（　　）。
A
yf″＋f′
B
xy²f″
C
xyf′f″
D
f′＋xyf″

正确答案： B
解析：
∂z/∂x＝yf′，∂²z/∂x∂y＝f′＋yf″·x＝f′＋xyf″。
第12题：

单选题
若z=sin（xy）则它的全微分dz=（）。
A
xcos（xy）
B
（xdx+ydy）cos（xy）
C
ycos（xy）
D
（ydx+xdy）cos（xy）

正确答案： D
解析：暂无解析
第13题：

对于关系模式R(x，Y，Z)，下列结论错误的是(44)。
A．若X→Y，Y→Z，则X→Z
B．若X→Y，X→Z，则X→YZ
C．若X→Z，则XY→Z
D．若XY→Z 则X→Z，Y→Z

正确答案：D
解析：本题考查函数依赖的概念和性质。选项A是传递规则；选项B是合并规则；选项C中，X→Z成立，则给其决定因素　X再加上其他冗余属性Y也成立；选项D不成立，反例：如XY为学号和课程号，Z为成绩，则学号、课程号→成绩成立，但学号→成绩不成立。也可以用证明的方法来判定　D不成立(略)。
第14题：

设函数z=x2ey，则全微分dz=_______．

答案：
解析：
填2xeydx+x2eydy．
第15题：

设z=xy，则dz=()

A.yxy-1dx+xyInxdy
B.xy-1dx+ydy
C.xy(dx+dy)
D.xy(xdx+ydy)

答案：A
解析：
【考情点拨】本题考查了二元函数的全微分的知识点【应试指导】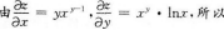
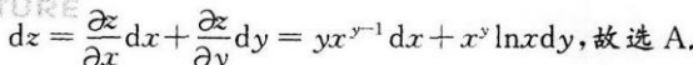
第16题：

设z=z(x，y)是由方程x2+y2+z2=ez所确定的隐函数，求dz．

答案：
解析：
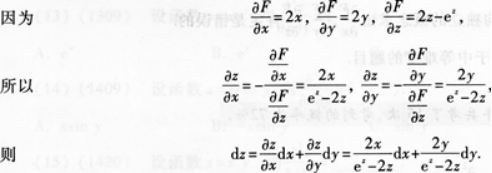
第17题：

设函数f(μ，ν)具有二阶连续偏导数，z=f(x，xy)，则=________.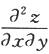

答案：
解析：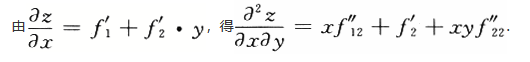
第18题：

设函数z=e2x+y则全微分出dz=______.

答案：
解析：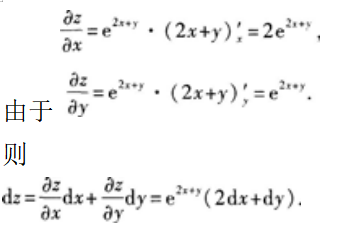
第19题：

设函数z=3x+y2，则dz=__________．

答案：
解析：
3dx+2ydy
第20题：

若z=sin（xy）则它的全微分dz=（）。
- A、xcos（xy）
- B、（xdx+ydy）cos（xy）
- C、ycos（xy）
- D、（ydx+xdy）cos（xy）
正确答案:D
第21题：

填空题
设二元函数z＝xex＋y＋（x＋1）ln（1＋y），则dz|（1，0）＝____。

正确答案： 2edx+(e+2)dy
解析：
由二元函数z＝xe^x^＋^y＋（x＋1）ln（1＋y）得∂z/∂x＝e^x^＋^y＋xe^x^＋^y＋ln（1＋y），∂z/∂y＝xe^x^＋^y＋（x＋1）/（1＋y），故有∂z/∂x|_（₁_，₀_）＝2e，∂z/∂y|_（₁_，₀_）＝e＋2，dz|_（₁_，₀_）＝2edx＋（e＋2）dy。
第22题：

单选题
设z＝z（x，y）是由方程xz－xy＋ln（xyz）＝0所确定的可微函数，则∂z/∂y等于（　　）。[2013年真题]
A
－xz/（xz＋1）
B
－x＋1/2
C
z（－xz＋y）/[x（xz＋1）]
D
z（xy－1）/[y（xz＋1）]

正确答案： B
解析：
将xz－xy＋ln（xyz）＝0两边对y求偏导，得xz_y′－x＋x（z＋y·z_y′）/（xyz）＝0，整理得z_y′＝z（xy－1）/[y（xz＋1）]。
第23题：

单选题
对于关系模式R（X，Y，Z），下列结论错误的是（）
A
若X→Y，Y→Z，则X→Z
B
若X→Y，X→Z，则X→YZ
C
若X→Z，则XY→Z
D
若XY→Z，则X→Z，Y→Z

正确答案： D
解析：本题考查函数依赖的推理规则，显然，只有选项D是错误的

设z=xy，则dz=（）

题目

相似考题

更多“设z=xy，则dz=（） ”相关问题

相关内容