当产品的故障服从指数分布时，故障率为常数λ，此时可靠度的公式是( )。A．B．R(t)=e-λtC．R(t)=eλtD．
题目
当产品的故障服从指数分布时，故障率为常数λ，此时可靠度的公式是( )。
A．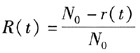
B．R(t)=e-λt
C．R(t)=eλt
D．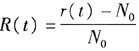
相似考题
参考答案和解析
解析：产品在规定的条件下和规定的时间内，完成规定功能的概率称为可靠度，一般用R(t)表示。当产品的故障服从指数分布时，故障率为常数λ，此时可靠度公式为：R(t)=e-λt。
更多“ 当产品的故障服从指数分布时，故障率为常数λ，此时可靠度的公式是( )。A．B．R(t)=e-λtC．R(t)=eλtD． ”相关问题
-
第1题：
若该产品故障时间服从指数分布，则其故障率入=（ ）。
正确答案：C
-
第2题：
设某一可修复产品的寿命服从指数分布，其故障密度函数f(t)=λe-λt(t≥0)，则下列结论正确的有( )。
A．f(t)=1-e-λt
B．R(t)=e-λt
C．
D．
E．F'(t)=λe-λt
正确答案：BDE
解析：累积故障分布函数F(t)、可靠度函数R(t)和故障密度函数f(t)三者之间的关系为：当产品的故障服从指数分布时，故障率为常数，此时可靠度为：R(t)=e-λt；累积故障分布函数F(t)=1-e-λt，有F'(t)=λe-λt；平均失效(故障)前时间。 -
第3题：
若已知产品的可靠度函数为R(t)=e-λt，则其故障密度函数为( )。
A．1-e-λt
B．-λe-λt
C．λe-λt
D．e-λt
正确答案：C
解析：故障密度函数f(t)是累积故障分布函数F(t)=1-R(t)=1-e-λt的导数，它可以看成在t时刻后的一个单位时间内产品故障的概率，即：=λe-λt。 -
第4题：
设某一可修复产品的寿命服从指数分布，其故障密度函数f(t)=λe-λt(t≥0)，则下列结论正确的有（ ）。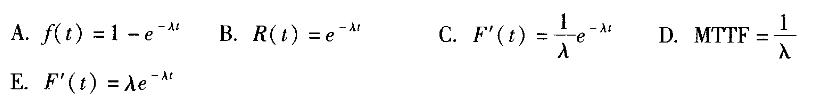
答案：B,D,E解析：
-
第5题：
故障分布服从指数分布的产品，其故障率为λ，当工作时间t=1/λ时，其可靠度等于（）。
A. e-1 B. e-0.1
C.e-0.01
D.e-0.05答案：A解析：当产品的故障服从指数分布时，故障率为常数λ，可靠度公式为：R(t) =e-λt。
故工作时间t=1/λ时，可靠度R(t) =e-λt=e-λx1/λ=e-1。 -
第6题：
设产品的故障率时间服从指数分布，则：
若λ=0.003/h，则t= 100h 的可靠度R(100)为（ ）。
A. e-0.3 B. e-0.035 C. e-0.03 D. e-0.003答案：A解析：当产品的故障服从指数分布时，可靠度函数为R(t) =e-λt ，因此R(100) =e-0.003x100 =e-0.3。 -
第7题：
设产品的故障率时间服从指数分布，则：
若故障率为λ，则有（ ）。
A.可靠度函数R(t) =e-λt B.可靠度函数R(t) =eλt
C.累计故障分布函数F(t) =1-e-λt D.累计故障分布函数F(t) =1-eλt答案：A,C解析：当产品的故障服从指数分布时，故障率为常数，可靠度R(t) =e-λt ，又R(t) + F(t) =1，因此，累计故障分布函数F(t) =1-e-λt 。 -
第8题：
某电子产品的寿命服从指数分布，故障率为0.1/h，则工作4小时不发生故障的概率是（）。
- A、0.33
- B、0.4
- C、0.1
- D、0.67
正确答案:D -
第9题：
假设某产品由20000个电子元器件串联组成，其寿命服从指数分布，如果要求其连续不间断工作3年的可靠度为0.8，元器件的平均故障率为（）。
正确答案:每千万小时1.5 -
第10题：
单选题故障分布服从指数分布的产品，其故障率为λ，当工作时间t=1/λ时，其可靠度等于（ ）。Ae-1
Be-0.1
Ce-0.01
De-0.05
正确答案： B解析：
当产品的故障服从指数分布时，故障率为常数λ，可靠度公式为：R（t）＝e-λt。故工作时间t=1/λ时，可靠度R（t）=e-λt=e-λ×1λ=e-1。 -
第11题：
多选题若故障率为λ，则有（ ）。A可靠度函数R（t）=e-λt
B可靠度函数R（t）=eλt
C累计故障分布函数F（t）=1-e-λt
D累计故障分布函数F（t）=1-eλt
正确答案： A,B解析：
当产品的故障服从指数分布时，故障率为常数，可靠度R（t）=e-λt，又R（t）+F（t）=1，因此，累计故障分布函数F（t）=1-e-λt。 -
第12题：
单选题故障服从指数分布的产品，若工作到MTBF时，其可靠度为（）。A1/e
Be
C0.5
D0.618
正确答案： C解析： 暂无解析 -
第13题：
故障分布服从指数分布的产品，其故障率为λ，当工作时间
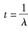时，其可靠度等于( )。A．e-1
B．e-0.1
C．e-0.01
D．e-0.05
正确答案：A
解析：当产品的故障服从指数分布时，故障率为常数λ，可靠度公式为：R(t)=e-λt。故工作时间。 -
第14题：
若该产品故障时间服从指数分布，则其故障率λ=( )。
A．0.0022
B．0.0025
C．0.0029
D．0.0033
正确答案：B
解析：当产品的寿命服从指数分布时，产品的故障率为常数λ，则MTBF=MTTF=1/λ。该产品的故障率。 -
第15题：
故障分布服从指数分布的产品，其故障率为A，当工作时间
时，其可靠度等于（ ）。
正确答案：A
-
第16题：
某产品寿命服从指数分布，即f（t）＝λe﹣u（t≥0）， 则下列说法中，正确的有（）。
A.该产品的可靠度函数为1－e﹣u
B.该产品的不可靠度函数为e﹣u
C.该产品的可靠度函数为e﹣u
D.该产品的故障率为λ
E.该产品的MTBF＝= 1/λ答案：C,D,E解析： -
第17题：
当产品的故障服从指数分布时，故障率为常数λ，此时可靠度的公式是（ ）。
答案：B解析：产品在规定的条件下和规定的时间内，完成规定功能的概率称为可靠度，一般用R(t)表示。当产品的故障服从指数分布时，故障率为常数λ，此时可靠度公式为：R(t)=e-λt。 -
第18题：
设产品的故障率时间服从指数分布，则：
若λ=0.0005/h，则t = 100h的可靠度累计故障概率F(100)为（ ）。
A. 1 -e-0.005 B. 1-e-0.05 C. 1 -e-0.055 D. 1-e-0.5答案：B解析：当产品的故障服从指数分布时，可靠度为：R(t) =e-λt，R(100) =e-0.0005x100 =e-0.05。又产品发生故障和不发生故障是两个对立的事件，则有R(t)+F(t) =1。因此，可靠度累计故障概率F(100) =1 -R(100) =1 -e-0.05。 -
第19题：
故障服从指数分布的产品，若工作到MTBF时，其可靠度为（）。
- A、1/e
- B、e
- C、0.5
- D、0.618
正确答案:A -
第20题：
设产品寿命服从指数分布，在t=MTBF时刻，产品的可靠度为（）。
- A、e1.1
- B、e-0.1
- C、e-l
- D、e-0.001
正确答案:C -
第21题：
单选题若产品的寿命服从指数分布，则故障率的倒数是( )。A平均维修时间
B平均故障间隔时间
C失效概率
D系统可靠性
正确答案： C解析： 暂无解析 -
第22题：
单选题若产品的寿命服从指数分布，则故障率的倒数是（ ）。[2006年真题]A平均维修时间
B平均故障间隔时间
C失效概率
D系统可靠性
正确答案： A解析：
当产品的寿命服从指数分布时，产品的故障率为常数λ，则平均故障间隔时间MTBF＝MTTF＝1/λ。 -
第23题：
填空题假设某产品由20000个电子元器件串联组成，其寿命服从指数分布，如果要求其连续不间断工作3年的可靠度为0.8，元器件的平均故障率为（）。正确答案： 每千万小时1.5解析： 暂无解析