建立3阶幺矩阵A的语句是()。A.A=one(3)B.A=ones(3,1)C.A=one(3,3)D.A=ones(3,3)
题目
建立3阶幺矩阵A的语句是()。
A.A=one(3)
B.A=ones(3,1)
C.A=one(3,3)
D.A=ones(3,3)
相似考题
更多“建立3阶幺矩阵A的语句是()。”相关问题
-
第1题:
设A是一个n阶矩阵,那么是对称矩阵的是( ).
 答案:A解析:
答案:A解析: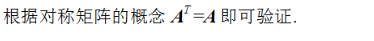
-
第2题:
设A是3阶可逆矩阵,交换A的1,2行得B,则
 答案:D解析:
答案:D解析:
-
第3题:
设为3阶矩阵,将的第2列加到第1列得矩阵,再交换的第2行与第3行得单位矩阵,记,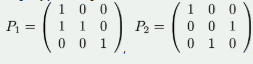 ,则A=( )
,则A=( )
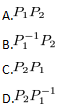 答案:D解析:
答案:D解析:
-
第4题:
设A是3阶矩阵,P=(a1,a2,a3)是3阶可逆矩阵,
若矩阵Q=(a1,a2,a3),则Q-1AQ= 答案:B解析:提示:当P-1AP=Λ时,P=(a1,a2,a3)中a1,a2,a3的排列满足对应关系,a1对应λ1,a2对应λ2,a3对应λ3,可知a1对应特征值λ1=1,a2对应特征值λ2=2,a3对应特征值λ3=0,由此可
答案:B解析:提示:当P-1AP=Λ时,P=(a1,a2,a3)中a1,a2,a3的排列满足对应关系,a1对应λ1,a2对应λ2,a3对应λ3,可知a1对应特征值λ1=1,a2对应特征值λ2=2,a3对应特征值λ3=0,由此可
-
第5题:
设A是4×3阶矩阵且r(A)=2,B= ,则r(AB)=_______.答案:1、2解析:因为|B|=10≠0,所以r(AB)=r(A)=2.
,则r(AB)=_______.答案:1、2解析:因为|B|=10≠0,所以r(AB)=r(A)=2. -
第6题:
设矩阵 是4阶非零矩阵, 且满足
是4阶非零矩阵, 且满足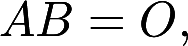 证明矩阵B的秩答案:解析:
证明矩阵B的秩答案:解析:
-
第7题:
设A为n阶非奇异矩阵,α为n维列向量,b为常数.记分块矩阵 .其中A*是矩阵A的伴随矩阵,E是n阶单位矩阵. (1)计算并化简PQ; (2)证明:矩阵Q可逆的充分必要条件是.
.其中A*是矩阵A的伴随矩阵,E是n阶单位矩阵. (1)计算并化简PQ; (2)证明:矩阵Q可逆的充分必要条件是. 答案:解析:
答案:解析: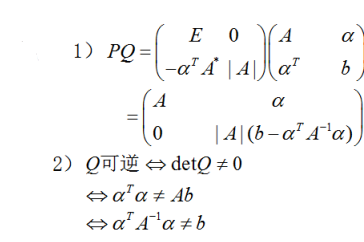
-
第8题:
已知3阶矩阵A的特征值为1,2,-3,求.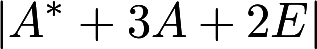 答案:解析:
答案:解析:
-
第9题:
设A是三阶矩阵,有特征值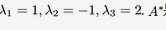 是A的伴随矩阵,E是三阶单位阵,则
是A的伴随矩阵,E是三阶单位阵,则 答案:解析:
答案:解析:
-
第10题:
设A是3阶矩阵,P=(a1,a2,a3)是3阶可逆矩阵,且P-1AP=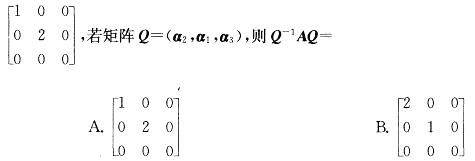
 答案:B解析:提示 当P-1AP=Λ时,P=(a1,a2,a3)中a1,a2,a3的排列满足对应关系,a1对应λ1,a2对应λ2,a3对应λ3,可知a1对应特征值λ1=1,a2对应特征值λ2=2,a3对应特征值
答案:B解析:提示 当P-1AP=Λ时,P=(a1,a2,a3)中a1,a2,a3的排列满足对应关系,a1对应λ1,a2对应λ2,a3对应λ3,可知a1对应特征值λ1=1,a2对应特征值λ2=2,a3对应特征值
-
第11题:
设A是m阶矩阵,B是n阶矩阵,行列式 等于( )。
等于( )。
 答案:D解析:
答案:D解析:
-
第12题:
设3阶矩阵,已知A的伴随矩阵的秩为1,则a=()。
- A、-2
- B、-1
- C、1
- D、2
正确答案:A -
第13题:
与n阶单位矩阵E相似的矩阵是
A.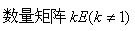
B.对角矩阵D(主对角元素不为1)
C.单位矩阵E
D.任意n阶矩阵A答案:C解析: -
第14题:
已知4阶矩阵A~B,A的特征值为3,4,5,6,E为4阶单位矩阵,则|B-E|=( )A.20
B.60
C.120
D.360答案:C解析:
-
第15题:
设A是3阶实对称矩阵,P是3阶可逆矩阵,B=P-1AP,已知a是A的属于特征值λ的特征向量,则B的属于特征值λ的特征向量是:
A. Pa B. P-1A C. PTa D.(P-1)Ta答案:B解析:
-
第16题:
设A是3阶实对称矩阵,P是3阶可逆矩阵,B=P-1AP,已知α是A的属于特征值λ的特征向量,则B的属于特征值λ的特征向量是:(A) Pα (B) P-1α (C) PTa (D) P(-1)Ta答案:A解析:解:选A。
考察了实对称矩阵的特点,将选项分别代入检验可得到答案。 -
第17题:
A是3阶矩阵,它的特征值互不相等,并且|A|=0,则r(A)=_ .答案:解析:
-
第18题:
设3阶矩阵A 满足 ,证明A可对角化答案:解析:
,证明A可对角化答案:解析:
-
第19题:
设3阶矩阵A,B满足AB=A+B.证明A-E可逆.答案:解析:
-
第20题:
设A为m阶正定矩阵,B为m×n阶实矩阵.证明:B^SAB正定的充分必要条件是r(B)=n,答案:解析:
-
第21题:
设A为3阶实对称矩阵,A的秩为2,且.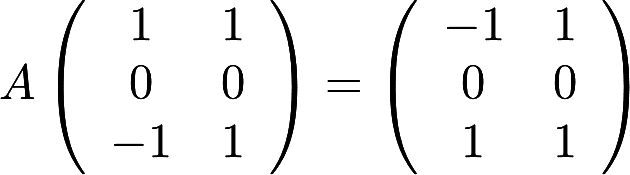 (Ⅰ)求A的特征值与特征向量; (Ⅱ)求矩阵A答案:解析:
(Ⅰ)求A的特征值与特征向量; (Ⅱ)求矩阵A答案:解析:
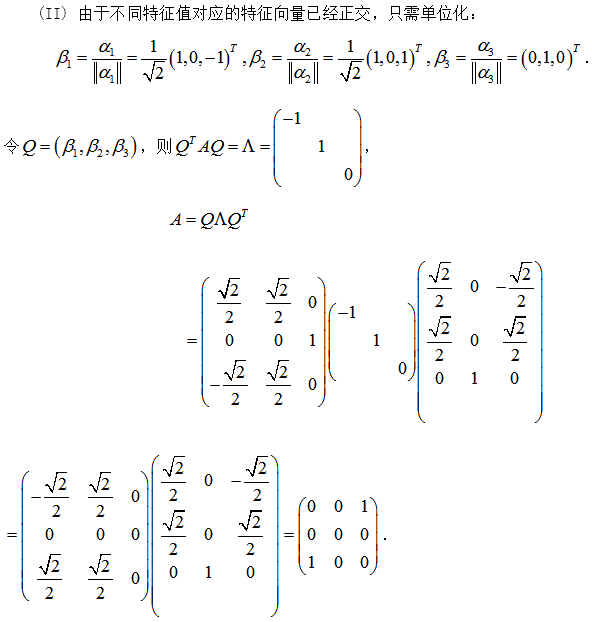
-
第22题:
设A为3阶矩阵.P为3阶可逆矩阵,且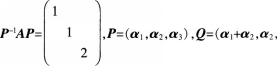
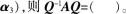
A.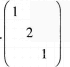
B.
C.
D.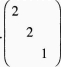 答案:B解析:
答案:B解析: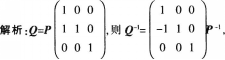
 故选B。
故选B。 -
第23题:
设A是3阶矩阵,P = (α1,α2,α3)是3阶可逆矩阵,且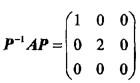 ,若矩阵Q=(α2,α1,α3),则Q-1AQ=( )。
,若矩阵Q=(α2,α1,α3),则Q-1AQ=( )。
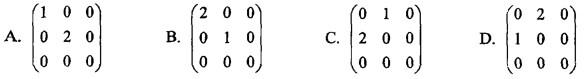 答案:B解析:提示:由条件知,λ1=1,λ2=2,λ3=0是矩阵A的特征值,而α1,α2,α3是对应的特征向量,故有
答案:B解析:提示:由条件知,λ1=1,λ2=2,λ3=0是矩阵A的特征值,而α1,α2,α3是对应的特征向量,故有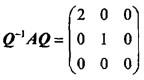 。
。 -
第24题:
单选题(2009)设A是3阶实对称矩阵,P是3阶可逆矩阵,B=P-1AP,已知α是A的属于特征值λ的特征向量,则B的属于特征值λ的特征向量是:()APα
BP-1α
CPTα
D(P-1)Tα
正确答案: C解析: 暂无解析
