若将一个圆柱体木块过轴切成四块，表面积增加168平方厘米，若与上下底面平行将它切成三块，表面积增加113．04平方厘米。求将它削成最大的圆锥体，体积减少多少立方厘米?(π的值为3．14)

题目
若将一个圆柱体木块过轴切成四块，表面积增加168平方厘米，若与上下底面平行将它切成三块，表面积增加113．04平方厘米。求将它削成最大的圆锥体，体积减少多少立方厘米?(π的值为3．14)

相似考题

1.把一个棱长6cm的正方体切成棱长2cm的小正方体。可以得到多少个小正方体？表面积增加了多少？

2.一个体积为3立方分米的长方体，现将它等分成体积为3立方厘米的长方体，则可分成多少个?（ ）A．10B．100C．1 000D．10 000

3.把一个圆柱体削成一个最大的圆锥体，这个圆锥体与原来圆柱体削去部分的体积比是（ ）。A．1：2B．1：3C．2：3D．2：1

4.由棱长是5cm的正方体搭成左边的图形，共有多少个正方体？它的体积是多少立方厘米？它的表面积是多少平方厘米？

更多“若将一个圆柱体木块过轴切成四块，表面积增加168平方厘米，若与上下底面平行将它切成三块，表面积增加113．04平方厘米。求将它削成最大的圆锥体，体积减少多少立方厘米?(π的值为3．14) ”相关问题

  • 第1题：

    今有底面半径和高均为1的圆柱体与底面半径和高均为2的圆柱体，共计15个，表面积和为120π。那么底面半径和高均为2的圆柱体有多少个?

    A．4

    B．5

    C．6

    D．7


    正确答案：B
    [答案] B。[解析]底面半径和高均为1的圆柱体的表面积为2×π×12+2×π×1×1=4π，半径和高均为2的圆柱体的表面积为2×π×22×π×2×2=16π。则半径和高均为2的圆柱体有(120π-15×4π)+(16π-4π)=5个。

  • 第2题：

    从底面半径为1，高为4的圆柱体中掏出一个长方体，然后再在这个长方体中掏出一个最大的圆柱体，则掏出的圆柱体体积最大为（)。


    答案：C
    解析：
    要想掏出的圆柱体的体积最大，则要求在此之前掏出的长方体的底面为正方形,其横截面如图所示：

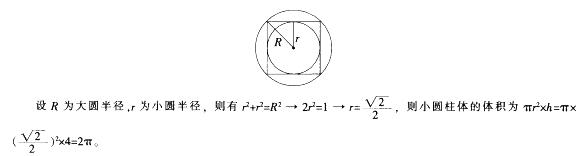
  • 第3题：

    将一个表面积为18平方厘米的正方体沿对角线切成两块对称的三棱柱（见右图），并将这两块三棱柱重新拼接成一个大的三棱柱。则这个大三棱柱的表面积最大为多少平方厘米：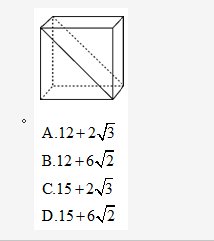

    。
    AA
    BB
    CC
    DD


    答案：D
    解析：

  • 第4题：

    一个长方体木块恰能切割成五个正方体木块，五个正方体木块表面积之和比原来的长方体木块的表面积增加了200cm2。则长方体木块的体积为多少?

    A.625cm3
    B.125cm3
    C.500cm3
    D.750cm3

    答案：A
    解析：
    第一步，本题考查几何问题，属于立体几何类。
    第二步，如图所示，长方体分为5个小正方体，增加了4×2=8（个）阴影部分小正方形的面积，则每个小正方形面积为200÷8=25（cm2），边长为5cm。那么大长方体的体积为5×25×5=625（cm3）。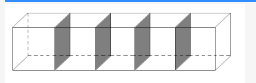

    因此，选择A选项。

  • 第5题：

    圆锥体体积是相同高度和底面直径圆柱体体积的（）。

    • A、1/2；
    • B、1/3；
    • C、1/4；
    • D、1/5。

    正确答案:B

  • 第6题：

    一个大木块重8N，在下列哪种情况下，它的重力不是8N（）

    • A、将它竖直抛出
    • B、将它放到月球上
    • C、将它放在加速上升的电梯内
    • D、将它放到水里，它浮在水面上

    正确答案:B

  • 第7题：

    一个圆锥体的底面周长是一个圆柱体底面周长的2倍，这个圆柱的高是这个圆锥高的2倍，这个圆锥体和圆柱体体积的最简单的整数比是（）

    • A、1：2
    • B、3：1
    • C、3：2
    • D、2：3

    正确答案:D

  • 第8题：

    计算题：有一圆锥体，底面直径D=20cm，高h=50cm，求它的体积。（π=3.14）


    正确答案:圆锥体的体积V=π（D/2）2h/3=3.14×（20/2）2×50/3=5233.3cm3。

  • 第9题：

    单选题
    一个棱长为8㎝2的立方体，表面涂满油漆，现在将它切成棱长为0.5㎝的小立方体，问两个表面有油漆的小立方体有多少个？（　　）
    A

    144

    B

    168

    C

    192

    D

    256


    正确答案： C
    解析：
    两个表面有油漆的小立方体均分布在大立方体的12条棱的周围，每条棱可分8÷0.5＝16段，即共有16个小立方体，又由于16个小立方体中，在每条棱的两端的两个小立方体三面有油漆，因此每条棱上只有14个小立方体两个表面有油漆，则两个表面有油漆的小立方体共有12×14＝168个。

  • 第10题：

    单选题
    一个圆柱体和一个圆锥体的底面积相等，圆锥的高是圆柱高的3倍。则圆锥的体积（）圆柱的体积。
    A

    小于

    B

    等于

    C

    大于


    正确答案： B
    解析： 暂无解析

  • 第11题：

    单选题
    把一个圆柱体削成一个最大的圆锥体，这个圆锥体与原来圆柱体削去部分的体积比是（）
    A

    1：2

    B

    1：3

    C

    2：3

    D

    2：1


    正确答案： B
    解析： 暂无解析

  • 第12题：

    一个圆锥的轴截面平行于投影面，圆锥的正投影是边长为3的等边三角形，求圆锥的体积和表面积。

  • 第13题：

    如图所示，长方形卡纸的长为33．12cm，利用图中的阴影部分正好能做成一个圆柱体(接头忽略不计，π取3．14)。则这个圆柱体的表面积为______。


    答案：
    解析：
    502．4cm2。解析：设该圆柱体的半径为r，则2r+2πr=33．12，解得r=4，圆柱的高h=4r=16，故该圆柱均表面积S=2πr2+2πrh=502．4cm2。

  • 第14题：

    一实心圆锥体的底面半径为r，母线长为2r。若截圆锥体得到两个同样的椎体（如下图所示），则所得两个椎体的表面积之和与原圆椎体表面积的比值是（ ）


    A． B． C． D．

    答案：C
    解析：
    由圆锥体的底面半径为r，母线长为2r，可得圆锥体的表面积为。
    所截得的两个锥体的表面积之和要比原圆锥体的表面积多两个等边三角形截面的面积，等边三角形的边长为2r，则其面积为，所以两个锥体的表面积之和为。则两个锥体的表面积之和与原锥体表面积比值是。C项当选。

  • 第15题：

    已知圆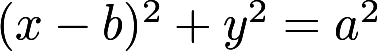, 其中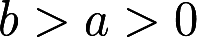, 求此圆绕y轴旋转所构成的旋转体体积和表面积.


    答案：
    解析：

  • 第16题：

    灯泡A的标称值为"220v100w"，灯泡B的标称值为"220v25w"，若将它们串联在220v电压上，求灯A和灯B实际消耗的功率分别是多少？


    正确答案: P=UI 串联线路电流I相等 即：U=P
    U2=25/I U1=100/I
    U1＋U2=U
    U1=176V U2=44V
    推出：Pa＝U1/220×100=80（W）
    Pb＝U2／220×100＝20（W）

  • 第17题：

    把一个圆柱体削成一个最大的圆锥体，这个圆锥体与原来圆柱体削去部分的体积比是（）

    • A、1：2
    • B、1：3
    • C、2：3
    • D、2：1

    正确答案:A

  • 第18题：

    一个圆柱体和一个圆锥体的底面积相等，圆锥的高是圆柱高的3倍。则圆锥的体积（）圆柱的体积。

    • A、小于
    • B、等于
    • C、大于

    正确答案:B

  • 第19题：

    单选题
    一个棱长为8㎝的立方体，表面涂满油漆，现在将它切成棱长为0.5㎝的小立方体，问两个表面有油漆的小立方体有多少个？（　　）
    A

    144

    B

    168

    C

    192

    D

    256


    正确答案： A
    解析：
    两个表面有油漆的小立方体均分布在大立方体的12条棱的周围，每条棱可分8÷0.5＝16段，即共有16个小立方体。又由于16个小立方体中，在每条棱的两端的两个小立方体三面有油漆，因此每条棱上只有14个小立方体两个表面有油漆，则两个表面有油漆的小立方体共有12×14＝168个。

  • 第20题：

    单选题
    一个棱长为8cm的立方体，表面涂满油漆，现在将它切成棱长为0.5cm的小立方体，问两个表面有油漆的小立方体有多少个？（　　）
    A

    144

    B

    168

    C

    192

    D

    256


    正确答案： D
    解析：
    两个表面有油漆的小立方体均分布在大立方体的12条棱的周围，每条棱可分8÷0.5＝16段，即共有16个小立方体。又由于16个小立方体中，在每条棱的两端的两个小立方体三面有油漆，因此每条棱上只有14个小立方体两个表面有油漆，则两个表面有油漆的小立方体共有12×14＝168个。

  • 第21题：

    单选题
    一个圆锥体的底面周长是一个圆柱体底面周长的2倍，这个圆柱的高是这个圆锥高的2倍，这个圆锥体和圆柱体体积的最简单的整数比是（）
    A

    1：2

    B

    3：1

    C

    3：2

    D

    2：3


    正确答案： C
    解析： 暂无解析

相关内容