若n阶方阵A与B相似，则A与B一定等价。
题目
若n阶方阵A与B相似，则A与B一定等价。
相似考题
更多“若n阶方阵A与B相似，则A与B一定等价。”相关问题
-
第1题：
设AB为门阶方阵，若AB等价，则AB相似答案：错解析： -
第2题：
设A为三阶可逆方阵，则( )与A等价。A.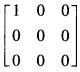
B.
C.
D.
答案：B解析：利用可逆阵与单位阵等价。 -
第3题：
设A，B为n阶矩阵，考虑以下命题：①若A，B为等价矩阵，则A，B的行向量组等价②若行列式.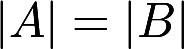
，则A，B为等价矩阵③若
与
都只有零解，则A，B为等价矩阵④若A，B为相似矩阵，则
与
的解空间的维数相同以上命题中正确的是（ ）.
A.①③
B.②④
C.②③
D.③④答案：D解析：
-
第4题：
若n阶矩阵A，B有共同的特征值，且各有n个线性无关的特征向量，则（ ）
A.A与B相似
B.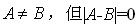
C.A=B
D.A与B不一定相似，但|A|=|B|答案：A解析： -
第5题：
设A与B都是n阶方阵,且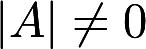
,证明AB与BA相似.答案：解析：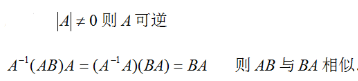
-
第6题：
设 A为 n 阶方阵，B是 A 经过若干次初等行变换得到的矩阵，则下列结论正确的是（ ）。A.|A|=|B|
B.|A|≠|B|
C.若|A|=0，则一定有 |B|=0
D.若 |A|＞ 0，则一定有 |B|＞ 0答案：C解析：本题主要考查矩阵的初等变换及行列式的主要性质。对矩阵可以做如下三种变换：（1）对调两行，记作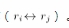
（2）以数 乘某一行的所有元素，记作 。（3）把某一行所有元素的 k 倍加到另一行对应的元素上去，记作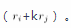
若方阵 A 经过以上三种初等变换得到方阵 B，则对应的行列式的关系依次为 |A|=–|B|，k|A|=|B|，|A|=|B|，即 |A|=a|B|， a∈R （a ≠ 0）。所以 |A|=0 时，必有 |B|=0。C项正确。
A、B、D三项：均为干扰项。与题干不符，排除 -
第7题：
设A，B都是n阶矩阵，若有可逆矩阵P使得P-1AP=B，则称矩阵A与矩阵B（）。
- A、等价
- B、相似
- C、合同
- D、正交
正确答案:B -
第8题：
填空题设A、B、C均为n阶方阵，若A＝CTBC，且|B|＜0，则|A|____。正确答案： ≤0解析：
由行列式性质可知|A|＝|CT|·|B|·|C|＝|C|2·|B|≤0。 -
第9题：
单选题设A为n阶方阵，若对任意n×m（m≥n）矩阵B都有AB＝0，则A＝（ ）。A0
B1
C2
D3
正确答案： A解析：
取基本单位向量组为ε1，ε2，…，εn。
当m＝n时，由对任意B都有AB＝0，则对B＝（ε1，ε2，…，εn）＝En也成立，即AE＝0，故A＝0。
当m＞n时，取B＝（ε1，ε2，…，εn，B1）＝（En，B1），则由AB＝A（En，B1）＝0，知AEn＝0，故A＝0。 -
第10题：
单选题设A、B、C均为n阶方阵，若A＝CTBC，且|B|＜0，则|A|（ ）。A＝0
B＞0
C≤0
D＜0
正确答案： B解析：
由行列式性质可知|A|＝|CT|·|B|·|C|＝|C|2·|B|≤0。 -
第11题：
设A，B是n（n≥2）阶方阵，则必有（ ）.
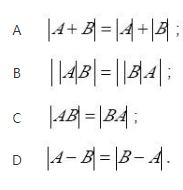答案：C解析： -
第12题：
设n阶矩阵A与对角矩阵相似,则().A.A的n个特征值都是单值
B.A是可逆矩阵
C.A存在n个线性无关的特征向量
D.A一定为n阶实对称矩阵答案：C解析：矩阵A与对角阵相似的充分必要条件是其有n个线性无关的特征向量，A有n个单特征值只是其可对角化的充分而非必要条件，同样A是实对称阵也是其可对角化的充分而非必要条件，A可逆既非其可对角化的充分条件，也非其可对角化的必要条件，选(C). -
第13题：
设A、B均为n阶方阵，则下列式子中错误的是（ ）.
答案：D解析：
-
第14题：
设n阶矩阵A与B等价, 则必须
答案：D解析：
-
第15题：
若n阶方阵A满足|A|＝b（b≠0，n≥2），而A*是A的伴随矩阵，则行列式|A*|等于（ ）。A．bn
B．bn－1
C．bn－2
D．bn－3答案：B解析：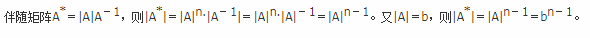
-
第16题：
设A为n阶方阵，A*是A的伴随矩阵，则||A|A*|等于（ ）.
答案：D解析：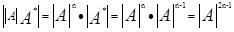
-
第17题：
问答题试证若n阶矩阵A满足A2－A＝2E，则A一定相似于对角矩阵。正确答案：
设λ是矩阵A的特征值,则矩阵f(A)=A2-A-2E的特征多项式为f(λ)=λ2-λ-2,所以有矩阵A的特征值只可能是2或-1。
①当λ=-1是A的特征值,而λ=2不是A的特征值,则有,A-2E,≠0,即(A-2E)可逆。由A2-A-2E=0得(A-2E)(A+E)=0,所以有(A-2E)-1(A-2E)(A+E)=(A-2E)-1·0,即A+E=0,A=-E。因此A相似与对角矩阵-E。
②当λ=2是A的特征值,而λ=-1不是A的特征值,同理于①,可得矩阵A相似与对角矩阵2E。
③当λ=2和λ=-1都是A的特征值,由(A-2E)(A+E)=0知r(A-2E)+r(A+E)≤n。又r(A-2E)+r(A+E)=r(2E-A)+r(A+E)≥r(2E-A+A+E)=r(3E)=n,所以r(A-2E)+r(A+E)=n,即[n-r(A-2E)]+[n-r(A+E)]=n。故两方程组(A-2E)X=0和(A+E)X=0的基础解系所含解向量的个数之和为n,所以A有n个线性无关的特征向量,故其可相似于对角矩阵。解析： 暂无解析 -
第18题：
单选题设A，B都是n阶矩阵，若有可逆矩阵P使得P-1AP=B，则称矩阵A与矩阵B（）。A等价
B相似
C合同
D正交
正确答案： B解析： 由相似矩阵的定义知B正确。故选B。 -
第19题：
填空题设A为n阶方阵，若对任意n×m（m≥n）矩阵B都有AB=0，则A=____.正确答案： 0解析：
取基本单位向量组为ε1，ε2，…εn
当m=n时，由对任意B都有AB=0，则对B=（ε1，ε2，…εn）=En也成立，即AE=0，故A=0．
当m>n时，取B=（ε1，ε2，…εn，B1）=（En，B1），则由AB=A（En，B1）=0，知AEn=0，故A=0． -
第20题：
单选题设A为n阶方阵，B是A经过若干次矩阵的初等变换后所得到的矩阵，则有（ ）。A｜A｜＝｜B｜
B｜A｜≠｜B｜
C若｜A｜＝0，则一定有｜B｜＝0
D若｜A｜＞0，则一定有｜B｜＞0
正确答案： A解析：
矩阵A经过若干次初等变换后得到矩阵B，则存在可逆矩阵P，Q使得B＝PAQ，因此|B|＝|PAQ|＝|P|·|A|·|Q|，若|A|＝0，则必有|B|＝|P|·|A|·|Q|＝0成立。