若n阶矩阵A,B有共同的特征值,且各有n个线性无关的特征向量,则()A、A与B相似B、A≠B，但|A-B|=0C、A=BD、A与B不一定相似，但|A|=|B|

题目
若n阶矩阵A,B有共同的特征值,且各有n个线性无关的特征向量,则()

A、A与B相似

B、A≠B，但|A-B|=0

C、A=B

D、A与B不一定相似，但|A|=|B|

相似考题

1.可对角化的矩阵是____。A.实对称阵B.有n个相异特征值的n阶阵C.有n个线性无关的特征向量的n阶方阵

2.设A是n阶矩阵，且Ak=O(k为正整数)，则( )。A.A一定是零矩阵 B.A有不为0的特征值 C.A的特征值全为0 D.A有n个线性无关的特征向量

3.若n阶矩阵A，B有共同的特征值，且各有n个线性无关的特征向量，则（ ）A.A与B相似 B. C.A=B D.A与B不一定相似，但|A|=|B|

4.设n阶矩阵A与对角矩阵相似,则().A.A的n个特征值都是单值 B.A是可逆矩阵 C.A存在n个线性无关的特征向量 D.A一定为n阶实对称矩阵

参考答案和解析
参考答案：A
更多“若n阶矩阵A,B有共同的特征值,且各有n个线性无关的特征向量,则() ”相关问题

  • 第1题：

    若n阶矩阵A，B有共同的特征值，且各有n个线性无关的特征向量，则（ ）《》（ ）

    A.A与B相似
    B.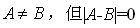
    C.A=B
    D.A与B不一定相似，但|A|=|B|


    答案：A
    解析：

  • 第2题：

    若n阶方阵A与某个对角矩阵相似，则（）

    A．R(A)=n

    B．A有n个不同的特征值

    C．A有n个线性无关的特征向量

    D．A必为对称矩阵


    A有n个线性无关的特征向量

  • 第3题：

    设矩阵A为n阶实矩阵，n为奇数，则下列叙述正确的是________

    A．矩阵A一定有实特征值

    B．矩阵A可能有复特征值

    C．矩阵A有n个线性无关的特征向量

    D．矩阵A线性无关的特征向量个数可能少于n


    设Ap (i) =λ i p (i) i=12…n．已知当i≠j时p (i)T p (j) =0．因此 p (i)T Ap (j) =λ j p (i)T p (j) =0 i≠j．故p (1) p (2) …p (n) 关于A共轭． 设Ap(i)=λip(i),i=1,2,…,n．已知当i≠j时,p(i)Tp(j)=0．因此p(i)TAp(j)=λjp(i)Tp(j)=0,i≠j．故p(1),p(2),…,p(n)关于A共轭．

  • 第4题：

    1、下列说法错误的是（）。

    A．n阶矩阵A可对角化的充要条件是A有n个互异的特征值

    B．n阶矩阵A可对角化的充要条件是A^T有n个互异的特征值

    C．n阶矩阵A可对角化的充要条件是A有n个互异的特征向量

    D．n阶矩阵A可对角化的充要条件是A有n个线性无关的特征向量


    单矩阵 A不是正交矩阵。

  • 第5题：

    下列说法错误的是（）。

    A．n阶矩阵A可对角化的充要条件是A有n个互异的特征值

    B．n阶矩阵A可对角化的充要条件是A^T有n个互异的特征值

    C．n阶矩阵A可对角化的充要条件是A有n个互异的特征向量

    D．n阶矩阵A可对角化的充要条件是A有n个线性无关的特征向量


    A 的列向量组线性相关

相关内容