若n阶方阵A与某个对角矩阵相似，则（）A．R(A)=nB．A有n个不同的特征值C．A有n个线性无关的特征向量D．A必为对称矩阵

题目

若n阶方阵A与某个对角矩阵相似，则（）

A．R(A)=n

B．A有n个不同的特征值

C．A有n个线性无关的特征向量

D．A必为对称矩阵

相似考题

1.可对角化的矩阵是____。A.实对称阵B.有n个相异特征值的n阶阵C.有n个线性无关的特征向量的n阶方阵

2.若n阶矩阵A,B有共同的特征值,且各有n个线性无关的特征向量,则()A、A与B相似B、A≠B，但|A-B|=0C、A=BD、A与B不一定相似，但|A|=|B|

3.节点导纳矩阵的特点有()。A、是n×n阶方阵B、是稀疏矩阵C、一般是对称矩阵D、其对角元一般小于非对角元

4.若A是____,则A必为方阵。A.对称矩阵B.可逆矩阵C.n阶矩阵的转置矩阵D.线性方程组的系数矩阵

参考答案和解析
A有n个线性无关的特征向量
更多“若n阶方阵A与某个对角矩阵相似，则（）”相关问题

  • 第1题：

    若方阵A与B相似，则有（ ）.

    A.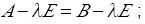
    B.|A|=|B|：
    C.对于相同的特征值λ，矩阵A与B有相同的特征向量：
    D.A与B均与同一个对角矩阵相似.


    答案：B
    解析：

  • 第2题：

    与n阶单位矩阵E相似的矩阵是

    A.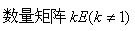
    B.对角矩阵D（主对角元素不为1）
    C.单位矩阵E
    D.任意n阶矩阵A


    答案：C
    解析：

  • 第3题：

    设N阶矩阵A与对角矩阵合同,则A是().

    A.可逆矩阵
    B.实对称矩阵
    C.正定矩阵
    D.正交矩阵

    答案：B
    解析：

  • 第4题：

    下列结论中正确的是（　　）。

    A、 矩阵A的行秩与列秩可以不等
    B、 秩为r的矩阵中，所有r阶子式均不为零
    C、 若n阶方阵A的秩小于n，则该矩阵A的行列式必等于零
    D、 秩为r的矩阵中，不存在等于零的r-1阶子式

    答案：C
    解析：
    A项，矩阵A的行秩与列秩一定相等。B项，由矩阵秩的定义可知，若矩阵A（m×n）中至少有一个r阶子式不等于零，且r＜min（m，n）时，A中所有的r+1阶子式全为零，则A的秩为r。即秩为r的矩阵中，至少有一个r阶子式不等于零，不必满足所有r阶子式均不为零。C项，矩阵A的行列式不等于零意味着矩阵A不满秩，n阶矩阵的秩为n时，所对应的行列式的值大于零；当n阶矩阵的秩＜n时，所对应的行列式的值等于零。D项，秩为r的矩阵中，有可能存在等于零的r-1阶子式，如秩为2的矩阵



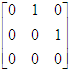
    中存在等于0的1阶子式。

  • 第5题：

    证明n阶矩阵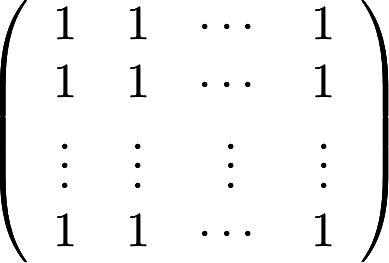与相似


    答案：
    解析：

  • 第6题：

    若n阶方阵A满足|A|＝b（b≠0，n≥2），而A*是A的伴随矩阵，则行列式|A*|等于（　　）。

    A．bn
    B．bn－1
    C．bn－2
    D．bn－3

    答案：B
    解析：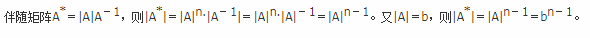

  • 第7题：

    设A，B都是n阶矩阵，若有可逆矩阵P使得P-1AP=B，则称矩阵A与矩阵B（）。

    • A、等价
    • B、相似
    • C、合同
    • D、正交

    正确答案:B

  • 第8题：

    问答题
    试证若n阶矩阵A满足A2－A＝2E，则A一定相似于对角矩阵。

    正确答案：
    设λ是矩阵A的特征值,则矩阵f(A)=A2-A-2E的特征多项式为f(λ)=λ2-λ-2,所以有矩阵A的特征值只可能是2或-1。
    ①当λ=-1是A的特征值,而λ=2不是A的特征值,则有,A-2E,≠0,即(A-2E)可逆。由A2-A-2E=0得(A-2E)(A+E)=0,所以有(A-2E)-1(A-2E)(A+E)=(A-2E)-1·0,即A+E=0,A=-E。因此A相似与对角矩阵-E。
    ②当λ=2是A的特征值,而λ=-1不是A的特征值,同理于①,可得矩阵A相似与对角矩阵2E。
    ③当λ=2和λ=-1都是A的特征值,由(A-2E)(A+E)=0知r(A-2E)+r(A+E)≤n。又r(A-2E)+r(A+E)=r(2E-A)+r(A+E)≥r(2E-A+A+E)=r(3E)=n,所以r(A-2E)+r(A+E)=n,即[n-r(A-2E)]+[n-r(A+E)]=n。故两方程组(A-2E)X(→)=0(→)和(A+E)X(→)=0(→)的基础解系所含解向量的个数之和为n,所以A有n个线性无关的特征向量,故其可相似于对角矩阵。
    解析： 暂无解析

  • 第9题：

    单选题
    若n阶方阵A满足|A|＝b（b≠0，n≥2），而A*是A的伴随矩阵，则行列式|A*|等于（　　）。[2019年真题]
    A

    bn

    B

    bn－1

    C

    bn－2

    D

    bn－3


    正确答案： B
    解析：
    伴随矩阵A*＝|A|A－1，则|A*|＝|A|n·|A－1|＝|A|n·|A|－1＝|A|n－1。又|A|＝b，则|A*|＝|A|n－1＝bn－1。

  • 第10题：

    单选题
    设A为n阶方阵，若对任意n×m（m≥n）矩阵B都有AB＝0，则A＝（　　）。
    A

    0

    B

    1

    C

    2

    D

    3


    正确答案： A
    解析：
    取基本单位向量组为ε(→)1，ε(→)2，…，ε(→)n。
    当m＝n时，由对任意B都有AB＝0，则对B＝（ε(→)1，ε(→)2，…，ε(→)n）＝En也成立，即AE＝0，故A＝0。
    当m＞n时，取B＝（ε(→)1，ε(→)2，…，ε(→)n，B(→)1）＝（En，B(→)1），则由AB＝A（En，B(→)1）＝0，知AEn＝0，故A＝0。

  • 第11题：

    填空题
    设A为n阶方阵，若对任意n×m（m≥n）矩阵B都有AB=0，则A=____.

    正确答案： 0
    解析：
    取基本单位向量组为ε1，ε2，…εn
    当m=n时，由对任意B都有AB=0，则对B=（ε1，ε2，…εn）=En也成立，即AE=0，故A=0．
    当m>n时，取B=（ε1，ε2，…εn，B1）=（En，B1），则由AB=A（En，B1）=0，知AEn=0，故A=0．

  • 第12题：

    单选题
    下列结论中正确的是（    ）
    A

    矩阵A的行秩与列秩可以不等

    B

    秩为r的矩阵中，所有r阶子式均不为零

    C

    若n阶方阵A的秩小于n，则该矩阵A的行列式必等于零

    D

    秩为r的矩阵中，不存在等于零的r-1阶子式


    正确答案： D
    解析：

  • 第13题：

    若A,B均为n阶方阵,则当|A|>|B|时，A,B一定不相似


    答案：对
    解析：
    正确，因为相似矩阵必须有相同特征值和行列式

  • 第14题：

    设n阶矩阵A与对角矩阵相似,则().

    A.A的n个特征值都是单值
    B.A是可逆矩阵
    C.A存在n个线性无关的特征向量
    D.A一定为n阶实对称矩阵

    答案：C
    解析：
    矩阵A与对角阵相似的充分必要条件是其有n个线性无关的特征向量，A有n个单特征值只是其可对角化的充分而非必要条件，同样A是实对称阵也是其可对角化的充分而非必要条件，A可逆既非其可对角化的充分条件，也非其可对角化的必要条件，选(C).

  • 第15题：

    若n阶矩阵A，B有共同的特征值，且各有n个线性无关的特征向量，则（ ）

    A.A与B相似
    B.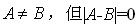
    C.A=B
    D.A与B不一定相似，但|A|=|B|


    答案：A
    解析：

  • 第16题：

    设A与B都是n阶方阵,且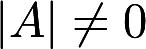,证明AB与BA相似.


    答案：
    解析：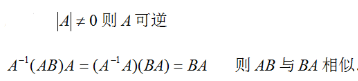

  • 第17题：

    设A是三阶矩阵，已知 ，B与A相似，则B的相似对角形为


    答案：
    解析：

  • 第18题：

    设A为n阶方阵，A*是A的伴随矩阵，则||A|A*|等于（ ）.



    答案：D
    解析：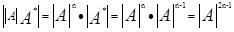

  • 第19题：

    若一个n阶矩阵A中的元素满足：Aij=Aji（0<=I，j<=n-1）则称A为（）矩阵；若主对角线上方（或下方）的所有元素均为零时，称该矩阵为（）。


    正确答案:上；三角矩阵

  • 第20题：

    填空题
    设A、B、C均为n阶方阵，若A＝CTBC，且|B|＜0，则|A|____。

    正确答案： ≤0
    解析：
    由行列式性质可知|A|＝|CT|·|B|·|C|＝|C|2·|B|≤0。

  • 第21题：

    填空题
    设A为n阶方阵，E为n阶单位矩阵，且A2＝A，则（A－2E）－1＝____。

    正确答案： -(A+E)/2
    解析：
    由题设A2＝A有，A2－A－2E＝（A－2E）（A＋E）＝－2E，即（A－2E）[－（A＋E）/2]＝E，所以有（A－2E）－1＝－（A＋E）/2。

  • 第22题：

    单选题
    设A为n阶方阵，A*是A的伴随矩阵，则||A|A*|等于（　　）。
    A

    ｜A｜2

    B

    ｜A｜n

    C

    ｜A｜2n

    D

    ｜A｜2n－1


    正确答案： D
    解析：
    ||A|A*|＝|A|n·|A*|＝|A|n·|A|n－1＝|A|2n－1。

  • 第23题：

    单选题
    设A为n阶方阵，B是A经过若干次矩阵的初等变换后所得到的矩阵，则有（　　）。
    A

    ｜A｜＝｜B｜

    B

    ｜A｜≠｜B｜

    C

    若｜A｜＝0，则一定有｜B｜＝0

    D

    若｜A｜＞0，则一定有｜B｜＞0


    正确答案： A
    解析：
    矩阵A经过若干次初等变换后得到矩阵B，则存在可逆矩阵P，Q使得B＝PAQ，因此|B|＝|PAQ|＝|P|·|A|·|Q|，若|A|＝0，则必有|B|＝|P|·|A|·|Q|＝0成立。

  • 第24题：

    填空题
    若一个n阶矩阵A中的元素满足：Aij=Aji（0<=I，j<=n-1）则称A为（）矩阵；若主对角线上方（或下方）的所有元素均为零时，称该矩阵为（）。

    正确答案： 上,三角矩阵
    解析： 暂无解析

相关内容