一个3元线性方程组只有一个解，则系数矩阵与增广矩阵的主元列数分别为A．0，0B．3，0C．0，3D．3，3

题目

一个3元线性方程组只有一个解，则系数矩阵与增广矩阵的主元列数分别为

A．0，0

B．3，0

C．0，3

D．3，3

相似考题

1.若A是____,则A必为方阵。A.对称矩阵B.可逆矩阵C.n阶矩阵的转置矩阵D.线性方程组的系数矩阵

2.如果线性方程组的系数矩阵满秩则该方程组一定有解且解是唯一的。()此题为判断题(对，错)。

3.矩阵A是m×n矩阵,齐次线性方程组AX=0只有零解的充要条件是A的列向量线性无关。()此题为判断题(对，错)。

4.如果线性方程组的系数矩阵满秩,则该方程组一定有解组,且解是唯一的。()此题为判断题(对，错)。

更多“一个3元线性方程组只有一个解，则系数矩阵与增广矩阵的主元列数分别为”相关问题

  • 第1题：

    如下是一个稀疏矩阵的三元组法存储表示和相关的叙述

    行下标

    列下标

    值

    1

    1

    3

    1

    4

    5

    2

    3

    2

    3

    2

    6

    3

    4

    5

    5

    3

    3

    I．该稀疏矩阵有5行

    II．该稀疏矩阵有4列

    III．该稀疏矩阵有6个非0元素

    这些叙述中哪个（些）是正确的？

    A．只有I

    B．I和II

    C．只有III

    D．I、II和III


    正确答案：C

  • 第2题：

    什么是线性方程组的系数矩阵和增广矩阵?


    参考答案：系数矩阵：方程组左边各方程的系数作为矩阵就是此方程的系数矩阵。增广矩阵：将非齐次方程右边作为列向量加在系数矩阵后就是增广矩阵。

  • 第3题：

    若采用邻接矩阵法存储一个n个顶点的无向图，则该邻接矩阵是一个( )。

    A．上三解矩阵

    B．稀疏矩阵

    C．对角矩阵

    D．对称矩阵


    正确答案：D
    解析：在邻接矩阵来表示的图中，从一个点到另一个点的边，则相应位置上为1，否则为1，由于是无向图，点a到b存在边，那么点b到a也存在边，因此表示出来的邻接矩阵为对称矩阵。

  • 第4题：

    设A为矩阵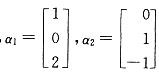，都是线性方程组Ax=0的解，则矩阵A为：


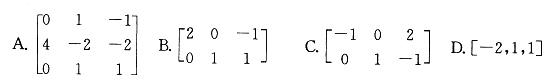    答案：D
    解析：
    提示：a1，a2是方程组Ax=0的两个线性无关的解，方程组含有3个未知量，帮矩阵A的秩R（A）=3-2=1，而选项A、B、C的秩分别为3、2、2，均不符合要求。将选项D代入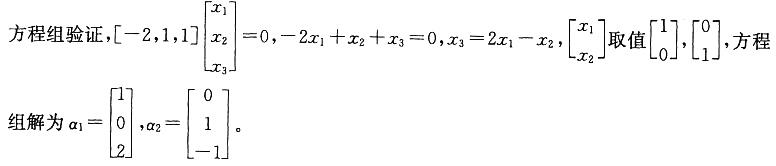

  • 第5题：

    设有三张不同平面的方程 ,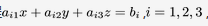 ,它们所组成的线性方程组的系数矩阵与增广矩阵的秩都为２,则这三张平面可能的位置关系为



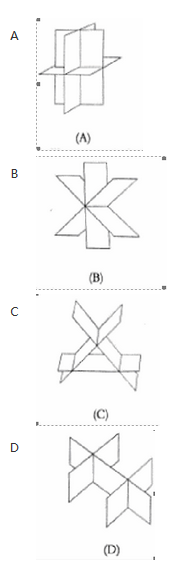    答案：B
    解析：

  • 第6题：

    设A，B为n阶矩阵，考虑以下命题：①若A，B为等价矩阵，则A，B的行向量组等价②若行列式.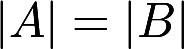，则A，B为等价矩阵③若与都只有零解，则A，B为等价矩阵④若A，B为相似矩阵，则与的解空间的维数相同以上命题中正确的是（ ）.

    A.①③
    B.②④
    C.②③
    D.③④

    答案：D
    解析：

  • 第7题：

    设A为m×n矩阵，则齐次线性方程组Ax＝0有非零解的充分必要条件是（　　）。

    A、矩阵A的任意两个列向量线性相关
    B、矩阵A的任意两个列向量线性无关
    C、矩阵A的任一列向量是其余列向量的线性组合
    D、矩阵A必有一个列向量是其余列向量的线性组合

    答案：D
    解析：

  • 第8题：

    利用逆矩阵，解线性方程组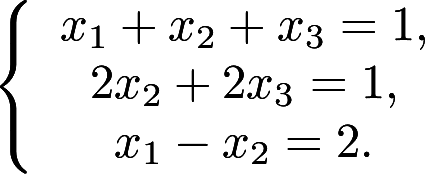


    答案：
    解析：

  • 第9题：

    关于LP的基的说法不正确的是（）。

    • A、基是约束方程系数矩阵中的一个子矩阵
    • B、基解中非零值的个数大于等于约束方程数
    • C、基中的每一个列向量称为基向量
    • D、与基向量对应的变量称为基变量

    正确答案:B

  • 第10题：

    一个ROM的存储矩阵有64行、64列，则存储矩阵的存储容量为（）个存储（）。


    正确答案:216；元

  • 第11题：

    单选题
    设A是4×6矩阵，则齐次线性方程组AX=0解的情况是（）。
    A

    无解

    B

    只有零解

    C

    有非零解

    D

    不一定


    正确答案： A
    解析： AX=0有非零解的充要条件是R（A）＜6，而4×6矩阵的秩R（A）≤4，故AX=0有非零解，故选（C）。

  • 第12题：

    单选题
    n元线性方程组AX(→)＝b(→)有唯一解的充要条件为（　　）。
    A

    A为方阵且｜A｜≠0

    B

    导出组AX(→)＝0(→)仅有零解

    C

    秩（A）＝n

    D

    系数矩阵A的列向量组线性无关，且常数向量b(→)与A的列向量组线性相关


    正确答案： C
    解析：
    A项，系数矩阵A不一定是方阵；B项，导出组只有零解，方程组AX(→)＝b(→)不一定有解；C项，当r（A）＝n时，不一定有r（A）＝r（A(＿)）＝n；D项，b(→)可由A的列向量组线性表示，则方程组AX(→)＝b(→)有唯一解。

  • 第13题：

    用迭代法解线性方程组时，迭代能否收敛与初始向量的选择、系数矩阵及其演变方式有关，与常数项无关。()


    参考答案：×

  • 第14题：

    用高斯顺序消去法解线性方程组，消元能进行到底的充分必要条件是线性方程组的系数矩阵的各阶顺序主子式均不为0()


    参考答案：√

  • 第15题：

    如下是一个稀疏矩阵的三元组法存储表示和相关的叙述：

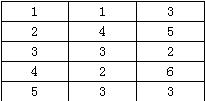
    ①该稀疏矩阵有5行

    ②该稀疏矩阵有4列

    ③该稀疏矩阵有6个非0元素

    这些叙述中哪个(些)是正确的? ( )

    A．只有①

    B．①和②

    C．只有③

    D．①、②和③


    正确答案：B

  • 第16题：

    若A是m×n矩阵，且m≠n，则当R（A）=n时，齐次线性方程组AX=0只有零解


    答案：对
    解析：

  • 第17题：

    设n阶矩阵A的伴随矩阵A^*≠0，若ζ1，ζ2，ζ3，ζ4是非齐次线性方程组Ax=b的互不相等的解，则对应的齐次线性方程组Ax=0的基础解系

    A.不存在.
    B.仅含一个非零解向量.
    C.含有两个线性无关的解向量.
    D.含有三个线性无关的解向量.

    答案：B
    解析：

  • 第18题：

    设n元齐次线性方程组Ax=0的系数矩阵A的秩为r，则Ax=0有非零解的充要条件为（ ）。

    A.r=n
    B.r＜n
    C.r≥n
    D.r＞n

    答案：B
    解析：
    Ax=0有非零解的充要条件为｜A｜=0，即矩阵A不是满秩的，r＜n。

  • 第19题：

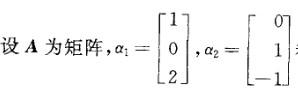    都是线性方程组Ax=0的解，则矩阵A为:


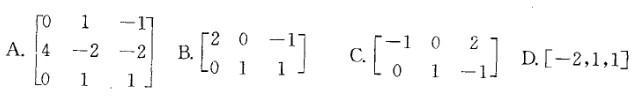    答案：D
    解析：
    提示:a1,a2是方程组Ax=0的两个线性无关的解，方程组含有3个未知量，故矩阵A的秩R(A)=3-2=1，而选项A、B、C的秩分别为3、2、2均不符合要求。将选项D代入方程组_

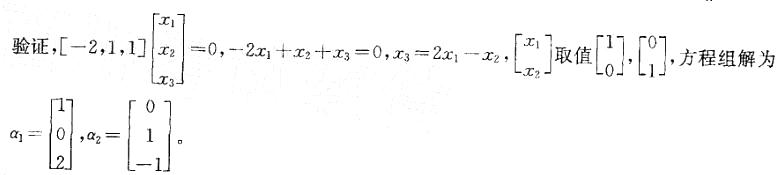  • 第20题：

    设A为矩阵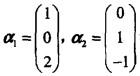，都是齐次线性方程组Ax=0的解，则矩阵A为( )。



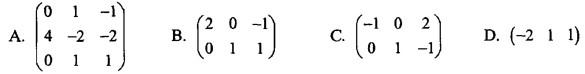    答案：D
    解析：
    提示：由于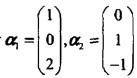线性无关，故R(A)= 1，显然选项A中矩阵秩为3,选项B和C中矩阵秩都为2。

  • 第21题：

    下列关于品牌与产品矩阵，描述正确的是（）。

    • A、品牌与产品矩阵反映了一个公司拥有的全部品牌和产品
    • B、矩阵的一行就是一个品牌线
    • C、矩阵的一列就是一个产品线
    • D、矩阵的列代表产品-品牌的关系及品牌组合战略

    正确答案:A,B,C,D

  • 第22题：

    设A是4×6矩阵，则齐次线性方程组AX=0解的情况是（）。

    • A、无解
    • B、只有零解
    • C、有非零解
    • D、不一定

    正确答案:C

  • 第23题：

    单选题
    设A为m×n矩阵，则齐次线性方程组Ax＝0有非零解的充分必要条件是（　　）。[2017年真题]
    A

    矩阵A的任意两个列向量线性相关

    B

    矩阵A的任意两个列向量线性无关

    C

    矩阵A的任一列向量是其余列向量的线性组合

    D

    矩阵A必有一个列向量是其余列向量的线性组合


    正确答案： D
    解析：
    线性方程组Ax＝0有非零解⇔|A|＝0⇔r（A）＜n，矩阵A的列向量线性相关，所以矩阵A必有一个列向量是其余列向量的线性组合。

  • 第24题：

    单选题
    求解线性方程组的高斯主元消去法的条件为（　）。
    A

    三对角矩阵

    B

    上三角矩阵

    C

    对称正定矩阵

    D

    各类大型稀疏矩阵


    正确答案： A
    解析： 暂无解析

相关内容