若阶码为3位，用补码表示；尾数7位，用原码表示，其中1位为符号位；以2为底。数据格式为：尾数符号 阶符符号 阶码值 尾数值，则十进制数27/64的浮点规格化数是（）（单选）A．010*******B．010*******C．0111110110D．0001011011

题目

若阶码为3位，用补码表示；尾数7位，用原码表示，其中1位为符号位；以2为底。数据格式为：尾数符号 阶符符号 阶码值 尾数值，则十进制数27/64的浮点规格化数是（）（单选）

A．010*******

B．010*******

C．0111110110

D．0001011011

相似考题

1.设某浮点数共12位，其中阶码含1位阶符共4位，以2为底，补码表示；尾数含1位数符共8位，补码表示，则规格化浮点数所能表示的最大正数是A.26-1B.27-1C.28-1D.29-1

2.计算机内采用规格化浮点数表示，阶码用移码表示(最高位代表符号位)，尾数用原码表示。(1)表示不是规格化浮点数。 阶码 尾数A．1111111 1.1000......00B．0011111 1.0111......01C．1000001 0.1111......01D．0111111 0.1000......10

3.设机器中浮点数的格式如下：其中阶码6位，包括1位符号位，尾数10位(含1位数符)，浮点数的基为2。阶码用补码表示，尾数用原码表示。对于十进制数-25.8375，当阶码用补码表示、尾数用原码表示时，得到的规格化机器码为(38)；当阶码用移码表示、尾数用原码表示时，得到的规格化机器码为(39)；当阶码用原码表示，尾数用补码表示时，得到的规格化机器码为(40)。A．1001011100111000B．1110101100111010C．1001011000111010D．1001011100111010

4.二进制浮点数补码表示为49AH,前4位阶码,后8位尾数,符号位均为1位,试问真值十进制数为多少?写出计算步骤。

更多“若阶码为3位，用补码表示；尾数7位，用原码表示，其中1位为符号位；以2为底。数据格式为：尾数符号 阶符符号 阶码值 尾数值，则十进制数27/64的浮点规格化数是（）（单选）”相关问题

  • 第1题：

    设浮点数字长16位，其中阶码5位(含1位阶符)，以2为底补码表示，尾数11位(含1位数符)补码表示，下列十进制数表示成规格化浮点数为多少?

    设浮点数字长16位,其中阶码5位(含1位阶符),以2为底补码表示,尾数11位(含1位数符)补码表示,下列十位进制数表示成规化浮点数为多少?

    3.5：(1)；79/512：(2)；-10-4：(3)；1010：(4)

    A．不能表示成浮点数

    B．11110 01001111000

    C．10010 01110000000

    D．11101 10111111110


    正确答案：C

  • 第2题：

    用8位寄存器表示浮点数，左3位为阶码(含1位符号)，右5位为尾数(含1尾符)，阶码用移码，尾数用补码表示时，(-3.25)10的浮点数形式是(1)。

    A．

    B．

    C．

    D．


    正确答案：A
    解析：(-3.25)10=-0.1101×2+2，阶码2用移码表示为110，尾数-0.1101用补码表示为10011，所以选A。

  • 第3题：

    某计算机系统中，16位浮点数的表示格式如图6-1所示。其中阶码4位(含1位符号)为定点整数，尾数12位(含1位符号)为定点小数，设一个数机器码为1110001010000000。

    若阶码为移码且尾数为原码，则其十进制数真值为(2)；若阶码为补码且尾数为补码，则其十进制数真值规格化后的机器码为(3)。

    A．20

    B．25

    C．0.078125

    D．20.969375


    正确答案：A

  • 第4题：

    计算机中16位浮点数的表示格式如图1所示：

    某机器码为1110001010000000。

    若阶码为移码且尾数为反码，其十进制真值为(8)；

    若阶码为移码且尾数为原码，其十进制真值为(9)；

    若阶码为补码且尾数为反码，其十进制真值为(10)；

    若阶码为补码且尾数为原码，其十进制真值为(11)，将其规格化后的机器码为(12)。

    A．0.078125

    B．1.45

    C．20

    D．20.697395


    正确答案：C
    解析：本题考查计算机数据的编码，涉及原码、补码、反码和移码以及浮点数规格化处理。同一个数可以有不同的浮点表示形式，阶码的大小可以用来调节数值中小数点的位置。将数值数据表示成N=M+RE，M被称为N的尾数，E是N的指数或称阶码，而只是该阶码的基数。题中阶码用4位二进制整数1110表示，尾数用12位二进制小数001010000000表示，尾数中含有符号位，其最高位即符号位为0。下面具体解答各个问题。(8)如果阶码为移码，由于阶码是4位二进制整数，设真值为X，根据整数移码定义：[X]移码=23+X=(1110)2=(14)10，可此求得阶码真值为6。如果尾数为反码，从符号为可判断尾数是正数，根据小数反码定义，正小数的反码就是其自身，可求得尾数的真值为：(0.01010000000)2=(2-2+2-4)=(0.3125)10，根据浮点数定义，该机器码真值为0.3125+26=20。(9)如果阶码为移码，同上，真值为6。如果尾数是原码，从符号位可判断尾数是正数，根据小数原码定义，正小数的原码就是其本身，可求得尾数的真值位0.3125。这样该机器码的真值也是20。(10)如果阶码为补码，由于阶码是4位二进制整数，从符号位判断为负数，设真值为X，根据负整数定义[X]补码=24+x=(1110)2=(14)10，求得阶码的真值为-2。如果尾数为反码，同问题(8)一样求出尾数的真值为0.3125。这样，该机器码真值为0.3125*2-2=0.078125。(11)如果阶码是补码，尾数是原码，可分别参照问题(10)和问题(9)求出阶码和尾数的真值分别为-2和0.3125这样该机器码的真值也是0.078125。(12)这是对浮点数进行规格化处理。规定浮点数的尾数部分用纯小数形式表示，当尾数的值不为0时，其绝对值应大于或等于0.5，用二进制表示为0.1xxx…xx(x为0或1)。对于不符合这一规定的浮点数。可采用改变阶码的大小并同时左右移尾数的方法来满足这一规定。显然尾数0.01010000000不符合要求，应左移1位，而阶码则相应地减1，因此规格化处理后的阶码为1101，尾数为010100000000。

  • 第5题：

    ●计算机中十六位浮点数的表示格式为

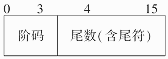
    某机器码为1110001010000000，

    若阶码为移码且尾数为反码，则其十进制真值为 (7) ；

    若阶码为移码且尾数为原码，则其十进制真值为 (8) ；

    若阶码为补码且尾数为反码，则其十进制真值为 (9) ；

    若阶码为补码且尾数为原码，则其十进制真值为 (10) ，将其规格化后的机器码为 (11) 。

    (7)～(10) A．0.078125

    B．20

    C．20.969375

    D．1.25

    (11) A．11110101000000

    B．1110001010000000

    C．1101010100000000

    D．11110001010000


    正确答案：B,B,A,A,C
    【解析】(7)如果阶码为移码，由于阶码是4位二进制整数，设真值为X，根据整数移码定义：［X］移码=23+X(1110)2=(14)10，可求得阶码真值为6。如果尾数为反码，从符号位可判断尾数是正数，根据小数反码定义，正小数的反码就是其自身，可求得尾数的真值为：(0.01010000000)2=(2-2+2-4)=(0.3125)10，根据浮点数定义，该机器码真值为0.3125*26=20。(8)如果阶码为移码，同上，真值为6。如果尾数是原码，从符号位可判断尾数是正数，根据小数原码定义，正小数的原码就是其本身，可求得尾数的真值为0.3125。由此可知该机器码真值也是20。(9)如果阶码为补码，由于阶码是4位二进制整数，从符号位判断为负数，设真值为X，根据负整数定义［X］补码=24+X=(1110)2=(14)10，求得阶码的真值为-2。如果尾数为反码，同(7)一样求出尾数的真值为0.3125。这样，该机器码真值为0.3125*2-2=0.078125。(10)如果阶码是补码，尾数是原码，求出阶码和尾数的真值分别为-2和0.3125，这样该机器码的真值也是0.078125。(11)对浮点数进行规格化处理，规定浮点数的尾数部分用纯小数形式表示，当尾数的值不为0时，其绝对值应大于或等于0.5，用二进制表示为0.1XXX…XX(X为0或1)。对于不符合这一规定的浮点数，可改变阶码的大小并同时用左右移尾数的方法来满足这一规定。显然尾数0.01010000000不合要求，应左移1位，而阶码则应相应地减1，因此规格化处理后的阶码为1101，尾数为010100000000。

  • 第6题：

    计算机中十六位浮点数的表示格式为图1.4

    某机器码为1010001010000000。

    若阶码为移码且尾数为反码，则其真值为(60)；

    若阶码为移码且尾数为原码，则其真值为(61)；

    若阶码为补码且尾数为反码，则其真值为(62)；

    若阶码为补码且尾数为原码，则其真值为(63)，将其规格化后的机器码为(64)。

    A．0.00000001012

    B．2010

    C．1.2510

    D．20.96937510


    正确答案：C

  • 第7题：

    表示成如下浮点数格式，用十六进制表示正确的是：(1)表示尾数：原码、小数、24位，包括一个隐藏位；阶码：移码、整数、7位：阶码和尾数均不包括符号位，基值均为2。(2)表示尾数：基值为16、原码、小数、6位；阶码：基值为2、移码、整数、6位；阶码和尾数均不包括符号位。

    A．3ECCCCCC

    B．40199999

    C．3ECCCCCE

    D．40lA0000

    E．3ECCCCCD


    正确答案：A
    解析：(1)尾符阶码隐藏位尾数001111101110011001100110011001100写成16进制规格化浮点数格式为：3ECCCCCC

  • 第8题：

    在浮点表示法中，用阶码和尾数表示一个浮点数。阶码通常为( ) 纯整数，尾数为带符号的纯小数。

    A.不带符号
    B.带符号
    C.取绝对值
    D.不确定

    答案：B
    解析：
    浮点数由两部分组成，第一部分是指数部分，表示小数点浮动的位置；第二部分是尾数部分，表示数的符号和有效位数。

  • 第9题：

    设16位浮点数，其中阶符1位、阶码值6位、数符1位、尾数8位。若阶码用移码表示，尾数用补码表示，则该浮点数所能表示的数值范围是（ ）。



    答案：B
    解析：

  • 第10题：

    某浮点机字长16位，其中，阶码5位(含1位阶符)，采用补码表示，基数为4；尾数儿位(含1位数符)，采用补码表示，且为规格化形式，则其可以表示的最小正数是()。


    答案：C
    解析：

  • 第11题：

    设16位浮点数，其中阶符1位、阶码值6位、数符1位，尾数8位。若阶码用移码表示，尾数用补码表示，则该浮点数所能表示的数值范围是（ ） 。

    A.-2^64~(1-2^-8)^64
    B.-2^63~(1-2^-8)^63
    C.-(1-2^-8)2^64~(1-2^-8)2^64
    D.-(1-2^-8)2^63~(1-2^-8)2^63

    答案：B
    解析：
    阶和尾数分别带着符号位表示，依次为阶符(ES)、阶(E)、数符(MS)和尾数(M) 也有另一种表示形式，将数符移到最前面表示。 最大规格化尾数：1 - 2-m;最大阶码：2p– 1;8位字长补码表示的有符号定点小数范围: -1.0000000b+ ～ 0.1111111b 即: -1d ～ +（127/128）d

  • 第12题：

    问答题
    设某浮点数格式为：字长12位，阶码6位，用移码表示，尾数6位，用原码表示，阶码在前，尾数（包括数符）在后，则按照该格式：已知X=-25/64，Y=2.875，求数据X、Y的规格化的浮点数形式。

    正确答案： [X]=-0.011001=-0.11001*2-1
    X.的符号：1
    X.的阶码：-1=-00001=（移码）011111
    X.的尾数：11001
    解析： 暂无解析

  • 第13题：

    设阶码8位(最左一位为符号位)，用移码表示，尾数为24位(最左一位为符号位)，用规格化补码表示，则它所能表示的最大正数的阶码为(27)，尾数为(28)；绝对值最小的负数的阶码为(29)，尾数为(30)。

    A．11110000

    B．11111111

    C．1111

    D．0


    正确答案：B

  • 第14题：

    计算机中十六位浮点数的表示格式为

    某机器码为1110001010000000，

    若阶码为移码且尾数为反码，则其十进制真值为(7)；

    若阶码为移码且尾数为原码，则其十进制真值为(8)；

    若阶码为补码且尾数为反码，则其十进制真值为(9)；

    若阶码为补码且尾数为原码．则其十进制真值为(10)，将其规格化后的机器码为(11)。

    A．0.078125

    B．20

    C．20.969375

    D．1.25


    正确答案：B
    解析：(7)如果阶码为移码，由于阶码是4位二进制整数，设真值为X，根据整数移码定义：[X]移码=23+X(1110)2=(14)10，可求得阶码真值为6。如果尾数为反码，从符号位可判断尾数是正数，根据小数反码定义，正小数的反码就是其自身，可求得尾数的真值为：(0.01010000000)2=(2-1+2-4)=(0.3125)10，根据浮点数定义，该机器码真值为0.3125*26=20。(8)如果阶码为移码，同上，真值为6。如果尾数是原码，从符号位可判断尾数是正数，根据小数原码定义，正小数的原码就是其本身，可求得尾数的真值为0.3125。由此可知该机器码真值也是20。(9)如果阶码为补码，由于阶码是4位二进制整数，从符号位判断为负数，设真值为X，根据负整数定义[X]补码=24+X=(1110)2=(14)10，求得阶码的真值为-2。如果尾数为反码，同(7)一样求出尾数的真值为0.3125。这样，该机器码真值为0.3125*2-2=0.078125。(10)如果阶码是补码，尾数是原码，求出阶码和尾数的真值分别为-2和0.3125，这样该机器码的真值也是0.078125。(11)对浮点数进行规格化处理，规定浮点数的尾数部分用纯小数形式表示，当尾数的值不为0时，其绝对值应大于或等于0.5，用二进制表示为0.1XXX…XX(X为0或1)。对于不符合这一规定的浮点数，可改变阶码的大小并同时用左右移尾数的方法来满足这一规定。显然尾数0.01010000000不合要求，应左移1位，而阶码则应相应地减1，因此规格化处理后的阶码为1101，尾数为010100000000。

  • 第15题：

    下面是机器中浮点数的表示格式：

    设浮点数的基为2。若阶码用补码表示、尾数用原码表示，十进制数-51.875采用上述格式可表示为(7)；若阶码用移码表示、尾数用补码表示，该数可表示为(8)。

    A．0110 111001111100

    B．0110 011001111100

    C．0110 001110011111

    D．0101 011001111100


    正确答案：A
    解析：首先将-51.875转换为二进制表示：(-51.875)10=-110011.111=-0.110011111×2110，其中110是阶码，-0.110011111是尾数(绝对值大于0.5)。由于规格化表示格式中阶符和阶码共计4位，本题中阶码大于0，故采用补码时，这4位应该是[110]补=[110]原=0110。而采用原码表示尾数时，向[-0.110011111]原=1110011111后面添零补足12位，得111001111100。

  • 第16题：

    用12位寄存器表示规格化浮点数，左4位为阶码(含1位符号)，右8位为尾数(含1尾符)，阶码用移码，尾数用补码表示时，(-40)10表示成规定的浮点数是(2)。

    A．

    B．

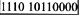
    C．

    D．


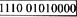    正确答案：B
    解析：浮点数中尾数最高位的真值为1的浮点数称为规格化浮点数。将浮点数规格化的方法是调整阶码使尾数满足下列关系：尾数为原码表示时，无论正负应满足1/2<|d|1，即小数点后的第一位数一定要为1。正数的尾数应为0.1x…x，负数的尾数应为1.1x…x。尾数用补码表示时，小数最高位应与数符符号位相反。正数应满足1/2d1，即0.1x…x；负数应满足-1/2＞d－1，即1.0x…x。(-40)10=-(0.101000)2×2+6，阶码6用移码表示为1110，尾数-0.101000用补码表示为1011000，尾数为8位所以加补一位0，因此选B。

  • 第17题：

    某计算机系统中，16位浮点数的表示格式如图6-1所示。其中，阶码4位(含1位符号)为定点整数，尾数12位(含1位符号)为定点小数。

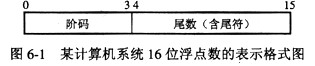
    设一个数机器码为1110001010000000，若阶码为移码且尾数为原码，则其十进制数真值为(1)。

    A．20

    B．25

    C．0.078125

    D．20.969375


    正确答案：A
    解析：为了充分利用尾数来表示更多的有效数字，即提高数据的表示精度，通常采用规格化浮点数。规定化浮点数在运算结束将运算结果存到计算机中时，必须是规格化的浮点数。规格化浮点数尾数的最高数值位是有效数字，即正尾数0.5≤F1，负尾数-1F≤-0.5。要求规格化以后，其尾数部分是正数时为0.1×××的形式，是负数时，对于原码为1.1×××的形式，对于补码为1.0×××的形式，可以通过尾数小数点的左右移动和阶码的变化实现。对于本试题的解答思路是，对给定的机器码按给定的浮点数格式得到阶码和尾数，然后将阶码变为十进制数，最后得到浮点数的十进制真值。判断如果给定的浮点数机器码不是规格化表示的，则可将其表示为规格化的机器码。规格化时，先看给定的浮点数机器码的尾数是用什么码表示的，然后看看是否已是规格化数，如不是，将尾数小数点移位，但要注意，为保持浮点数的真值不变，阶码一定要相应地调整。另外在解答此类题目时，还要注意题目条件中给出的阶码和尾数是用什么码表示的，否则很容易出错，而得不到正确的计算结果。针对本道题目，对所给机器码1110001010000000，按所规定的浮点数表示形式，可知阶码为1110(最高位为阶符1)，尾数为001010000000(最高位为尾符0)。①若阶码为移码，1110表示为十进制数加6，尾数为原码表示加0.010lB，所以浮点数为26×0.0101B=010100B=20。②若阶码为补码，1110表示为十进制数减2；尾数为补码，因该尾数为正数，即加0.0101，该浮点数为2-2×0.0101B=0.000101B=0.078125D。将此浮点数用规格化数形式表示：2-2÷0.0101B=2-3×0.101B，阶码-3的补码为1101，因为浮点数规格化要求尾数最高数据位为有效数据位，即尾数绝对值大于等于0.5。实际判断中，对于尾数以补码表示时，看符号位与最高位是否相同，如不相同即为规格化数，如相同即为非规格化数，故规格化后的机器码为1101010100000000。对本题所给出的机器码来说，就是使其尾数001010000000左移一位成为010100000000，相当于尾数数值乘2，相应地其阶码就应减1，即-2减1得-3。

  • 第18题：

    下面是某种计算机的32位短浮点数格式如图1.7

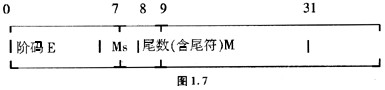
    其中，M为用定点小数表示的尾数的绝对值，占23位；Ms是尾数的符号位，占1位；Ms和M一起表示尾数。E为用定点整数表示的阶码，占8位。若机器表示中取阶码的基数为2，求采用下列五种不同编码方式时，浮点数-123625E-3(隐含基数为10)规格化后的机器码：

    阶码用补码方式、尾数用原码方式时，为(80)；

    阶码用补码方式、尾数用反码方式时，为(81)；

    阶码用移码方式、尾数用原码方式时，为(82)；

    阶码用移码方式、尾数用补码方式时，为(83)；

    阶码用移码方式、尾数用反码方式时，为(84)；

    A．10000111100001000110000000000000

    B．00000111100001000101111111111111

    C．10000111111110000101111111111111

    D．00000111111110111010000000000000


    正确答案：D

  • 第19题：

    某浮点数格式如下：7位阶码（包含一个符号位），9位尾数（包含一个符号位）。若阶码用移码、尾数用规格化的补码表示，则浮点数所能表示数的范围是（ ）。

    A.-263～(1-2-8)×263 B.-264～(1-2-7)×264 C.-(1-2-8)×263 ～263 D.-(1-2-7)×264～(1-2-8)×263


    正确答案：A

  • 第20题：

    设32位浮点数格式如下。以下关于浮点数表示的叙述中，正确的是（ ）。若阶码采用补码表示，为8位（含1位阶符），尾数采用原码表示，为24位（含1位数符），不考虑规格化，阶码的最大值为（请作答此空）。

    A.255
    B.256
    C.127
    D.128

    答案：C
    解析：
    本题考察计算机数据的表示。浮点数所能表示的数值范围主要由阶码决定，所表示数值的精度则由尾数决定。八位阶码的最大值为127。

  • 第21题：

    若浮点数用原码表示，则判断运算结果为规格化数的方法是()。

    A.阶符与数符相同
    B.阶符与数符相异
    C.尾数最高数值位为1
    D.尾数符号与尾数最高数值位不相同

    答案：C
    解析：
    为了提高浮点数的精度，其尾数必须为规格化数，当基数为2时，尾数最高位为l的数为规格化数。题干中浮点数用原码表示与真值的二进制表示之间只是符号位表示上的不同。

  • 第22题：

    某浮点数格式如下：7 位阶码（包含一个符号位），9 位尾数（包含一个符号位）。若阶码用移码、尾数用规格化的补码表示，则浮点数所能表示数的范围是（）。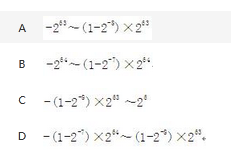


    答案：A
    解析：
    浮点数所能表示的数值范围如下：最大的正数

  • 第23题：

    设16位浮点数，其中阶符1位、阶码值6位、数符1位，尾数8位。若阶码用移码表示，尾数用补码表示，则该浮点数所能表示的数值范围是（3） 。


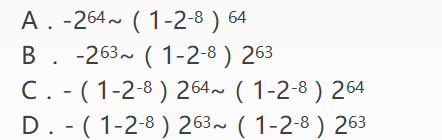    A.A
    B.B
    C.C
    D.D

    答案：B
    解析：

  • 第24题：

    单选题
    下列关于IEEE 754浮点数格式的叙述中，正确的是（　　）。
    A

    尾数和阶码均用原码表示

    B

    尾数用补码表示、阶码用原码表示

    C

    只能表示规格化数

    D

    可以表示规格化数和非规格化数


    正确答案： C
    解析：
    IEEE 754的浮点格式既可以表示规格化数，也可以表示非规格化数，同时，指数部分采用移码表示，尾数部分采用原码表示。

相关内容