旋转曲面:x2 -y2-z2=1是下列哪个曲线绕何轴旋转所得？ A. xOy平面上的双曲线绕x轴旋转所得 B. xOz平面上的双曲线绕z轴旋转所得 C. xOy平面上的橢圆绕x轴旋转所得 D. xOz平面上的椭圆绕x轴旋转所得

题目
旋转曲面:x2 -y2-z2=1是下列哪个曲线绕何轴旋转所得？
A. xOy平面上的双曲线绕x轴旋转所得
B. xOz平面上的双曲线绕z轴旋转所得
C. xOy平面上的橢圆绕x轴旋转所得
D. xOz平面上的椭圆绕x轴旋转所得

相似考题

1.设曲线y=f(x)上任一点(x，y)处的切线斜率为(y/x)+x2，且该曲线经过点（1，1/2）。（1）求函数y=f(x)；（2）求由曲线y= f(x），y=O，x=1所围图形绕x轴旋转一周所得旋转体的体积V。

2.由曲线和直线x=1，x=2，y= -1围成的图形，绕直线：y= -1旋转所得旋转体的体积为：

3.将椭圆绕x轴旋转一周所生成的旋转曲面的方程是:

4.将xoy面上的曲线y=x2绕y轴旋转一周所得旋转面的方程为()。

更多“旋转曲面:x2 -y2-z2=1是下列哪个曲线绕何轴旋转所得？ ”相关问题

  • 第1题：

    椭圆x2/a2+y2/b2=1(a>b>0)绕x轴旋转得到的旋转体体积V1与绕y轴旋转得到的旋转体体积V2之间的关系为：
    A.V1>V2 B.V1﹤V2 C.V1=V2 D.V1=3V2


    答案：B
    解析：
    提示:画出椭圆，分别计算该图形绕x轴、y轴旋转体的体积，通过计算V1=(4/3)ab2 ,V2 =(4/3)a2b，再比较大小。计算如下：

  • 第2题：

    将椭圆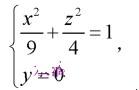绕χ轴旋转一周所生成的旋转曲面的方程是：


    答案：C
    解析：

  • 第3题：

    求曲线y=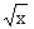，直线z=1和z轴所围成的有界平面图形的面积s，及该平面图形绕2轴旋转一周所得旋转体的体积V．


    答案：
    解析：


  • 第4题：

    求曲线y=x2与直线y=0，x=1所围成的平面图形绕x轴旋转一周所得旋转体的体积．


    答案：
    解析：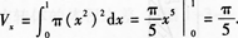

  • 第5题：

    ①求在区间(0，π)上的曲线y=sinx与x轴所围成图形的面积S；
    ②求①中的平面图形绕x轴旋转一周所得旋转体的体积Vx．


    答案：
    解析：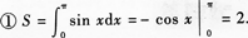

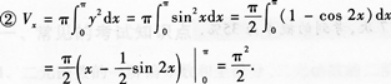
  • 第6题：

    设非负函数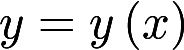满足微分方程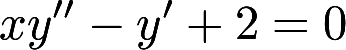，当曲线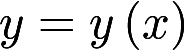过原点时，其与直线x=1及y=0围成平面区域D的面积为2，求D绕y轴旋转所得旋转体的体积


    答案：
    解析：

  • 第7题：

    将平面曲线y=x2分别绕y轴和x轴旋转一周，所得旋转曲面分别记作S1和S2。
    (1)在空间直角坐标系中，分别写出曲面S1和S2的方程；
    (2)求平面y=4与曲面S1。所围成的立体的体积。


    答案：
    解析：
    (1)在空间直角坐标系中，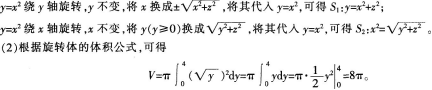

  • 第8题：

    求由曲线y2=(x-1)3和直线x=2所围成的图形绕x轴旋转所得的旋转体的体积.?


    答案：
    解析：

  • 第9题：



    (1)求曲线y=f(x)；
    (2)求由曲线y=f(x)，y=0，x=1所围图形绕x轴旋转一周所得旋转体体积．


    答案：
    解析：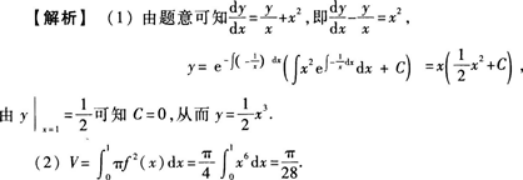

  • 第10题：

    CAXA制造J程师软件中关于旋转面建模方法描述错误的是（）。

    • A、旋转母线绕旋转轴线旋转可生成旋转曲面
    • B、构造旋转曲面的旋转轴必须是直线
    • C、构造旋转曲面的旋转母线可以是样条线
    • D、构造旋转曲面的旋转轴必须绘制在草图中

    正确答案:D

  • 第11题：

    由曲线与直线x=1及x轴所围图形绕y轴旋转而成的旋转体的体积是（）．

    • A、3/7π
    • B、4/7π
    • C、π/2
    • D、π

    正确答案:B

  • 第12题：

    单选题
    由曲线y=x2／2和直线x=1，x=2，y=-1围成的图形，绕直线y=-1旋转所得旋转体体积为：（）
    A

    （293／60）π

    B

    π／60

    C

    4π2

    D

    5π


    正确答案： D
    解析： 暂无解析

  • 第13题：

    将双曲线C：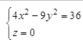

    绕x轴旋转一周所生成的旋转曲面的方程是（　　）。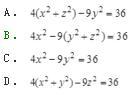


    答案：B
    解析：
    已知旋转曲面的母线C的方程为

    旋转轴为x轴，则只需将母线方程中的y换为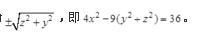

  • 第14题：

    将xoz坐标面上的双曲线




    分别绕z轴和x轴旋转一周，则所生成的旋转曲面的方程分别为( )。



    答案：A
    解析：
    绕z轴旋转所成的旋转曲面为旋转单叶双曲面，绕x轴旋转所成的旋转曲面为旋转双叶双曲面

  • 第15题：

    ①求曲线y=x2(x≥0)，y=1与x=0所围成的平面图形的面积S：
    ②求①中的平面图形绕Y轴旋转一周所得旋转体的体积Vy．


    答案：
    解析：
    ①由已知条件画出平面图形如图l—3-5阴影所示．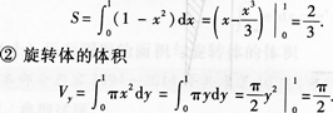

    图1—3—5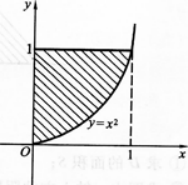

  • 第16题：

    设区域D={(x，y)（0≤y≤x2，0≤x≤1)，则D绕X轴旋转一周所得旋转体的体积为（）


    答案：A
    解析：
    【考情点拨】本题考查了旋转体的体积的知识点．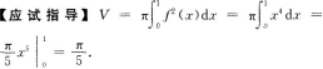

  • 第17题：

    求直线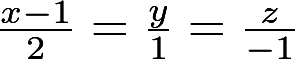 绕 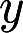轴旋转一周的旋转曲面的方程，并求该曲面与平面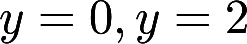所围立体的体积。


    答案：
    解析：

  • 第18题：

    （1）求直线y=1,曲线L以及y轴围成的平面图形绕y轴旋转一周所得到的的旋转体体积A；（2）假定曲线L绕y轴旋转一周所得到的旋转曲面为S。该旋转曲面作为容器盛满水（水的质量密度（单位体积水的重力）等于1），如果将其中的水抽完，求外力作功W.


    答案：
    解析：

  • 第19题：

    将双曲线，绕x轴旋转一周所生成的旋转曲面的方程是（ ）。


    答案：B
    解析：

  • 第20题：

    设D为曲线y=x2与直线y=x所围成的有界平面图形，求D绕x轴旋转一周所得旋转体的体积V.?


    答案：
    解析：

  • 第21题：

    由曲线y=x2／2和直线x=1，x=2，y=-1围成的图形，绕直线y=-1旋转所得旋转体体积为：（）

    • A、（293／60）π
    • B、π／60
    • C、4π2
    • D、5π

    正确答案:A

  • 第22题：

    旋转曲面x2-y2-z2=1是下列哪个曲线绕何轴旋转所得（）？

    • A、xOy平面上的双曲线绕x轴旋转所得
    • B、xOz平面上的双曲线绕z轴旋转所得
    • C、xOy平面上的椭圆绕x轴旋转所得
    • D、xOz平面上的椭圆绕x轴旋转所得

    正确答案:A

  • 第23题：

    单选题
    方程x2/2＋y2/2－z2/3＝0表示旋转曲面，它的旋转轴是（　　）。
    A

    x轴

    B

    y轴

    C

    z轴

    D

    直线x＝y＝z


    正确答案： C
    解析：
    由于选项中有三项均为坐标轴，可先考虑旋转轴是否为坐标轴，观察曲面方程x2/2＋y2/2－z2/3＝0中，x2，y2系数相等，则旋转轴应是z轴。（若三项系数均不相等，则应选D项）

相关内容