设f(x-1) =x2，则f(x+1)等于： A. (x-2)2 B. (x+2)2 C. x2-22 D.x2+22

题目
设f(x-1) =x2，则f(x+1)等于：
A. (x-2)2 B. (x+2)2 C. x2-22 D.x2+22

相似考题

1.设f(x)=ln(x＋1),则f(f(x))的定义域是多少?

2.设f(x)=3x,g(x)=x2，则函数g[f(x)]-f[g(x)]=_______________.

3.设f(x＋1)=x＋cos3x,则f(1)=()A、0B、1C、∏/2D、1+cos1

4.设x2为f(x)的一个原函数，则f(x)=_______

更多“设f(x-1) =x2，则f(x+1)等于： ”相关问题

  • 第1题：

    设f (x)=x2,g(x)=ex,则f [g(x)]=_________.


    正确答案：
    e2x

  • 第2题：

    设f(x)=则f{f［f(x)］)等于().


    答案：B
    解析：

  • 第3题：

    设f'(lnx) =1+x，则f(x)等于：
    A.lnx/2(2+lnx)+c B. x+1/2x2+c
    C. x+ex+c D. ex+1/2e2x+c


    答案：C
    解析：
    提示:设lnx=t，得f'(t)=1+et形式，写成f'(x) =1+ex ，积分。

  • 第4题：

    设 z=f(x2 - y2),则 dz 等于：(A) 2x-2y (B) 2xdx-2ydy (C) f (x2 - y2)dx (D) 2 f(x2 - y2)(xdx- ydy)


    答案：D
    解析：
    解：选D。函数求导的基本题目。

  • 第5题：

    设f(x)是周期为4的可导奇函数，且f'(x)=2(x-1)，x∈［0，2］，则f(7)=________.


    答案：1、1.
    解析：
    由f'(x)=2(x-1)，x∈［0，2］知，f(x)=(x-1)^2+C.又f(x)为奇函数，则f(0)=0,C=-1.f(x)=(x-1)^2-1.由于f(x)以4为周期，则f(7)=f［8+(-1)］=f(-1)=-f(1)=1.

  • 第6题：

    设f(x)具有二阶导数，y=f(x2),则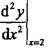的值为()。


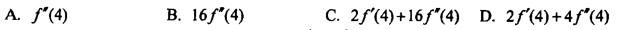    答案：C
    解析：
    正确答案是C。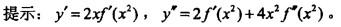

  • 第7题：

    设f（x-1）=x2，则f（x+1）=（）


    正确答案:x2+4x+4

  • 第8题：

    单选题
    设y＝f[（2x－1）/（x＋1）]，f′（x）＝ln（x1/3），则dy/dx＝（　　）。
    A

    ln[（2x－1）/（x－1）]/（x＋1）2

    B

    ln[（2x＋1）/（x＋1）]/（x＋1）2

    C

    ln[（2x＋1）/（x＋1）]/（x－1）2

    D

    ln[（2x－1）/（x＋1）]/（x＋1）2


    正确答案： D
    解析：
    令u＝（2x－1）/（x＋1），则u′（x）＝3/（x＋1）2。dy/dx＝f′（u）·u′（x）＝ln（u1/3）·3/（x＋1）2＝ln[（2x－1）/（x＋1）]/（x＋1）2。

  • 第9题：

    单选题
    若函数z＝f（x，y）满足∂2z/∂y2＝2，且f（x，1）＝x＋2，fy′（x，1）＝x＋1，则f（x，y）＝（　　）。
    A

    y2＋（x－1）y＋2

    B

    y2＋（x＋1）y＋2

    C

    y2＋（x－1）y－2

    D

    y2＋（x＋1）y－2


    正确答案： D
    解析：
    因为∂2z/∂y2＝2，等式两边对y积分得，fy′（x，y）＝2y＋φ1（x）。
    又fy′（x，1）＝x＋1，则φ1（x）＝x－1。
    故fy′（x，y）＝2y＋x－1。两边再对y积分得f（x，y）＝y2＋xy－y＋φ2（x）。
    又f（x，1）＝x＋2，故φ2（x）＝2。
    故f（x，y）＝y2＋xy－y＋2。

  • 第10题：

    单选题
    设（d／dx）f（x）=g（x），h（x）=x2，则（d／dx）f［h（x）]等于：（）
    A

    g（x2）

    B

    2xg（x）

    C

    x2g（x2）

    D

    2xg（x2）


    正确答案： D
    解析： 暂无解析

  • 第11题：

    填空题
    设y＝f[（2x－1）/（x＋1）]，f′（x）＝ln（x1/3），则dy/dx____。

    正确答案： ln[(2x-1)/(x+1)]/(x+1)2
    解析：
    令u＝（2x－1）/（x＋1），则u′（x）＝3/（x＋1）2。dy/dx＝f′（u）·u′（x）＝ln（u1/3）·3/（x＋1）2＝ln[（2x－1）/（x＋1）]/（x＋1）2。

  • 第12题：

    单选题
    设f(x)=x(x-1)（x-2），则方程f'(x)=0的实根个数是：
    A

    3

    B

    2

    C

    1

    D

    0


    正确答案： A
    解析：

  • 第13题：

    设函数f(x)=1／x＋1,则f(f(x))=()。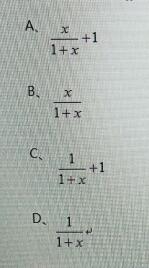


    答案：A

    解析：由函数f(x)=1/x+1，

    令f(x)=t

    则f(f(x))=f(t)=1/t+1=1/(1/x+1)+1=x/(1+x)+1，故选A。

  • 第14题：

    设f'（lnx）=1+x，则f（x）等于：


    答案：C
    解析：
    提示：设lnx=t，得f'（t）=1+et形式，写成f'（x）=1+ex，积分。

  • 第15题：

    设f(x)是连续函数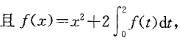， 则f(x)=
    A. x2 B. x2-2 C 2x D. x2 -16/9


    答案：D
    解析：

  • 第16题：

    设f(x)函数在[0,+∞)上连续，则f(x)是：
    A. xe-x
    B.xe-x-ex-1
    C. ex-2
    D. (x-1)e-x


    答案：B
    解析：
    提示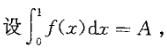：于是原题化为f(x)=xe-x+Aex......①

    分别计算出定积分值：

  • 第17题：

    设函数f(x)＝ex，则．f(x－a)·f(x＋a)＝（　　）

    A.f(x2－a2)
    B.2f(x)
    C.f(x2)
    D.f2(x)

    答案：D
    解析：

  • 第18题：

    设f'(lnx) = 1 + x，则f(x)等于（ ）。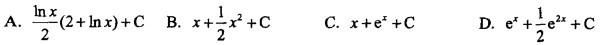


    答案：C
    解析：
    提示：令t =lnx,再两边积分。

  • 第19题：

    设（d／dx）f（x）=g（x），h（x）=x2，则（d／dx）f［h（x）]等于：（）

    • A、g（x2）
    • B、2xg（x）
    • C、x2g（x2）
    • D、2xg（x2）

    正确答案:D

  • 第20题：

    单选题
    设y＝f[（2x－1）/（x＋1）]，f′（x）＝ln（x1/3），则dy/dx（　　）。
    A

    ln[（2x－1）/（x＋1）]（x＋1）

    B

    ln[（2x－1）/（x＋1）]/（x＋1）2

    C

    ln[（2x－1）/（x＋1）]（x＋1）2

    D

    ln[（2x－1）/（x＋1）]/（x＋1）


    正确答案： D
    解析：
    令u＝（2x－1）/（x＋1），则u′（x）＝3/（x＋1）2。dy/dx＝f′（u）·u′（x）＝ln（u1/3）·3/（x＋1）2＝ln[（2x－1）/（x＋1）]/（x＋1）2。

  • 第21题：

    填空题
    设f（x-1）=x2，则f（x+1）=（）

    正确答案： x2+4x+4
    解析： 暂无解析

  • 第22题：

    填空题
    设f（x）是可导函数，且f′（x）＝sin2[sin（x＋1）]，f（0）＝4，f（x）的反函数是x＝φ（y），则φ′（4）＝____。

    正确答案： 1/sin2(sin1)
    解析：
    φ′（4）＝1/f′（0）＝1/sin2（sin1）。

  • 第23题：

    单选题
    设函数f（x）＝x2（x－1）（x－2），则f′（x）的零点个数为（　　）。
    A

    0

    B

    1

    C

    2

    D

    3


    正确答案： A
    解析：
    函数f（x）＝x2（x－1）（x－2），f（0）＝f（1）＝f（2）＝0，由罗尔定理可知，至少有ξ1∈（0，1）、ξ2∈（1，2）使得f′（ξ1）＝0，f′（ξ2）＝0，即f′（x）至少有两个零点。又函数f（x）是四次多项式，故f′（x）是三次多项式，三次方程f′（x）＝0的实根不是一个就是三个，故f′（x）有三个零点。

相关内容